Лекции / Лекция 6

Лекция 6

Вычислим производящую функцию для последовательности. Производящая функция p(Z) для последовательности чисел p₀, p₁, p₂,… задаётся следующим образом:

p(Z)=

где Z– некоторый параметр и |Z|<1. Тогда

Данная производящая функция соответствует последовательности:

,

Значение p_о найдем из условия нормировки:

.

Имеем:

Все данные соотношения справедливы, если Это условие называется условием стационарности процесса.

Найдем оперативные характеристики системы.

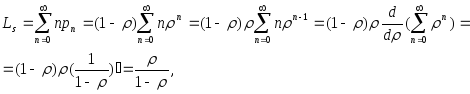
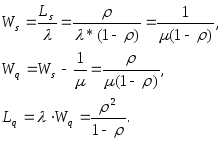
Как видно из всех этих соотношений, с ростом коэффициента все оперативные характеристики системы ухудшаются.

Коэффициент называется пропускной способностью системы или коэффициентом использования системы.

В рассматриваемой модели не учитывалась дисциплина очереди, т.е. среднее время пребывания в очереди получилось независимым от ее дисциплины. В случае, когда требуется вычислить статистические характеристики системы, касающиеся времени пребывания в системе, необходимо знать распределения вероятностей времени пребываний требований в системе. Здесь уже важна дисциплина очереди.

Модель (M/M/1):(FIFO//)

Обозначим через время пребывания в системе очередного требования (от момента прибытия до момента завершения обслуживания).

Пусть прибывающее требование обнаруживает в системе n требований, прибывших перед ним и еще не обслуженных. Новое требование будет (n +1).

В этом случае = t₁' + t₂ + t₃ + ... + t_n+1 .

t₁' - время, необходимое для того, чтобы завершилась обработка первого требования, которое уже находится в узле обслуживания.

t₂,t₃,… – время, в течение которого будут обрабатываться в узле обслуживания второе, третье и т.д. требования.

Обозначим через w( /n+1) условную плотность распределения случайной величины, когда перед только что поступившим требованием в системе уже находятся n требований.

В рассмотренной нами системе массового обслуживания величины t₂,t₃ и т.д. подчиняются экспоненциальному закону распределения с параметром . Исходя из свойства экспоненциального закона распределения (свойство отсутствия памяти), t₁' подчиняется тому же закону распределения.

Т.о., время есть сумма (n+1) независимых случайных величин, каждая из которых подчиняется экспоненциальному закону распределения с параметром . Т.е. подчиняется распределению Эрланга с (n+1) степенями свободы и параметром . Его закон распределения задаётся функцией плотности вероятности:

.

Найдем безусловную плотность распределения случайной величины .

.

Т.о., время пребывания требования в системе подчиняется экспоненциальному закону распределения с параметром (1-).

- математическое ожидание.

Модель (M/M/1):(GD/N/)

Данная модель отличается от предыдущей тем, что здесь количество требований, находящихся в системе, ограничивается величиной N (длина очереди не может превышать (N –1)). Это означает, что очередное требование будет отвергнуто системой, если в ней уже находится N требований. В результате этого эффективная частота поступлений требований становится меньше частоты поступления требований ,.,, , нуждающихся в обслуживании:

.

Для данной модели условие стационарности () уже необязательно. Уравнения для p_n(t) (n = 0,...,N-1) остаются такими же, как и на прошлой модели, а для N они изменяются:

Отсюда получаем следующую систему соотношений, проводя подобное преобразование для стационарной модели.

Найдем производящую функцию:

Поскольку в системе не может находиться более чем N требований, то при n>N все p_n = 0, т.е. мы можем заменить конечную сумму на бесконечную:

Для данной производящей функции мы можем найти исходную последовательность:

,

для функции

Значение p_о найдем из условия нормировки:

Здесь при вычислении суммы требования ρ<1 необязательно. В случае, если ρ = 1, то мы получаем:

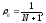
В случае ρ ≠ 1, имеем:

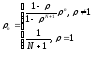
Найдем оперативные характеристики системы:

при ρ 1

при ρ =1

.

Для того, чтобы найти остальные оперативные характеристики (L_q, W_s, W_q), необходимо вычислить _эфф - частоту вхождения требования в СМО.

Для этого надо вычислить вероятность того, что очередное требование войдет в систему. Это произойдет, если число требований в ней:

Пример.

Интенсивность поступления требований = 5 (требований/мин). Среднее время обработки одного требования – 10 сек, закон распределения времени– экспоненциальный. Следовательно, интенсивность обслуживания = 6 (требований/мин). Память, отведенная под хранение очереди требований, позволяет сохранять только 5 требований. Если очередь уже составляет 5 требований, то очередное поступившее требование теряется. Таким образом, мы имеем модель (М/M/1) : (GD/6/).

Рассмотрим, сколько требований не будет обслужено из-за ограниченности памяти, отводимой под очередь. Для этого необходимо рассмотреть разницу:

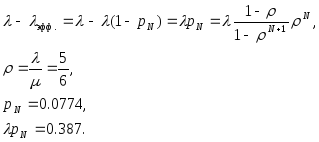
Таким образом, в среднем за 1 час работы системы не будут обслужены 60*0.387 24 требования.

Определим среднее время пребывания сообщения в системе. Согласно формулам, приведенным ранее, имеем L_s 9.2, _эфф. = 4.613, W_s = L_s/_эфф. = 0.496.

Для системы без ограничения на количество требований время W_s равно 1 мин.