Лекции / Лекция 9

Лекция 9

Модель (M_i/M/1):(NPRP//)

В данной модели предполагается, что имеются различные пуассоновские потоки входных требований с разными приоритетами. Считаем, что они имеют параметры _i.

Время обслуживания требований из любого потока подчиняется экспоненциальному закону распределения с параметром .

Введем обозначения:

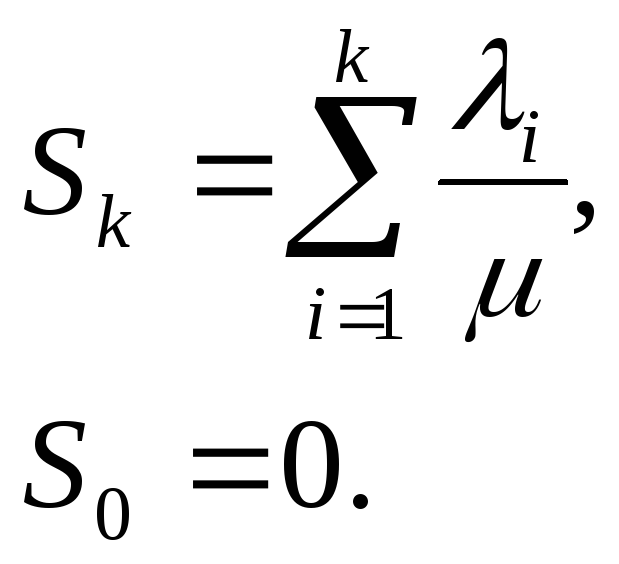
Условие стационарности– все S_k<1.

Справедливы следующие формулы:

Методы понижения дисперсии

Методы понижения дисперсии основаны на замене простой случайной выборки более совершенной выборкой. При этом применяются специальные выборочные процедуры, которые приводят к оценке интересующей величины с тем же математическим ожиданием, но с меньшей дисперсией.

Стратифицированные выборки

Сформулируем основные методы стратификации на примере. Предположим, что мы хотим оценить  - величину среднего потребления некоторой группы населения. Для этого мы возьмем выборку из n индивидуумов этой группы. Простой оценкой среднего значения µ служит величина:

здесь x_i - потребление i-того случайно выбранного индивидуума.

При этом – несмещенная оценка с дисперсией ²/n, где ² - дисперсия индивидуального наблюдения x_i, (i=1,2,…,n).

В стратифицированной выборке мы измеряем, помимо интересующей нас переменной x_i, дополнительную величину y_i, называемую стратифицирующей переменной. Она служит для того, чтобы отнести каждого отобранного индивидуума к одному из К классов. Эти классы формируются так, чтобы разделить область значений стратифицирующей переменной на непересекающиеся множества. Обозначим k-тый класс через ST_k.

Допустим, что в нашем примере стратифицирующая переменная - это доход. Положим, что индивидуум с потреблением равным x принадлежит классу k, если его доход y принадлежит слою ST_k. Для стратификации нам необходимо знать вероятности p_k

.

Мы можем выбрать n_k индивидуумов с доходами, принадлежащими классу ST_k, а затем оценить среднее значение  с помощью стратифицирующей оценки

где – оценка среднего в k-том слое;

x_ki– i-тое наблюдение в k-том слое.

Стратифицированная оценка будет несмещенной:

.

Дисперсия стратифицируемой выборки будет:

,

_k² - дисперсия в k-том слое, то есть дисперсия x_ki.

Если истинную дисперсию _k² заменить ее несмещенной оценкой:

,

то получим несмещенную оценку дисперсии отклика

.

Для заданной надежности (1-) доверительный интервал будет:

,

где z_/2 берется из таблицы нормального распределения. Если же число наблюдений в каждом слое невелико, то величина z_/2 заменяется на t_, которое берется из таблицы распределения Стьюдента с числом степеней свободы

.

Рассмотрим дисперсию стратифицированной выборки . Если мы будем брать число наблюдений n_k в каждом слое k пропорциональным вероятности: n_k=np_k, то будем иметь пропорциональную стратифицированную выборку. Дисперсия ее оценки:

.

Сравним ее с дисперсией простой выборки:

.

Мы можем оценить ² следующим образом:

Будем считать, что n_k принимает большое значение:

n -1  n, n_k -1  n_k.

Тогда:

Разделив обе части равенства на n и считая оценки за сами величины, получим:

Таким образом, стратификация полезна, когда средние различных слоев _k не все равны между собой. Средние значения _k отличаются, если интересующая нас переменная x зависит от стратифицирующей переменной y. Это означает, что x и y коррелируют между собой. Причем желательна сильная корреляция. Кроме того, для стратификации нам необходимо знать вероятности p_k распределения стратифицирующей переменной.