Лекции / Лекция 8

Лекция 8

Анализ функционирования автоматизированных систем методами теории массового обслуживания

Предполагается проектирование системы реального времени. Ее особенностью является необходимая периодичность снятия копий текущего состояния с тем, чтобы после сбоя можно было восстановить систему. Сообщение поступает в систему, и результат изменения состояния системы после поступления каждого сообщения фиксируют на внешнем магнитном носителе. Он используется в случае необходимости восстановления системы после сбоя. В результате анализа потока сообщений было выяснено, что он является пуассоновским с интенсивностью = 5 сообщений/мин. На систему налагаются следующие требования:

• время реакции системы для всех сообщений не должно превышать 10сек.

tp10

• технологические перерывы, связанные со снятием копий состояния системы должны быть не чаще 1 раза в 2 часа.

1. Требование к надежности аппаратного и программного обеспечения. Можно предположить, что время между сбоями в работе системы является случайной величиной с экспоненциальным законом распределения:

.

Т.е. среднее время между сбоями (математическое ожидание данной случайной величины) есть 1/. Необходимо найти значение параметра . Он будет определять надежность технических средств нашей системы.

Для этого необходимо решить уравнение, описывающее вероятность того, что сбой произойдет не позже чем в течение двух часов.

, где - величина близкая к нулю

Решим уравнение:

Если задать вероятность = 0.005, то = 0.025, а 1/ = 40 часов.

Если = 0.2,то = 0.11 , 1/ = 9 часов.

2. Определим объем сообщений, которые будут фиксироваться на магнитном носителе в течение часа. Число сообщений Z– есть случайная величина, подчиняющаяся пуассоновскому закону распределения. Для определения объема сообщений необходимо найти минимальное число S, удовлетворяющее уравнению:

, где – величина близкая к единице.

Для случайной величины, подчиняющейся закону распределения Пуассона с параметром , для больших значений k справедлива следующая приближенная формула:

Ф(х) – функция распределения нормальной случайной величины:

Перейдем к нашему случаю.

Из таблиц распределения находим:

Таким образом, можно считать, что с вероятностью 0.95 в течение часа придет до 328 сообщений.

3. Будем считать, что время обработки одного сообщения есть случайная величина, подчиняющаяся экспоненциальному закону распределения. Нам необходимо найти значение параметра такое, чтобы время реакции для каждого сообщения было не более 10сек. Если мы будем строить нашу систему реального времени, то время пребывания сообщения в системе есть случайная величина с плотностью распределения:

Время пребывания сообщения в системе, есть время реакции системы на сообщение.

Таким образом, нужно решить уравнение:

.

Решаем уравнение:

Среднее время реакции при такой интенсивности:

.

Длина очереди при этом:

.

Если мы откажемся от очереди, то перейдем к модели (M/M/1):(GD/1/).

В этом случае

- вероятность того, что в системе не будет ни одного сообщения.

- вероятность того, что в системе будет находиться одно сообщение.

Определим, сколько сообщений не будут обслуживаться (будут потеряны), если мы откажемся от хранения очереди в системе.

Для этого необходимо вычислить разницу _эфф.

.

Т.е. в среднем не будут обслуживаться 0.9 сообщений/мин.

4. Определим длину очереди, хранимой в системе, достаточную для того, чтобы потери составляли не более, чем 0.01 сообщений/мин. Необходимо найти значение параметра N в модели (М/М/1):(GD/N/) такое, чтобы

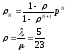
Имеем уравнение:

.

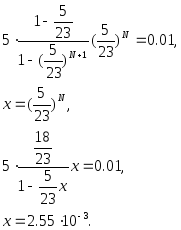
Т.о., если число сообщений, хранимых в очереди, будет равно 3, то требования на потери будут соблюдаться.

5. Когда прекращать прием новых сообщений. Для определения времени прекращения мы можем использовать модель чистой гибели. При этом будем исходить из того, что перед прекращением приема в системе находится максимально возможное число сообщений, т.е. имеет место равенство:

.

Здесь q_N(t) - вероятность того, что за время t все N сообщений будут обслужены.

Для = 0.95 мы получим уравнение: