
- •Кафедра высшей математики
- •Порядок выполнения контрольных работ
- •Рекомендуемая литература
- •Справочный материал
- •Указания к выполнению контрольной работы 1
- •Примеры решения задач
- •Контрольная работа 1
- •Указания к выполнению контрольной работы 2
- •Примеры решения задач
- •Контрольная работа 2
- •Указания к выполнению контрольной работы 3
- •Примеры решения задач
- •Контрольная работа 3
- •Указания к выполнению контрольной работы 4
- •Примеры решения задач
- •Контрольная работа 4
- •Содержание
- •Ответственный за выпуск м.Г. Плотников Корректор г.Н. Елисеева
Указания к выполнению контрольной работы 3
Т е м а 11. Функции нескольких переменных
ЛИТЕРАТУРА:
[6], гл. XX, § 1–3, §7, §8, §10, упр. 4, 5, 8;
[7], задачи 1858, 1860, 1861, 1870, 1874, 1927, 1952, 2017, 2028, 2030, 2031, 2033;
[8], гл. VIII, § 1–5, §10–12, §14, §15, §17, упр. 1–4, 8–9, 34, 35, 47, 48.
Т е м а 12. Дифференциальные уравнения первого порядка
[6], гл. XXII, § 1–5, упр. 4, 5, 7, 8;
[7], задачи 2061, 2062, 2064, 2080, 2093, 2096, 2098, 2101, 2118, 2119;
[8], гл. XIII, § 1–5, § 7 8, упр. 1–3, 9–11, 39, 40, 57, 66.
Т е м а 13. Дифференциальные уравнения второго порядка
[6], гл. XXII, § 7–9, § 12–13, упр. 19–21, 24, 25, 27;
[7], задачи 2184, 2186, 2187–2189, 2202, 2213, 2221, 2237, 2241;
[8], гл. XIII, § 16–18, §20–24, упр. 122, 129–134, 148, 150, 155.
Примеры решения задач
Пример
34. Задана
функция двух переменных
![]() .
Найти: 1) частные производные второго
порядка
.
Найти: 1) частные производные второго
порядка
![]() ,
,
![]() ;
2) смешанные частные производные
;
2) смешанные частные производные
![]() ,
,
![]() ;
3) градиент функции
;
3) градиент функции
![]() в точке
в точке
![]() .
.
Решение. 1). Найдем частную производную функции по переменной , при этом будет считаться постоянной величиной. Имеем:
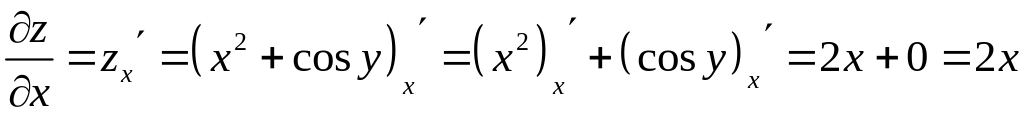 .
.
Чтобы найти частную производную второго порядка , продифференцируем первую частную производную еще раз по переменной , при этом будет по-прежнему считаться постоянной величиной. Находим:
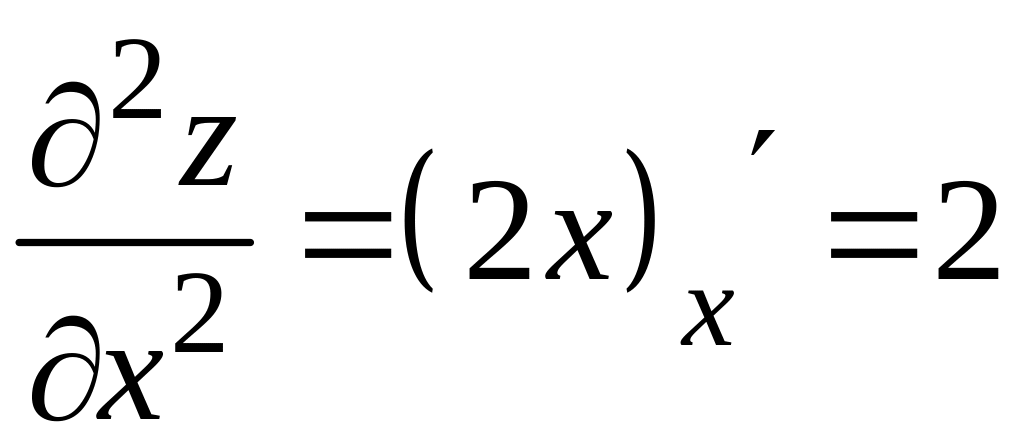 .
.
Найдем частную производную функции по переменной , при этом будет считаться постоянной величиной. Имеем:
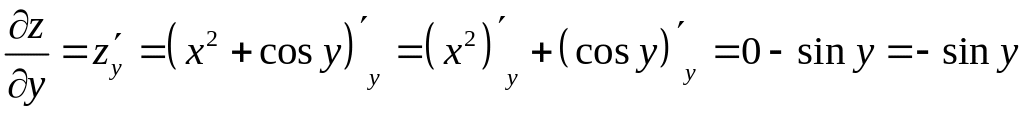 .
.
Чтобы найти частную производную второго порядка , продифференцируем первую частную производную еще раз по переменной , при этом будет по-прежнему считаться постоянной величиной. Находим:
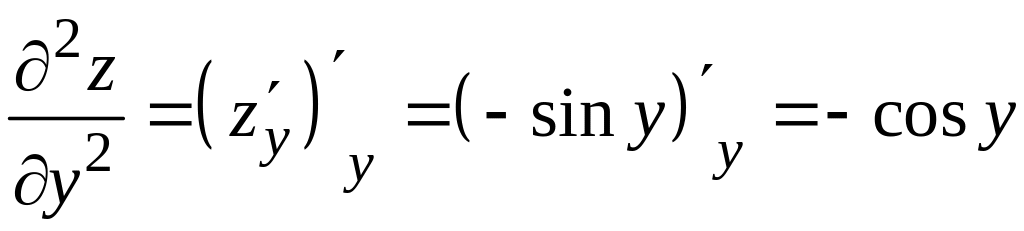 .
.
2)
Для нахождения смешанных частных
производных продифференцируем частную
производную
![]() по переменной
,
а частную производную
по переменной
,
а частную производную
![]() по переменной
.
Получим
по переменной
.
Получим
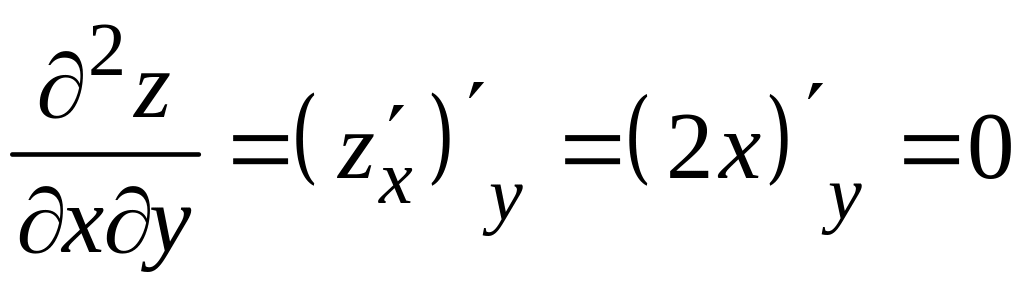 ,
,
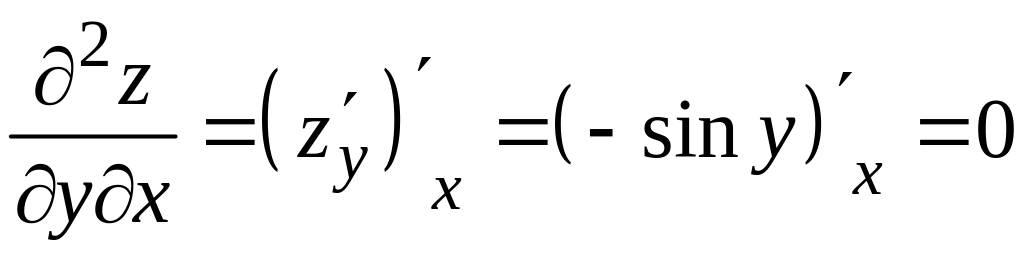 .
.
3) Вычислим значения частных производных первого порядка функции в точке :
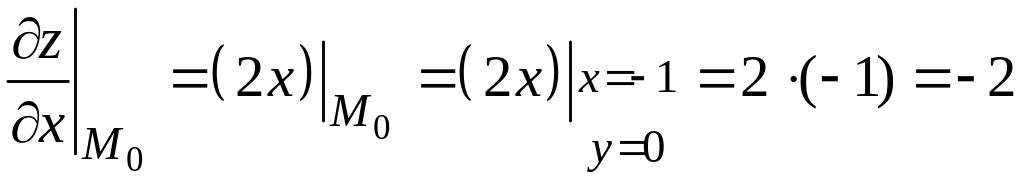 ;
;
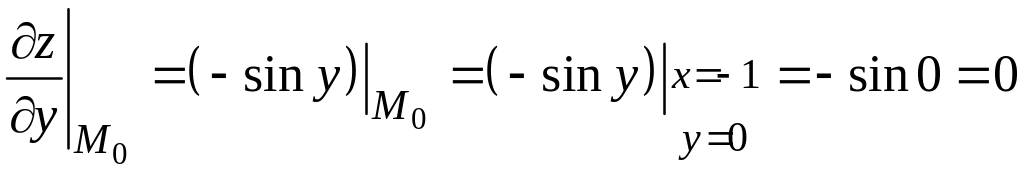 .
.
Тогда
градиент функции
в точке
есть вектор с
координатами
![]() .
.
Пример
35. Задана
функция двух переменных
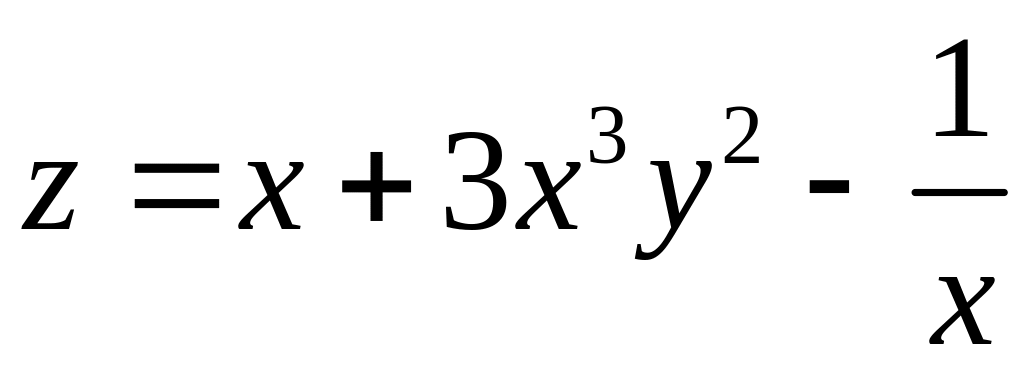 .
Найти: 1) частные производные второго
порядка
,
;
2) смешанные частные производные
,
;
3) градиент функции
в точке
.
Найти: 1) частные производные второго
порядка
,
;
2) смешанные частные производные
,
;
3) градиент функции
в точке
![]() .
.
Решение. 1). Найдем частную производную функции по переменной , при этом будет считаться постоянной величиной. Имеем:
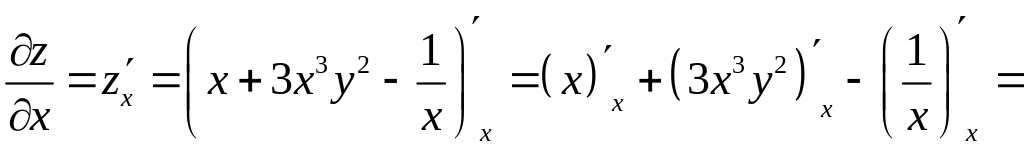
 .
.
Чтобы найти частную производную второго порядка , продифференцируем первую частную производную еще раз по переменной , при этом будет по-прежнему считаться постоянной величиной. Находим:

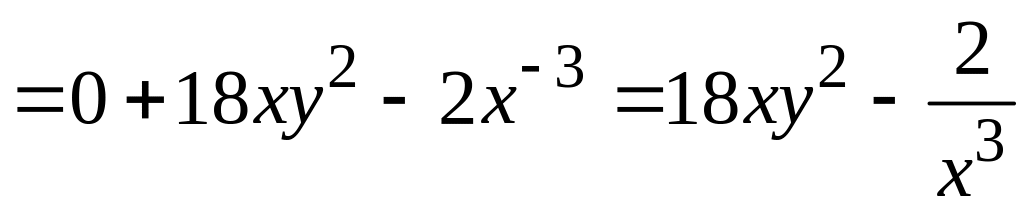 .
.
Найдем частную производную функции по переменной , при этом будет считаться постоянной величиной. Имеем:

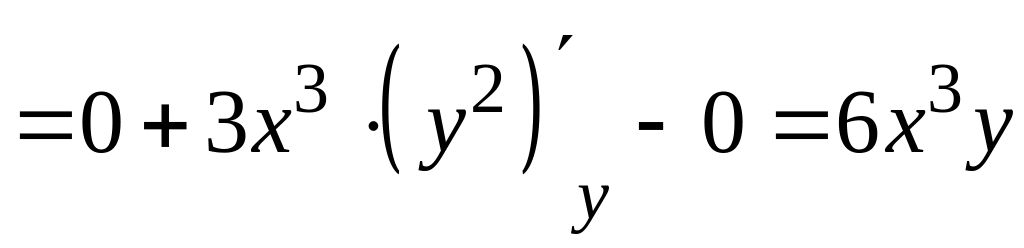 .
.
Чтобы найти частную производную второго порядка , продифференцируем первую частную производную еще раз по переменной , при этом будет по-прежнему считаться постоянной величиной. Находим:
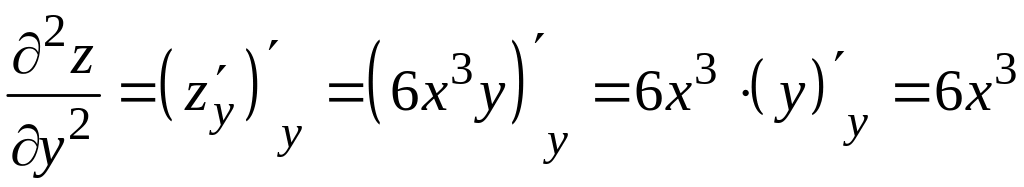 .
.
2) Для нахождения смешанных частных производных продифференцируем частную производную по переменной , а частную производную по переменной . Получим
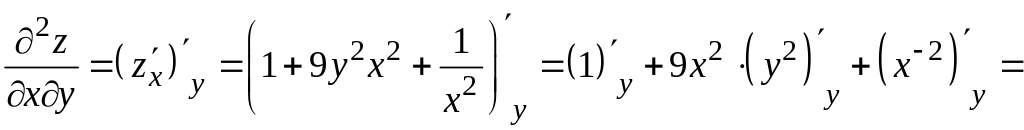
![]() ,
,
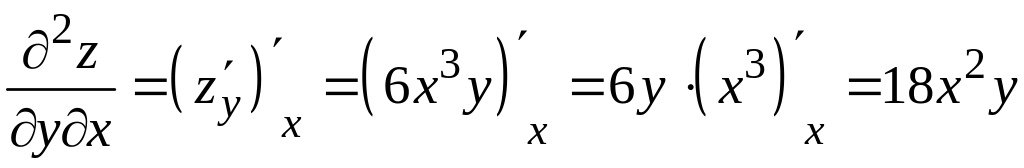 .
.
3) Вычислим значения частных производных первого порядка функции в точке :
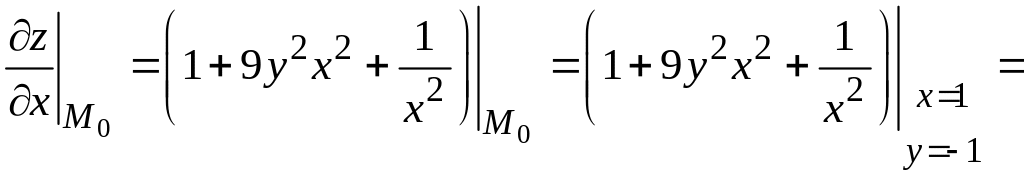
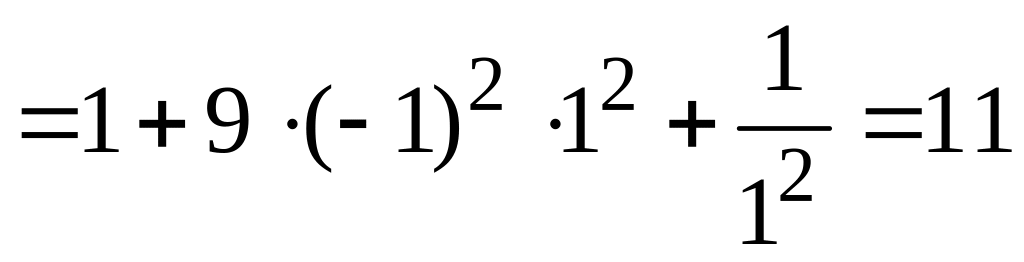 ;
;
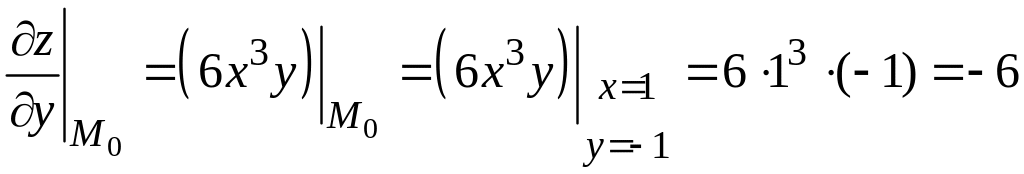 .
.
Тогда
градиент функции
в точке
есть вектор с координатами
![]() .
.
Пример
36. Задана
функция двух переменных
![]() .
Найти: 1) частные производные второго
порядка
,
;
2) смешанные частные производные
,
;
3) градиент функции
в точке
.
Найти: 1) частные производные второго
порядка
,
;
2) смешанные частные производные
,
;
3) градиент функции
в точке
![]() .
.
Решение. 1). Найдем частную производную функции по переменной , при этом будет считаться постоянной величиной. Имеем:
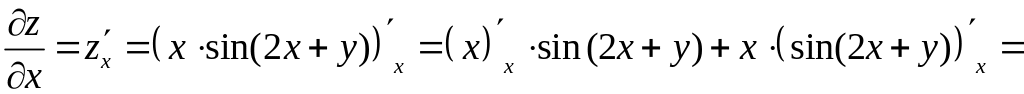
![]()
![]() .
.
Чтобы найти частную производную второго порядка , продифференцируем первую частную производную еще раз по переменной , при этом будет по-прежнему считаться постоянной величиной. Находим:
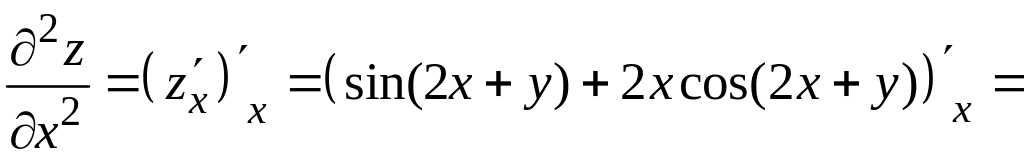
![]()
![]()
![]()
![]() .
.
Найдем частную производную функции по переменной , при этом будет считаться постоянной величиной. Имеем:

![]() .
.
Чтобы найти частную производную второго порядка , продифференцируем первую частную производную еще раз по переменной , при этом будет по-прежнему считаться постоянной величиной. Находим:
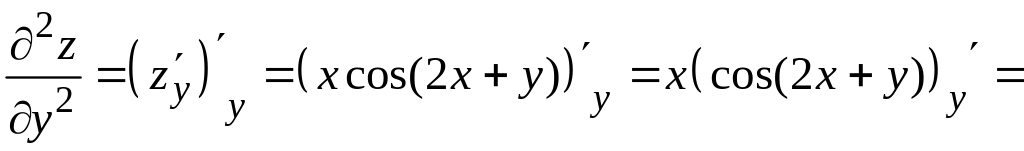
![]() .
.
2) Для нахождения смешанных частных производных продифференцируем частную производную по переменной , а частную производную по переменной . Получим
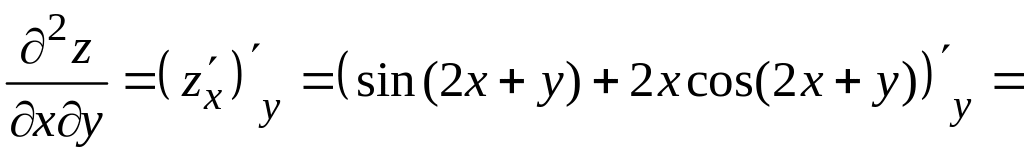
![]()
![]()
![]() ;
;

![]()
![]() .
.
3) Вычислим значения частных производных первого порядка функции в точке :

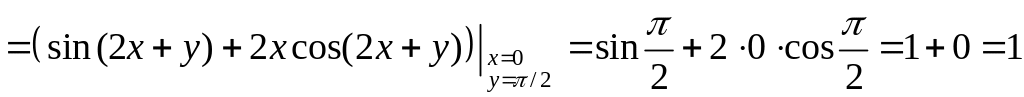 ;
;
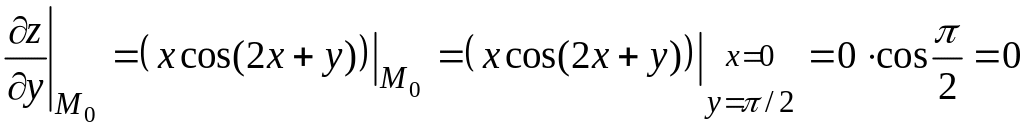 .
.
Тогда
градиент функции
в точке
есть вектор с координатами
![]() .
.
Пример
37. Задана
функция двух переменных
 .
Найти: 1) частные производные второго
порядка
,
;
2) смешанные частные производные
,
;
3) градиент функции
в точке
.
Найти: 1) частные производные второго
порядка
,
;
2) смешанные частные производные
,
;
3) градиент функции
в точке
![]() .
.
Решение. 1). Найдем частную производную функции по переменной , при этом будет считаться постоянной величиной. Имеем:
 .
.
Чтобы найти частную производную второго порядка , продифференцируем первую частную производную еще раз по переменной , при этом будет по-прежнему считаться постоянной величиной. Находим:
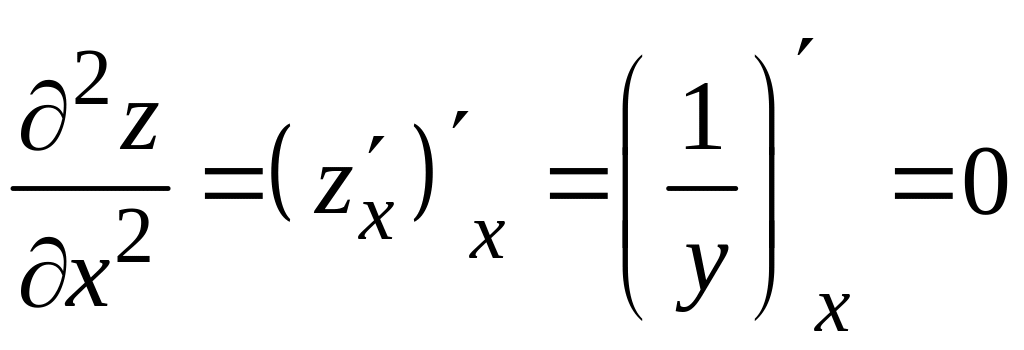 .
.
Найдем частную производную функции по переменной , при этом будет считаться постоянной величиной. Имеем:
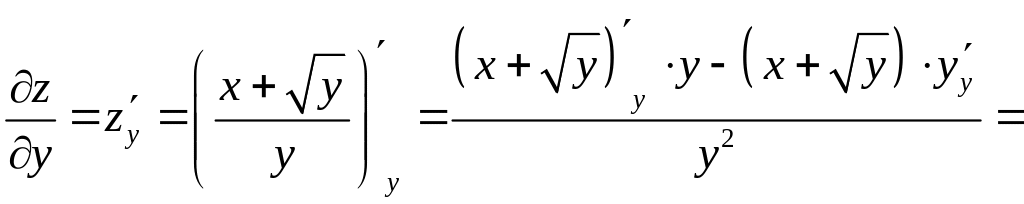
 .
.
Чтобы найти частную производную второго порядка , продифференцируем первую частную производную еще раз по переменной , при этом будет по-прежнему считаться постоянной величиной. Находим:
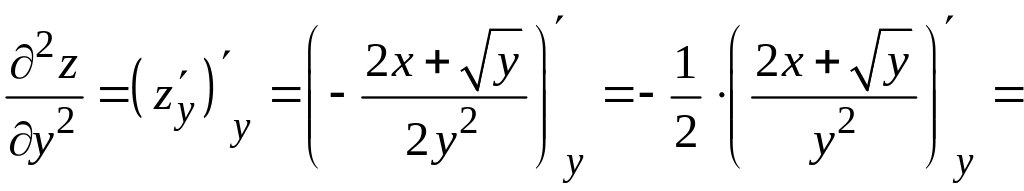
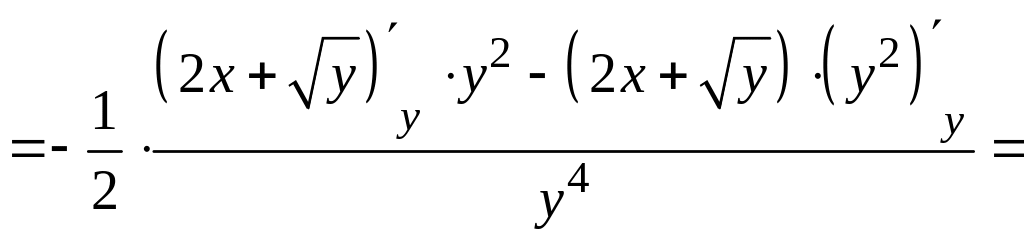
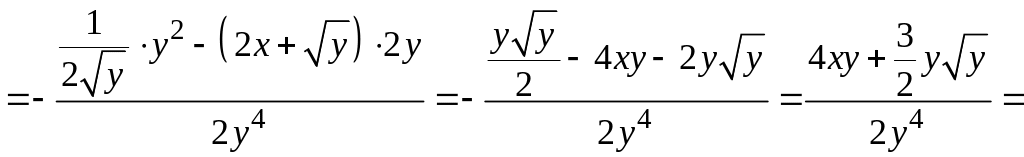
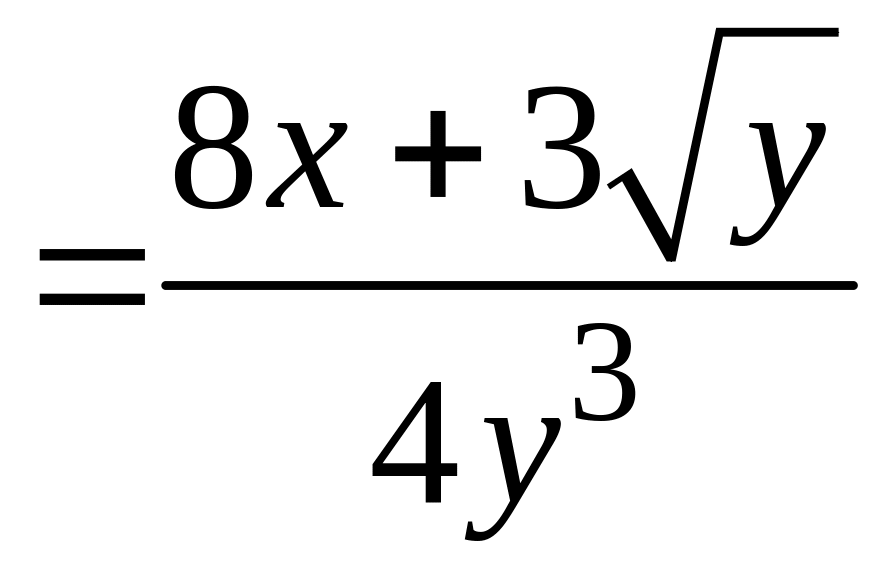 .
.
2) Для нахождения смешанных частных производных продифференцируем частную производную по переменной , а частную производную по переменной . Получим
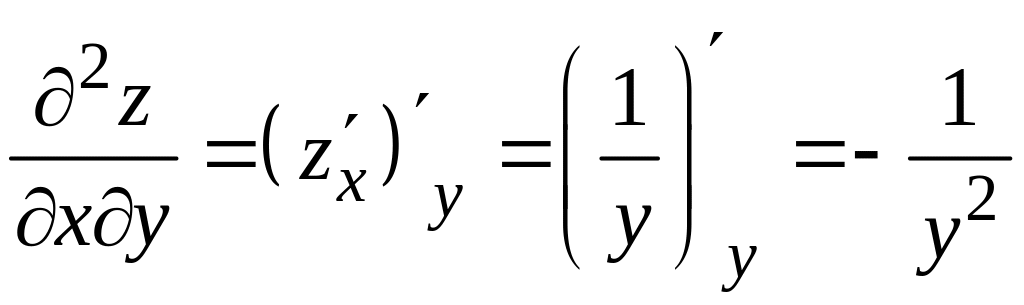 ,
,
 .
.
3) Вычислим значения частных производных первого порядка функции в точке :
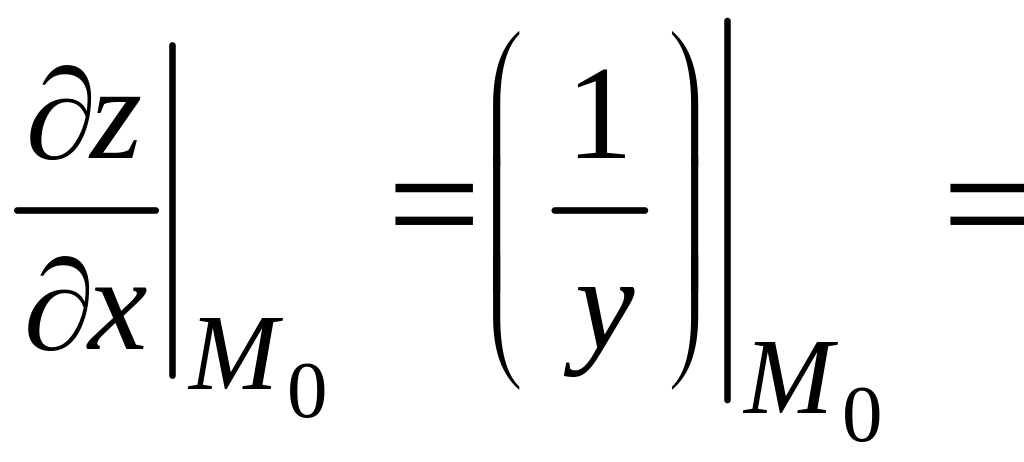
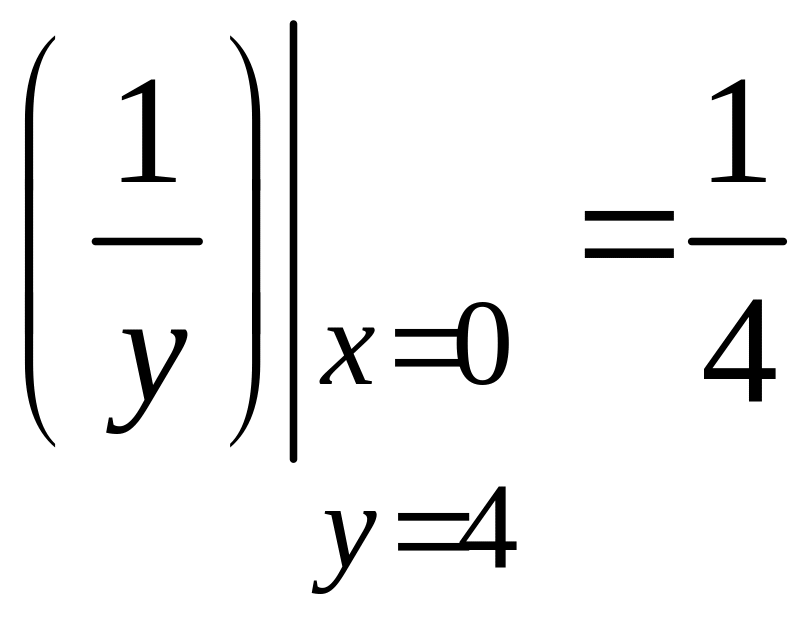 ;
;
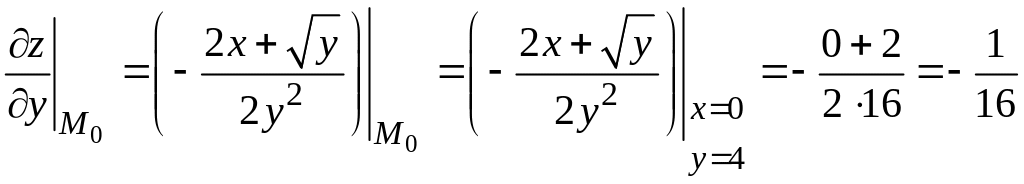 .
.
Тогда
градиент функции
в точке
есть вектор с координатами
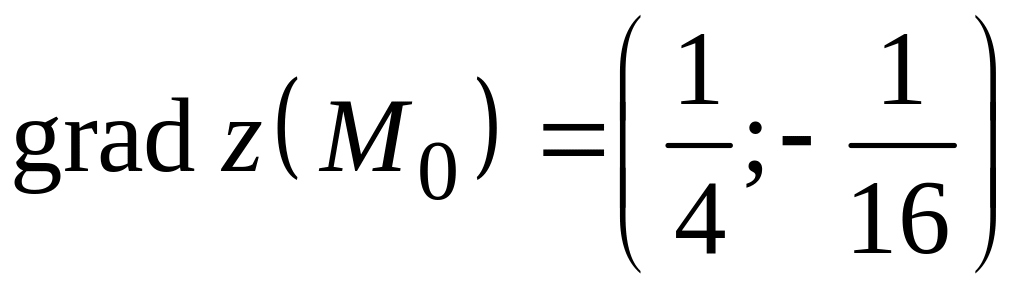 .
.
Пример
38. Исследовать
на экстремум заданную функцию двух
переменных
![]() .
.
Решение.
1) Найдем точки, подозрительные на
экстремум. Для этого вычислим частные
производные функции
![]() и
и
![]() ,
а затем решим систему
,
а затем решим систему
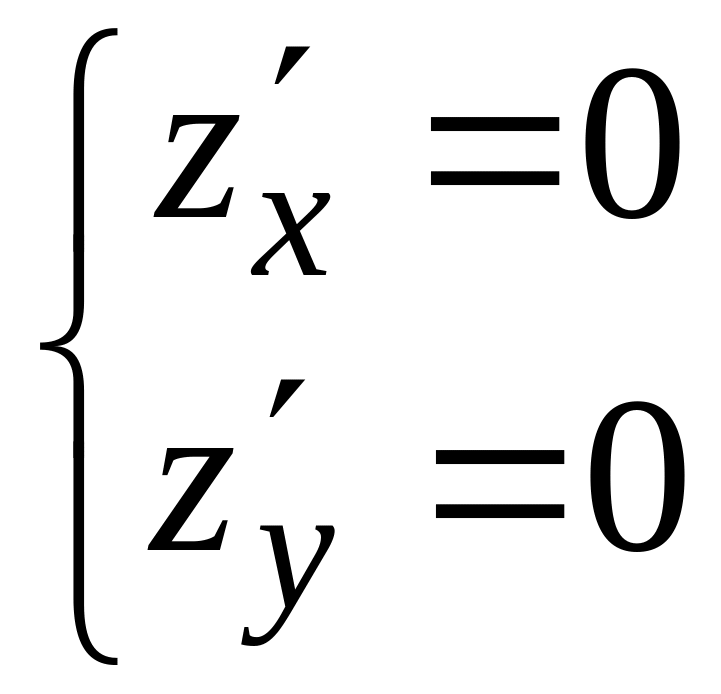 .
.
Имеем:
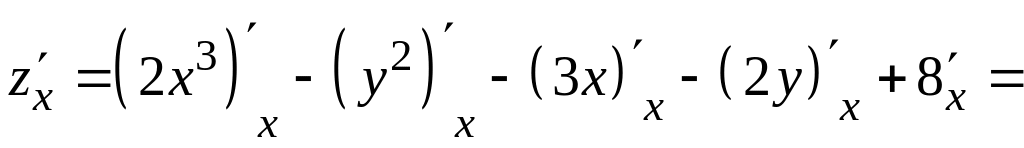
![]() ,
,
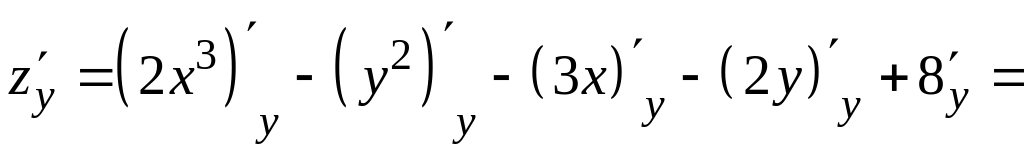
![]() .
.
Система примет вид
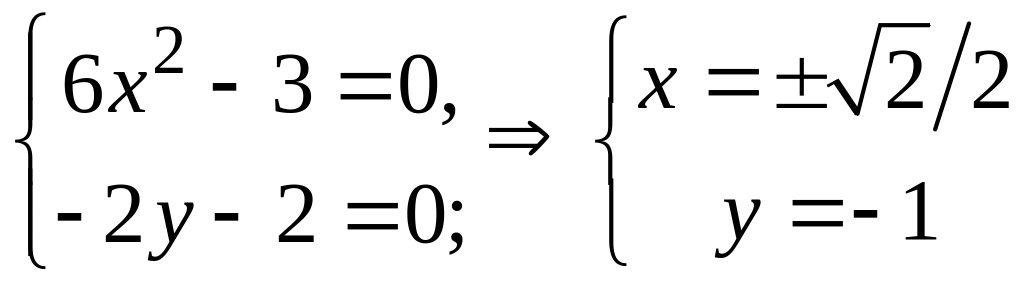 .
.
Итак,
найдены две точки, подозрительные на
экстремум:
![]() и
и
![]() .
.
2)
Выясним, есть ли в точках
![]() и
и
![]() экстремумы. Для этого вычислим в точках
и
значение выражения
экстремумы. Для этого вычислим в точках
и
значение выражения
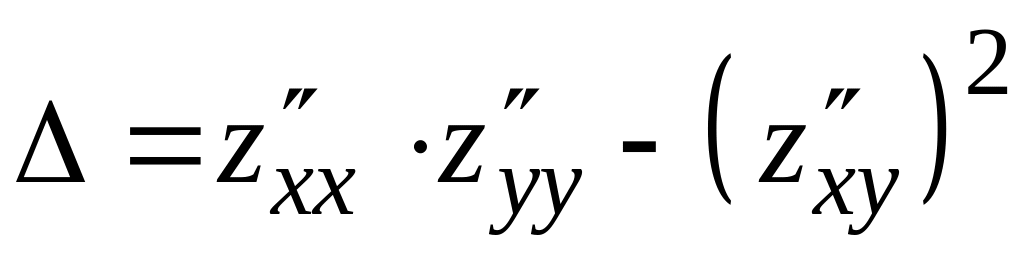 .
Находим
.
Находим
 ,
,
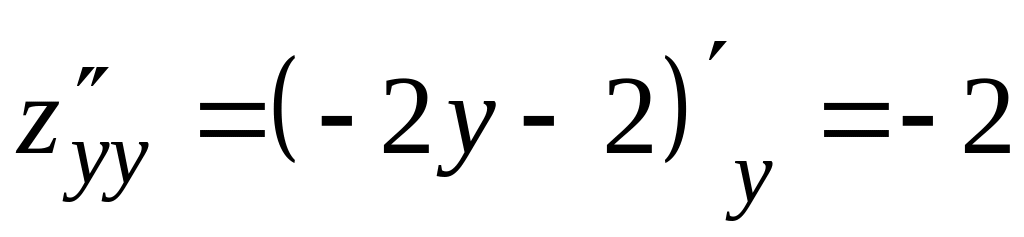 ,
,
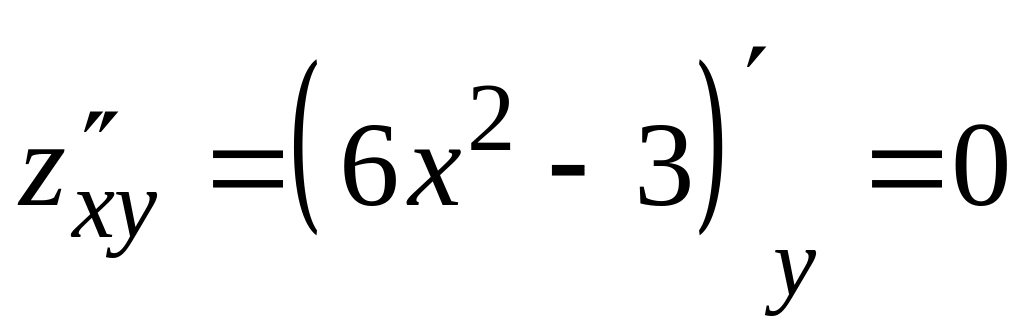 .
.
Тогда
![]() .
.
В точке :
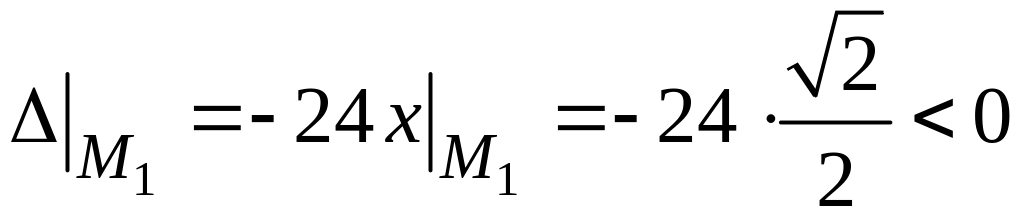 ,
,
следовательно, экстремума в точке нет.
В точке :
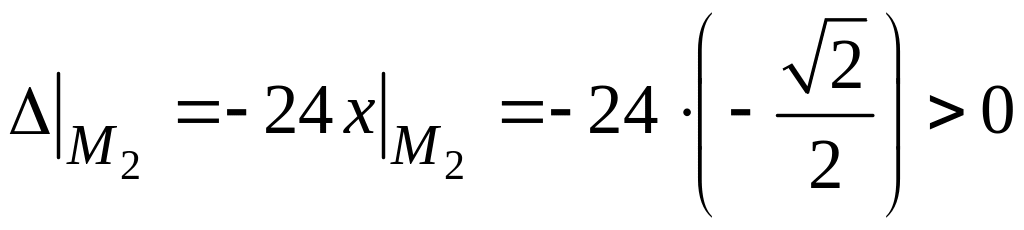 ,
,
следовательно, экстремум в точке есть, причем максимум, так как
 .
.
Тогда значение функции в точке максимума

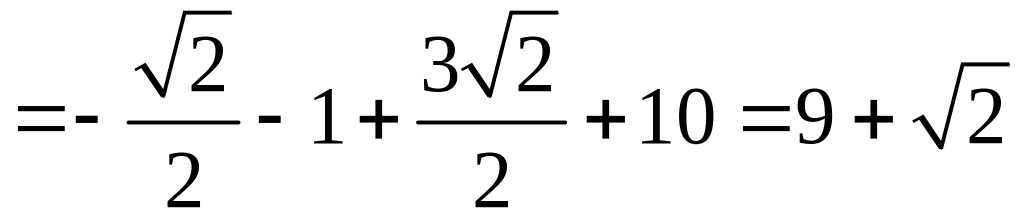 .
.
Пример
39. Исследовать
на экстремум заданную функцию двух
переменных
![]() .
.
Решение. 1) Найдем точки, подозрительные на экстремум. Для этого вычислим частные производные функции и , а затем решим систему .
Имеем:
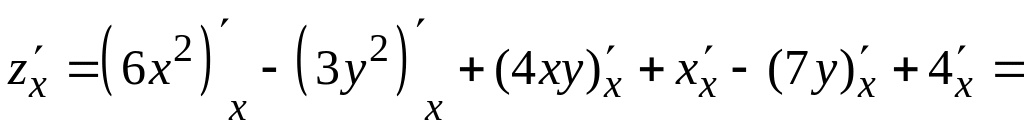
![]() ,
,
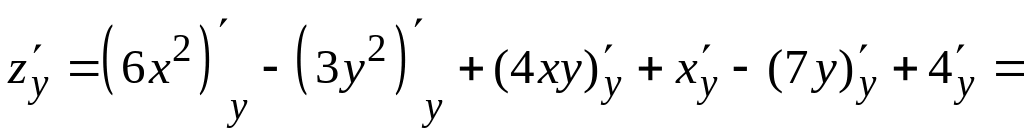
![]() .
.
Система примет вид

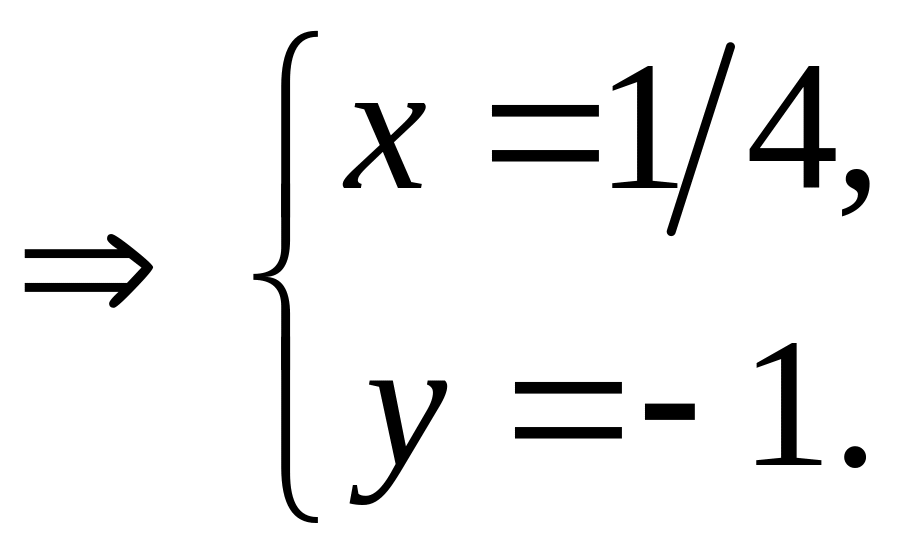
Итак,
найдена одна точка, подозрительная на
экстремум:
![]() .
.
2)
Выясним, есть ли в точке
экстремум. Для этого вычислим в точке
значение выражения
.
Находим
![]() ,
,
![]() ,
,
![]() .
Тогда
.
Тогда
![]() .
.
В
точке
:
![]() ,
следовательно, экстремума в точке
нет. Значит, функция
экстремумов не имеет.
,
следовательно, экстремума в точке
нет. Значит, функция
экстремумов не имеет.
Пример 40. Найти общее решение (общий интеграл) дифференциальных уравнений первого порядка:
а)
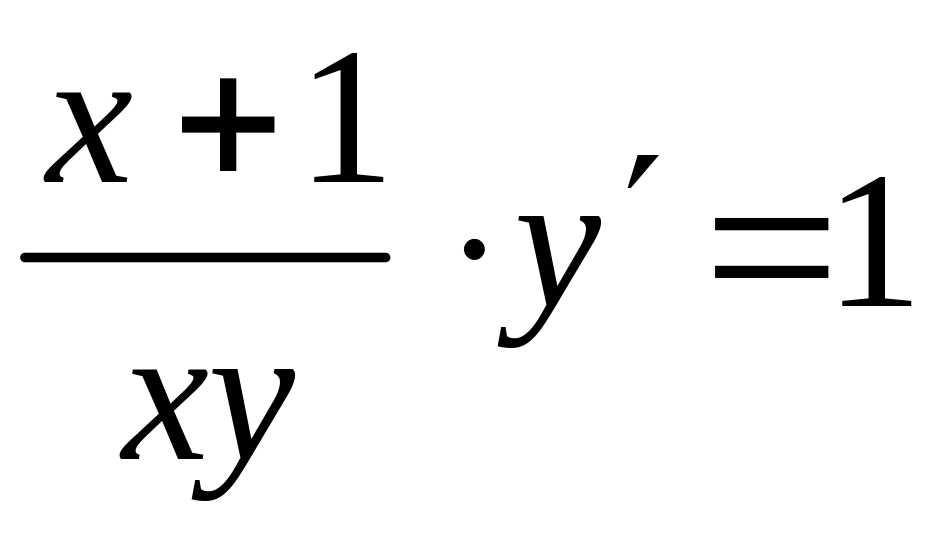 ;
б)
;
б)
![]() .
.
Решение.
а) Т.к.
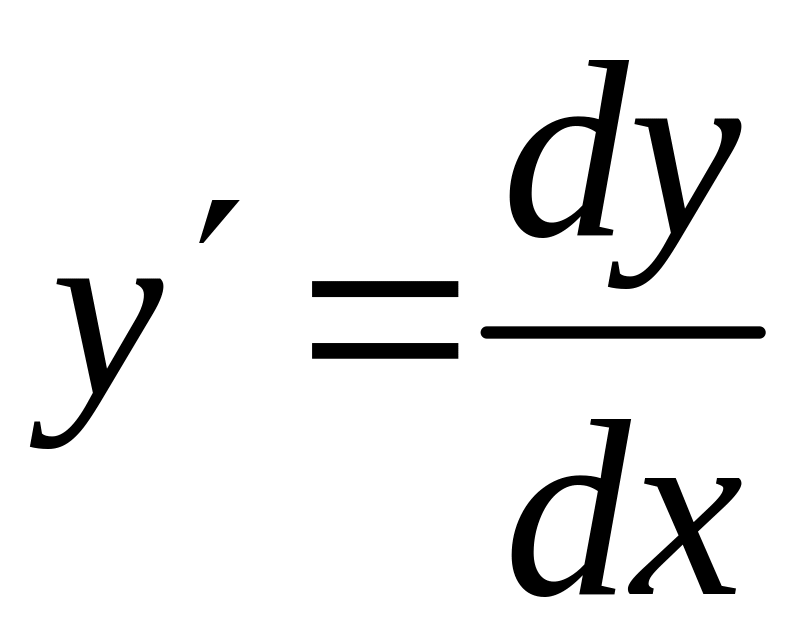 ,
то уравнение можно записать в виде
,
то уравнение можно записать в виде
 .
.
Умножим
обе части уравнения на
![]() :
:
 .
.
Данное уравнение является дифференциальным уравнением с разделяющимися переменными, т.к. оно имеет вид
![]() ,
,
где
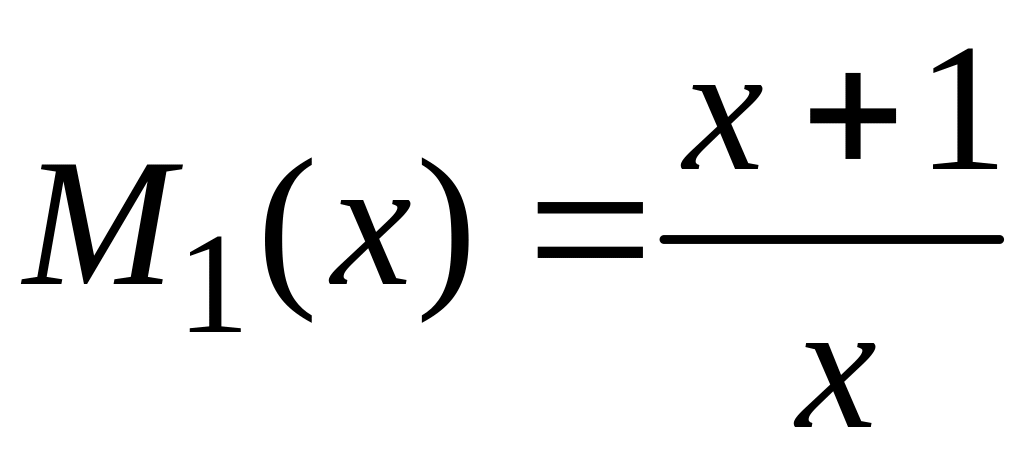 ,
,
 ,
,
![]() ,
,
![]() .
Разделим переменные. Умножив обе части
на
,
а затем поделив на
.
Разделим переменные. Умножив обе части
на
,
а затем поделив на
![]() будем иметь:
будем иметь:
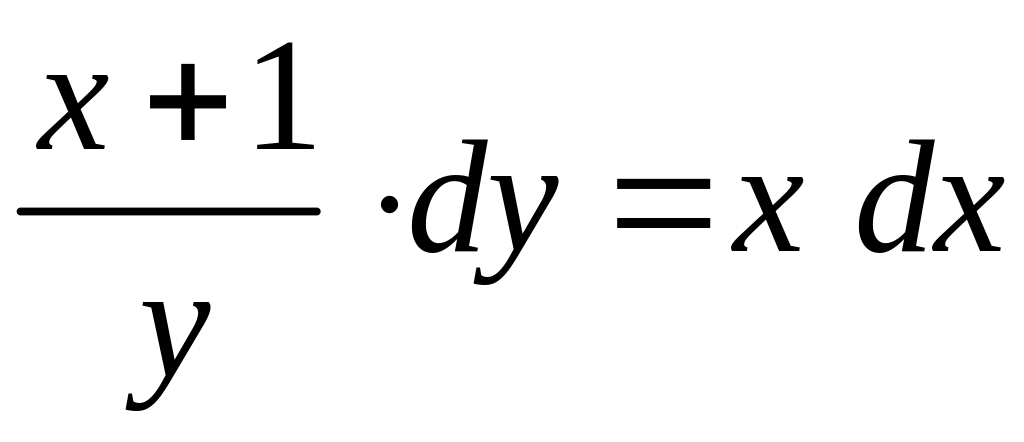 ,
,
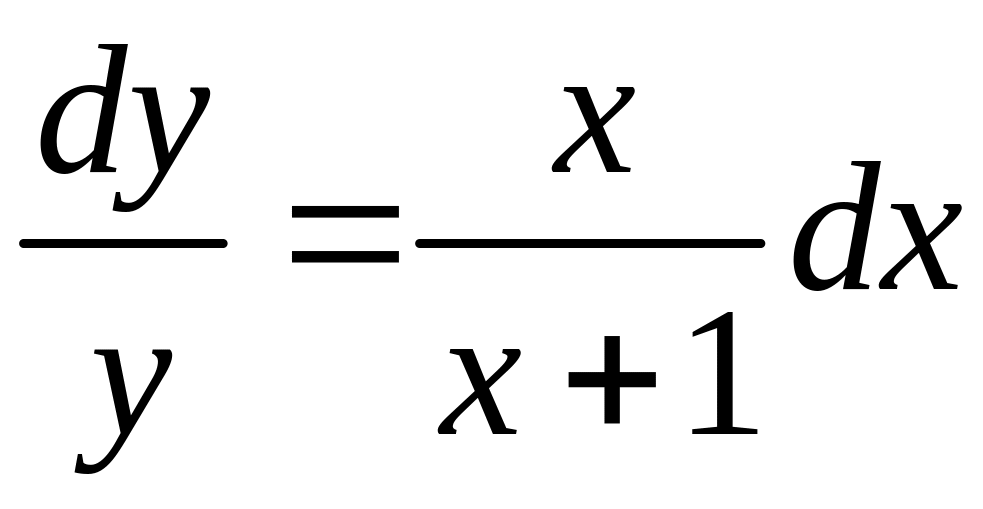 .
.
Получили дифференциальное уравнение с разделенными переменными и . Интегрируя, получим:
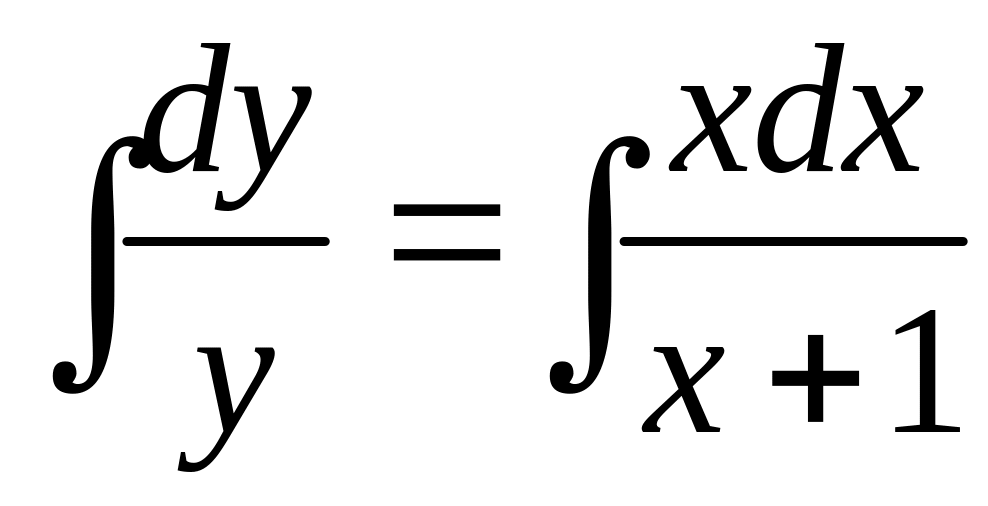 ,
,
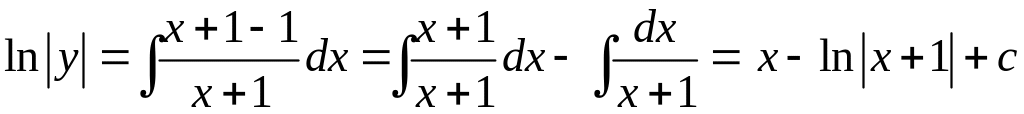 .
.
Потенцируя, находим:
![]() ,
,
 ,
,
 ,
,
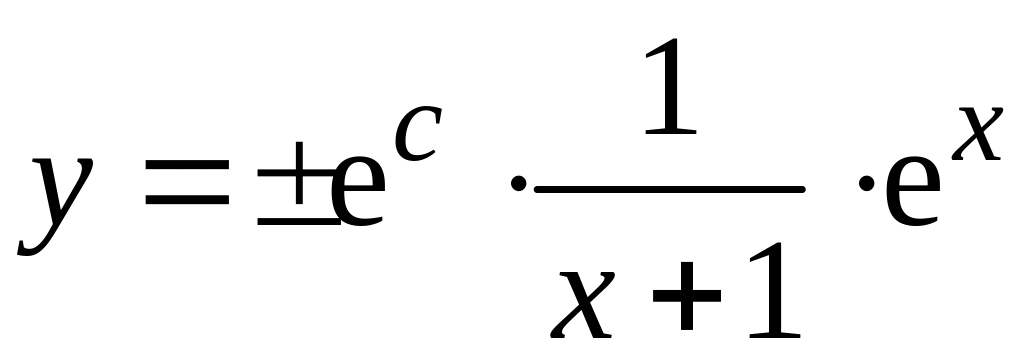 .
.
Обозначив
![]() ,
получим:
,
получим:
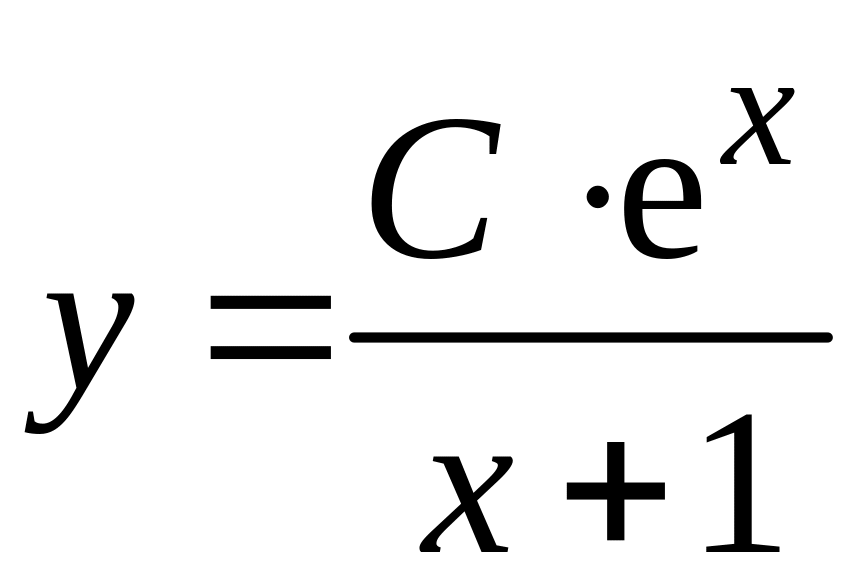 – общее решение данного дифференциального
уравнения.
– общее решение данного дифференциального
уравнения.
б) Данное уравнение является дифференциальным уравнением с разделяющимися переменными, т.к. его можно представить в виде
![]() ,
,
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Разделим обе части уравнения на
.
Разделим обе части уравнения на
![]() ,
будем иметь:
,
будем иметь:
 ,
,
 .
.
Переменные разделены, проинтегрируем обе части уравнения:
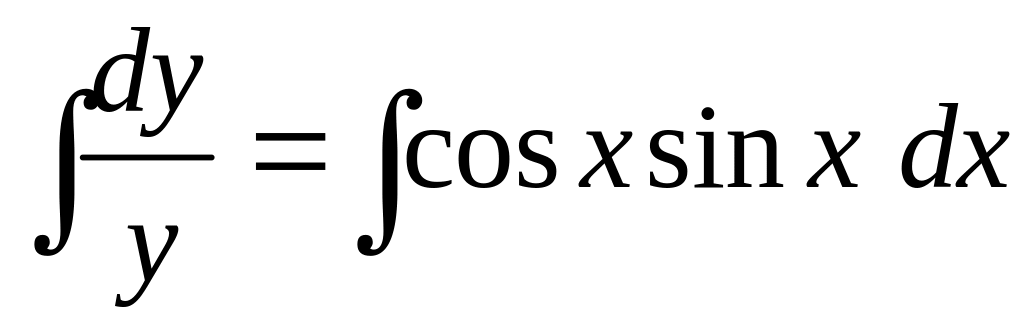 ,
,
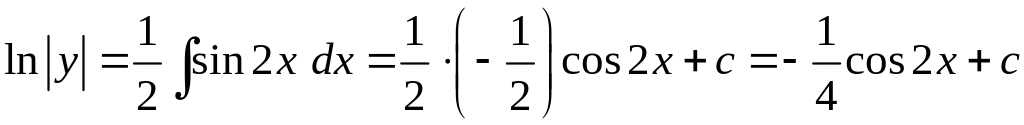 .
.
Следовательно,
выражение
 – общий интеграл данного дифференциального
уравнения.
– общий интеграл данного дифференциального
уравнения.
Пример 41. Найти общее решение дифференциальных уравнений первого порядка:
а)
![]() ;
б)
;
б)
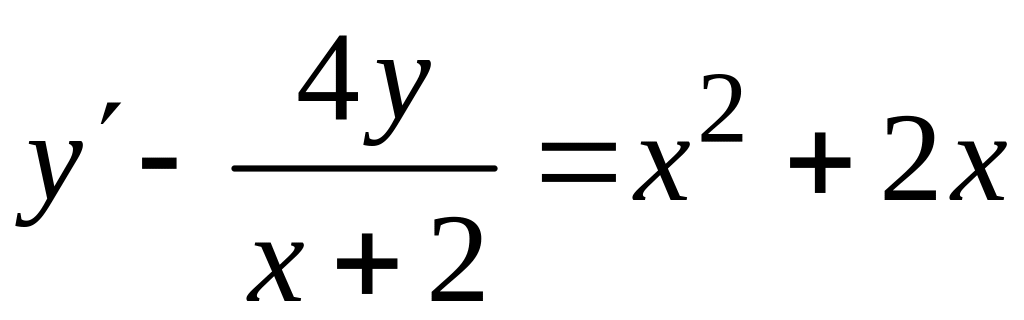 ;
в)
;
в)
![]() .
.
Решение. а) Разделим обе части данного уравнения на :
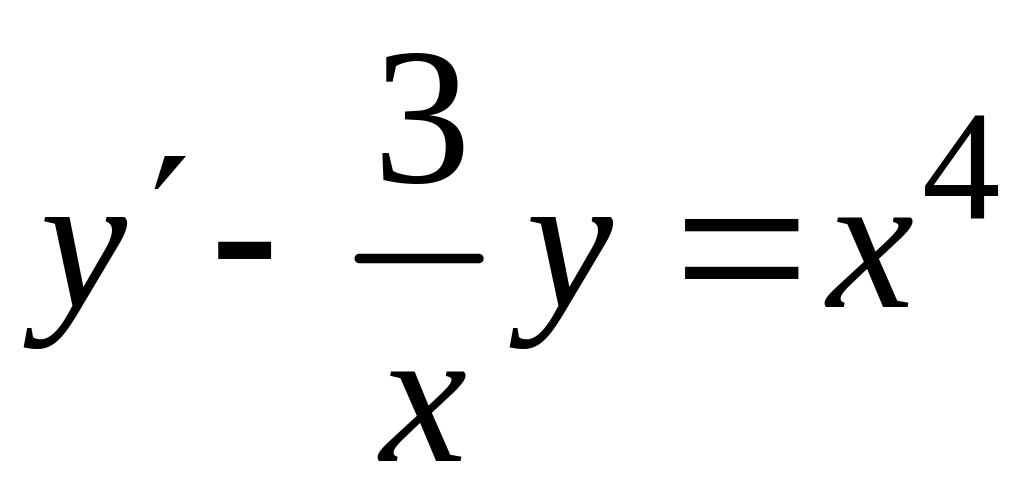 .
.
Данное уравнение является линейным дифференциальным уравнением первого порядка, т.к. оно имеет вид
![]() ,
,
где
 ,
,
![]() .
Будем искать решение в виде
.
Будем искать решение в виде
![]() ,
где
и
– некоторые функции, зависящие от
.
Тогда производная
,
где
и
– некоторые функции, зависящие от
.
Тогда производная
![]() и данное уравнение примет вид
и данное уравнение примет вид
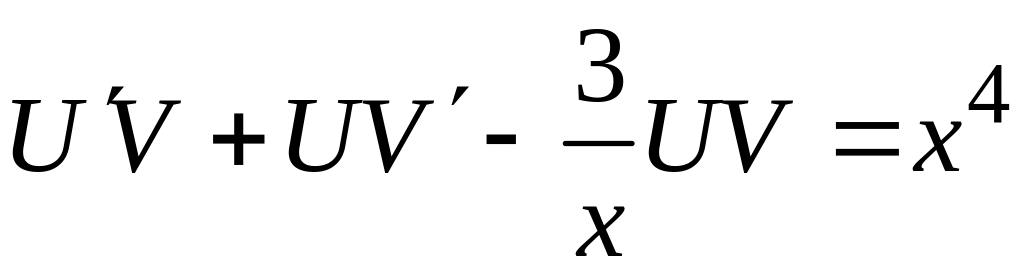 ,
,
или
 .
(7)
.
(7)
Т.к. искомая функция представлена в виде произведения двух неизвестных функций, то одну из них можно выбрать произвольно. Выберем функцию так, чтобы выражение, стоящее в круглых скобках равенства (7), обращалось в 0, т.е. чтобы выполнялось равенство
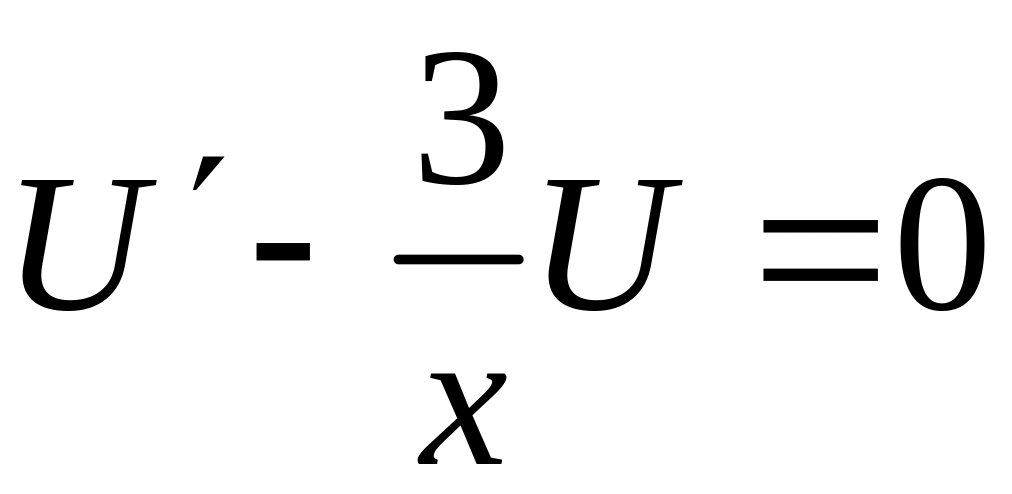 .
(8)
.
(8)
При выборе такой функции уравнение (7) примет вид
![]() .
(9)
.
(9)
Уравнение (8) является уравнением с разделяющимися переменными относительно и . Решим уравнение (8):
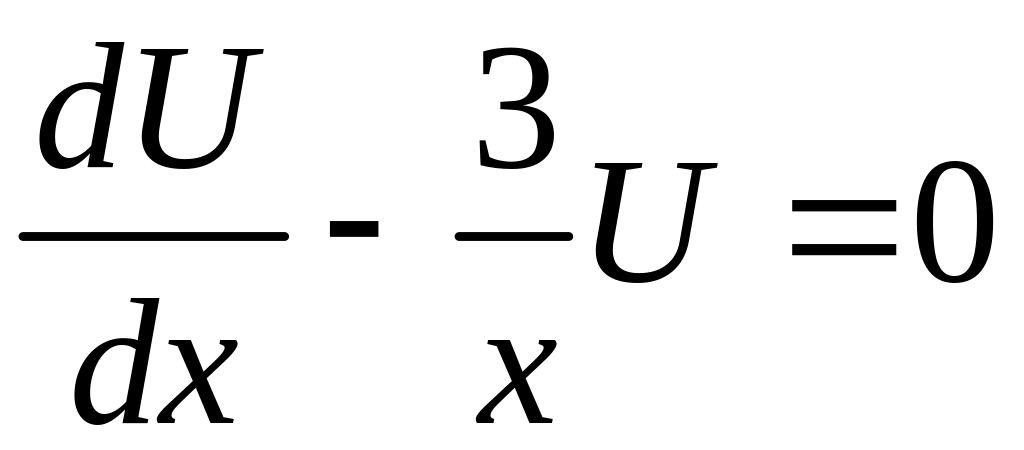 ;
;
 ;
;
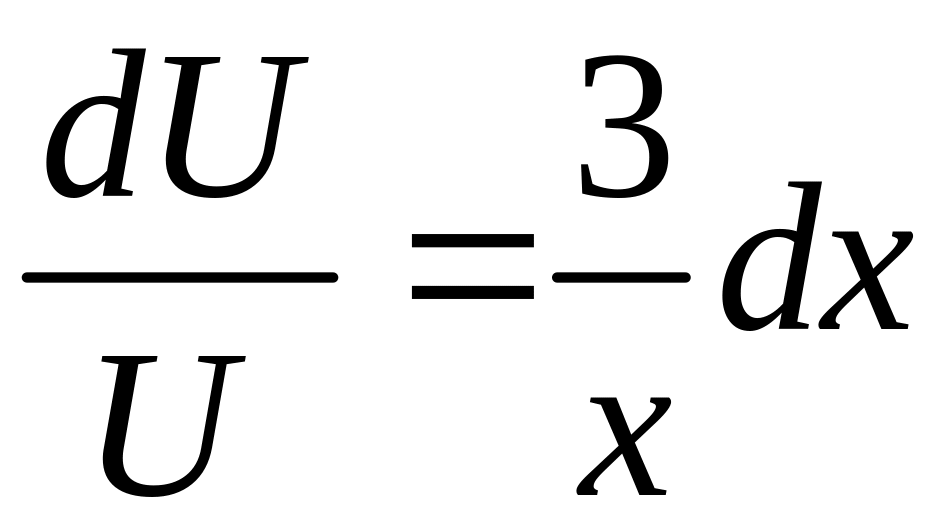 ;
;
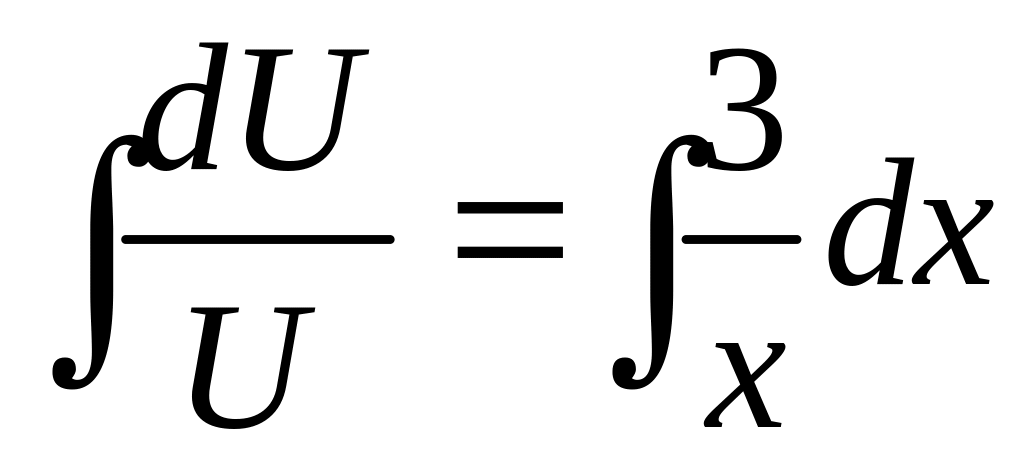 ;
;
![]() .
.
Чтобы
равенство (8) имело место, достаточно
найти хотя бы одно частное решение этого
уравнения. Поэтому для простоты при
интегрировании этого уравнения находим
частное решение, которое соответствует
значению произвольной постоянной
![]() :
:
![]() ;
;
![]() .
.
Найденное выражение для функции подставим в равенство (9). Получим:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
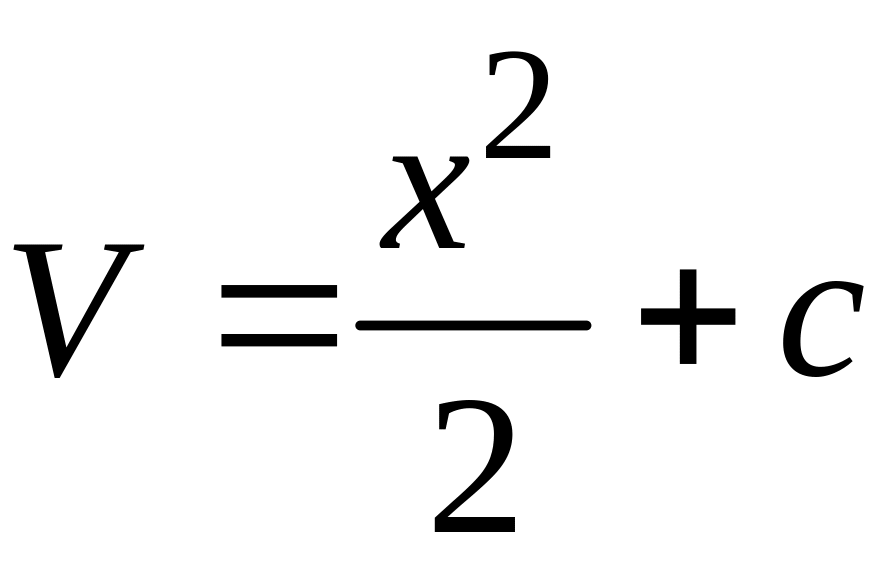 .
.
Тогда общее решение данного уравнения имеет вид
 .
.
б) Данное уравнение является линейным дифференциальным уравнением первого порядка, т.к. оно имеет вид
,
где
 ,
,
![]() .
Будем искать решение в виде
,
где
и
– некоторые функции, зависящие от
.
Тогда производная
и данное уравнение примет вид
.
Будем искать решение в виде
,
где
и
– некоторые функции, зависящие от
.
Тогда производная
и данное уравнение примет вид
 ,
,
или
 .
(10)
.
(10)
Т.к.
искомая функция
представлена в виде произведения двух
неизвестных функций, то одну из них
можно выбрать произвольно. Выберем
функцию
![]() так, чтобы выражение, стоящее в круглых
скобках равенства (10), обращалось в 0,
т.е. чтобы выполнялось равенство
так, чтобы выражение, стоящее в круглых
скобках равенства (10), обращалось в 0,
т.е. чтобы выполнялось равенство
 .
(11)
.
(11)
При выборе такой функции уравнение (10) примет вид
![]() .
(12)
.
(12)
Уравнение
(11) является уравнением с разделяющимися
переменными относительно
и
![]() .
Решим уравнение (11):
.
Решим уравнение (11):
 ;
;
 ;
;
 ;
;
 ,
,
![]() .
.
Чтобы
равенство (11) имело место, достаточно
найти хотя бы одно частное решение этого
уравнения. Поэтому для простоты при
интегрировании этого уравнения находим
частное решение, которое соответствует
значению произвольной постоянной
![]() :
:
![]() ;
;
![]() ;
;
![]() .
.
Найденное выражение для функции подставим в равенство (3). Получим:
![]() ;
;
 ;
;
 ;
;
 .
.
Вычислим отдельно

 .
.
Имеем
 .
.
Тогда общее решение данного уравнения запишется в виде

![]() .
.
в) Данное уравнение является уравнением Бернулли, т.к. оно имеет вид
![]() ,
,
![]() ,
,
где
![]() ,
,
![]() ,
,
![]() .
Будем искать решение в виде
.
Будем искать решение в виде
![]() ,
где
и
,
где
и
![]() — некоторые функции, зависящие от
.
Тогда производная
— некоторые функции, зависящие от
.
Тогда производная
![]() и данное уравнение примет вид
и данное уравнение примет вид
![]() ,
,
или
![]() .
(13)
.
(13)
Т.к. искомая функция представлена в виде произведения двух неизвестных функций, то одну из них можно выбрать произвольно. Выберем функцию так, чтобы выражение, стоящее в круглых скобках равенства (13), обращалось в 0, т.е. чтобы выполнялось равенство
![]() .
(14)
.
(14)
При выборе такой функции уравнение (13) примет вид
![]() .
(15)
.
(15)
Уравнение (14) является уравнением с разделяющимися переменными относительно и . Решим уравнение (14):
 ;
;
 ;
;
 ;
;
 ;
;
![]() .
.
Чтобы равенство (14) имело место, достаточно найти хотя бы одно частное решение этого уравнения. Поэтому для простоты при интегрировании этого уравнения находим частное решение, которое соответствует значению произвольной постоянной :
![]() ;
;
![]() .
.
Найденное выражение для функции подставим в равенство (15). Получим:
![]() ;
;
 ;
;
 ;
;
![]() ;
;
 ;
;
 (
(![]() );
);
 .
.
Тогда общее решение данного уравнения имеет вид
 .
.
Пример 42. Найти общее решение (общий интеграл) дифференциальных уравнений первого порядка:
а)
![]() ;
б)
;
б)
 .
.
Решение.
а) Выразим производную
![]() в данном равенстве. Получим:
в данном равенстве. Получим:
 .
(16)
.
(16)
Правая
часть уравнения (16)
 является однородной функцией нулевой
степени переменных
и
,
т.е. она удовлетворяет условию
является однородной функцией нулевой
степени переменных
и
,
т.е. она удовлетворяет условию
![]() при любом множителе
при любом множителе
![]() .
Покажем подробно выполнение условия
однородности:
.
Покажем подробно выполнение условия
однородности:
 .
.
Значит,
уравнение (16) является однородным
дифференциальным уравнением первого
порядка. Для решения этого уравнения
выполним подстановку
 ,
тогда
,
тогда
![]() и
и
![]() .
После подстановки уравнение (16) примет
вид
.
После подстановки уравнение (16) примет
вид
 .
(17)
.
(17)
Решаем уравнение (17):
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
![]() (
(![]() );
);
![]() ;
;
![]() .
.
В последнем равенстве выполним подстановку :
 .
.
Тогда, раскрыв скобки, найдем общий интеграл данного уравнения
![]() .
.
б) В данном уравнении
(18)
правая
часть
 является однородной функцией нулевой
степени переменных
и
,
т.е. она удовлетворяет условию
при любом множителе
.
Покажем подробно выполнение условия
однородности:
является однородной функцией нулевой
степени переменных
и
,
т.е. она удовлетворяет условию
при любом множителе
.
Покажем подробно выполнение условия
однородности:
 .
.
Значит,
уравнение (18) является однородным
дифференциальным уравнением первого
порядка. Для решения этого уравнения
выполним подстановку
,
тогда
![]() и
.
После подстановки уравнение (18) примет
вид
и
.
После подстановки уравнение (18) примет
вид
 .
(19)
.
(19)
Решим уравнение (19):
![]() ;
;
 ;
;
 ;
;
 ;
;
![]() .
.
В последнем равенстве выполним подстановку и получим

– общий интеграл данного уравнения.
Пример 43. Найти частное решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами, удовлетворяющее указанным условиям:
а)
![]() ,
,
![]() ,
,
![]() ;
;
б)
![]() ,
,
![]() ,
,
![]() ;
;
в)
![]() ,
,
![]() ,
,
![]() .
.
Решение. а) Данному дифференциальному уравнению соответствует характеристическое уравнение:
![]() .
.
Решим
характеристическое уравнение. Его
дискриминант
![]() .
Тогда корни характеристического
уравнения
.
Тогда корни характеристического
уравнения
 ;
;
 .
.
Корни характеристического уравнения действительные и различные. Значит, общее решение дифференциального уравнения имеет вид
![]() .
.
Подчиним общее решение заданным условиям, чтобы найти частное решение дифференциального уравнения. Находим производную общего решения
 .
.
Подчинив
выражения для
и
заданным условиям
,
,
получим систему с неизвестными постоянными
![]() и
и
![]() :
:

![]()


![]()
 .
.
Тогда
![]() и частное решение имеет вид
и частное решение имеет вид
 .
.
б) Данному дифференциальному уравнению соответствует характеристическое уравнение:
![]() .
.
Решим
характеристическое уравнение. Его
дискриминант
![]() .
Тогда корни характеристического
уравнения
.
Тогда корни характеристического
уравнения
 ;
;
 .
.
Корни
характеристического уравнения
действительные и совпадающие, т.е.
![]() .
Значит, общее решение дифференциального
уравнения имеет вид
.
Значит, общее решение дифференциального
уравнения имеет вид
![]() .
.
Подчиним общее решение заданным условиям, чтобы найти частное решение дифференциального уравнения. Находим производную общего решения
![]() .
.
Подчинив выражения для и заданным условиям , , получим систему с неизвестными постоянными и :



 .
.
Тогда
 и частное решение дифференциального
уравнения имеет вид
и частное решение дифференциального
уравнения имеет вид
 .
.
в) Данному дифференциальному уравнению соответствует характеристическое уравнение:
![]() .
.
Решим
характеристическое уравнение. Его
дискриминант
![]() .
Значит, действительных корней
характеристическое уравнение не имеет.
В этом случае общее решение дифференциального
уравнения имеет вид
.
Значит, действительных корней
характеристическое уравнение не имеет.
В этом случае общее решение дифференциального
уравнения имеет вид
![]() ,
,
где
 ,
,
 ,
,
![]() и
и
![]() – коэффициенты в характеристическом
уравнении при слагаемых
– коэффициенты в характеристическом
уравнении при слагаемых
![]() и
и
![]() соответственно. Для данного дифференциального
уравнения
соответственно. Для данного дифференциального
уравнения
![]() ,
,
![]() ,
,
 ,
,
 .
Тогда общее решение данного дифференциального
уравнения имеет вид
.
Тогда общее решение данного дифференциального
уравнения имеет вид
![]() .
.
Подчиним общее решение заданным условиям, чтобы найти частное решение дифференциального уравнения. Находим производную общего решения
![]() .
.
Подчинив выражения для и заданным условиям , , получим систему с неизвестными постоянными и :



Тогда частное решение имеет вид
 .
.
Пример 44. Найти общее решение неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами
![]() .
.
Решение. 1) Найдем сначала общее решение соответствующего однородного дифференциального уравнения
![]() .
.
Составим характеристическое уравнение
![]() .
.
Решив
его, находим корни характеристического
уравнения
![]() .
Т.к. корни действительные и совпадающие,
то общее решение однородного
дифференциального уравнения запишется
в виде
.
Т.к. корни действительные и совпадающие,
то общее решение однородного
дифференциального уравнения запишется
в виде
![]() .
.
2)
Найдем частное решение данного
неоднородного дифференциального
уравнения. Правая часть неоднородного
дифференциального уравнения
![]() представима в виде
представима в виде
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() – старшая степень многочлена
– старшая степень многочлена
![]() .
.
Число
является корнем характеристического
уравнения второй кратности, т.е. совпадает
и с
![]() ,
и с
,
и с
![]() .
Значит, при записи частного решения
нужно добавить множитель
.
Значит, при записи частного решения
нужно добавить множитель
![]() ,
степень которого совпадает с кратностью
коэффициента
.
Тогда частное решение будем искать в
виде
,
степень которого совпадает с кратностью
коэффициента
.
Тогда частное решение будем искать в
виде
![]() ,
где произвольный многочлен
,
где произвольный многочлен
![]() имеет ту же степень, что и
.
Таким образом, частное решение данного
неоднородного дифференциального
уравнения запишется так
имеет ту же степень, что и
.
Таким образом, частное решение данного
неоднородного дифференциального
уравнения запишется так
![]() .
.
Найдем производные первого и второго порядка от частного решения. Получим

 ,
,


 .
.
Подставим производные вместе с самим решением в заданное неоднородное дифференциальное уравнение. Получим

 .
.
Сократив
на
![]() ,
получим следующее равенство
,
получим следующее равенство
![]()
![]() .
.
После приведения подобных слагаемых имеем
![]() .
.
Из
последнего равенства следует
![]() ,
,
![]() .
Тогда частное решение неоднородного
дифференциального уравнения имеет вид
.
Тогда частное решение неоднородного
дифференциального уравнения имеет вид
 .
.
3)
Запишем общее решение данного неоднородного
дифференциального уравнения как сумму
общего решения однородного уравнения
![]() и частного решения неоднородного
и частного решения неоднородного
![]() :
:
 .
.
Пример 45. Найти общее решение неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами
![]() .
.
Решение. 1) Найдем сначала общее решение соответствующего однородного дифференциального уравнения
![]() .
.
Составим характеристическое уравнение
![]() .
.
Решив
его, находим корни характеристического
уравнения
![]() ,
,
![]() .
Т.к. корни действительные и различные,
то общее решение однородного
дифференциального уравнения запишется
в виде
.
Т.к. корни действительные и различные,
то общее решение однородного
дифференциального уравнения запишется
в виде
![]() .
.
2)
Найдем частное решение данного
неоднородного дифференциального
уравнения. Правая часть неоднородного
дифференциального уравнения
![]() представима в виде
,
где
представима в виде
,
где
![]() ,
,
![]() ,
,
![]() – старшая степень многочлена
.
– старшая степень многочлена
.
Число
является корнем характеристического
уравнения первой кратности, т.е. совпадает
с
.
Значит, при записи частного решения
нужно добавить множитель
![]() ,
степень которого совпадает с кратностью
коэффициента
.
Тогда частное решение будем искать в
виде
,
степень которого совпадает с кратностью
коэффициента
.
Тогда частное решение будем искать в
виде
![]() ,
где произвольный многочлен
имеет ту же степень, что и
.
Таким образом, частное решение данного
неоднородного дифференциального
уравнения запишется так
,
где произвольный многочлен
имеет ту же степень, что и
.
Таким образом, частное решение данного
неоднородного дифференциального
уравнения запишется так
![]() .
.
Найдем производные первого и второго порядка от частного решения. Получим
![]() ,
,
![]() .
.
Подставим производные в заданное неоднородное дифференциальное уравнение. Получим
![]()
или
![]() .
.
Приравняем коэффициенты при одинаковых степенях в левой и правой частях последнего равенства. Получим систему уравнений с тремя неизвестными:



Тогда частное решение неоднородного дифференциального уравнения имеет вид
 .
.
3) Запишем общее решение данного неоднородного дифференциального уравнения как сумму общего решения однородного уравнения и частного решения неоднородного :
 .
.
Пример 46. Найти общее решение неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами
![]() .
.
Решение. 1) Найдем сначала общее решение соответствующего однородного дифференциального уравнения
![]() .
.
Составим характеристическое уравнение
![]() .
.
Решив
его, находим корни характеристического
уравнения
,
![]() .
Т.к. корни действительные и различные,
то общее решение однородного
дифференциального уравнения запишется
в виде
.
Т.к. корни действительные и различные,
то общее решение однородного
дифференциального уравнения запишется
в виде
![]() .
.
2)
Найдем частное решение данного
неоднородного дифференциального
уравнения. Правая часть неоднородного
дифференциального уравнения
![]() представима в виде
,
где
представима в виде
,
где
![]() ,
,
![]() ,
,
![]() – старшая степень многочлена
.
– старшая степень многочлена
.
Число не является корнем характеристического уравнения. Значит, при записи частного решения не нужно добавлять множитель со степенью .
Тогда
частное решение будем искать в виде
![]() ,
где произвольный многочлен
имеет ту же степень, что и
.
Таким образом, частное решение данного
неоднородного дифференциального
уравнения запишется так
,
где произвольный многочлен
имеет ту же степень, что и
.
Таким образом, частное решение данного
неоднородного дифференциального
уравнения запишется так
![]() .
.
Найдем производные первого и второго порядка от частного решения. Получим
![]() ,
,
![]() .
.
Подставим производные в заданное неоднородное дифференциальное уравнение. Получим
![]()
или
![]() .
.
Из
последнего равенства находим, что
![]() .
Тогда частное решение неоднородного
дифференциального уравнения имеет вид
.
Тогда частное решение неоднородного
дифференциального уравнения имеет вид
 .
.
3) Запишем общее решение данного неоднородного дифференциального уравнения как сумму общего решения однородного уравнения и частного решения неоднородного :
 .
.
