
- •Кафедра высшей математики
- •Порядок выполнения контрольных работ
- •Рекомендуемая литература
- •Справочный материал
- •Указания к выполнению контрольной работы 1
- •Примеры решения задач
- •Контрольная работа 1
- •Указания к выполнению контрольной работы 2
- •Примеры решения задач
- •Контрольная работа 2
- •Указания к выполнению контрольной работы 3
- •Примеры решения задач
- •Контрольная работа 3
- •Указания к выполнению контрольной работы 4
- •Примеры решения задач
- •Контрольная работа 4
- •Содержание
- •Ответственный за выпуск м.Г. Плотников Корректор г.Н. Елисеева
Примеры решения задач
Пример
6. Вычислить
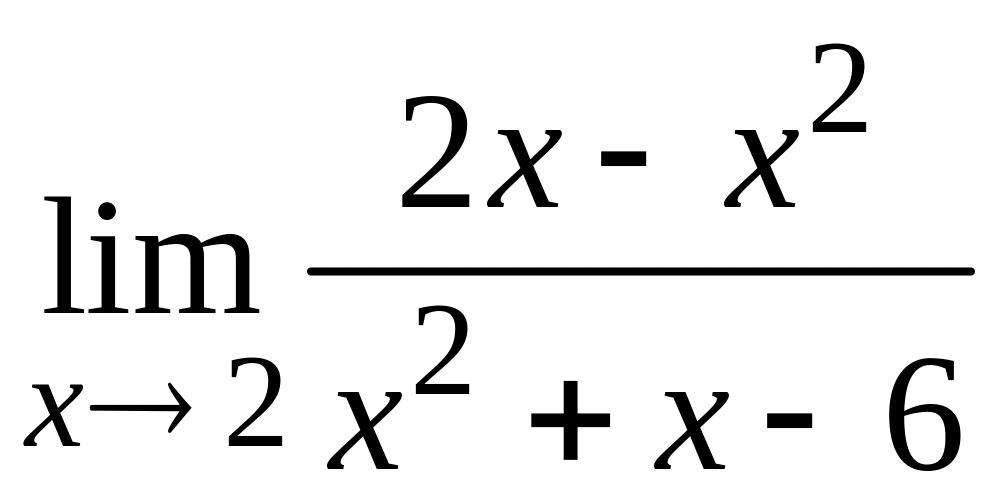 .
.
Решение.
Непосредственная подстановка предельного
значения аргумента
![]() в выражение, стоящее под знаком предела,
приводит к неопределенности вида
.
Для раскрытия этой неопределенности
разложим числитель и знаменатель на
множители и сократим члены дроби на
общий множитель
в выражение, стоящее под знаком предела,
приводит к неопределенности вида
.
Для раскрытия этой неопределенности
разложим числитель и знаменатель на
множители и сократим члены дроби на
общий множитель
![]() .
Множитель
.
Множитель
![]() при
при
![]() ,
т.к. переменная
только стремится к предельному значению
,
т.к. переменная
только стремится к предельному значению
![]() ,
но не совпадает с ним. При разложении
на множители числителя вынесем за скобку
общий множитель
,
при разложении знаменателя используем
формулу для квадратного трехчлена (см.
раздел Справочный
материал, Основные
алгебраические тождества).
Получим:
,
но не совпадает с ним. При разложении
на множители числителя вынесем за скобку
общий множитель
,
при разложении знаменателя используем
формулу для квадратного трехчлена (см.
раздел Справочный
материал, Основные
алгебраические тождества).
Получим:

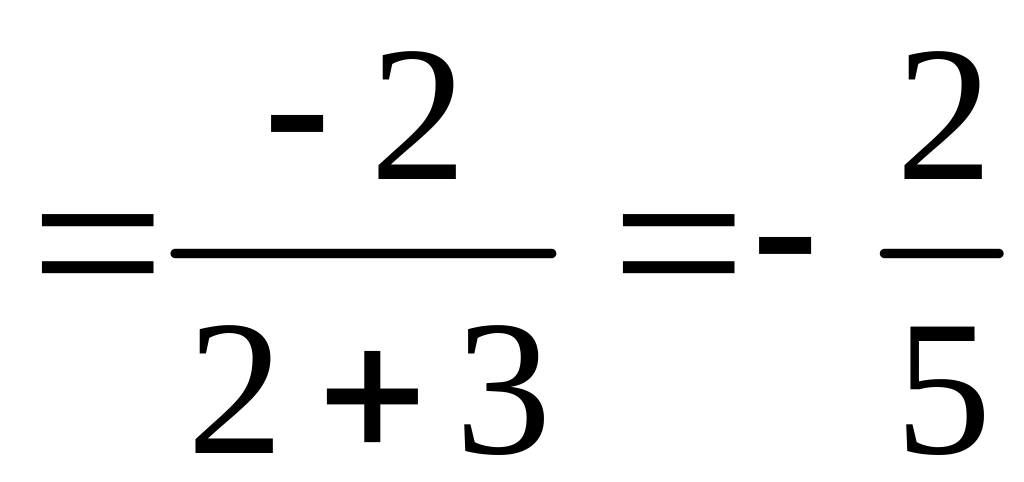 .
.
Пример
7. Вычислить
 .
.
Решение.
Непосредственная подстановка предельного
значения аргумента
![]() в выражение, стоящее под знаком предела,
приводит к неопределенности вида
.
Для раскрытия этой неопределенности
разложим числитель и знаменатель на
множители и сократим члены дроби на
общий множитель
в выражение, стоящее под знаком предела,
приводит к неопределенности вида
.
Для раскрытия этой неопределенности
разложим числитель и знаменатель на
множители и сократим члены дроби на
общий множитель
![]() .
Множитель
.
Множитель
![]() при
при
![]() ,
т.к. переменная
только стремится к предельному значению
,
т.к. переменная
только стремится к предельному значению
![]() ,
но не совпадает с ним. При разложении
на множители числителя используем
формулу для разности квадратов,
знаменателя – формулу для разложения
квадратного трехчлена (см. раздел
Справочный
материал, Основные
алгебраические тождества).
,
но не совпадает с ним. При разложении
на множители числителя используем
формулу для разности квадратов,
знаменателя – формулу для разложения
квадратного трехчлена (см. раздел
Справочный
материал, Основные
алгебраические тождества).
Получим:

 .
.
Пример
8. Вычислить
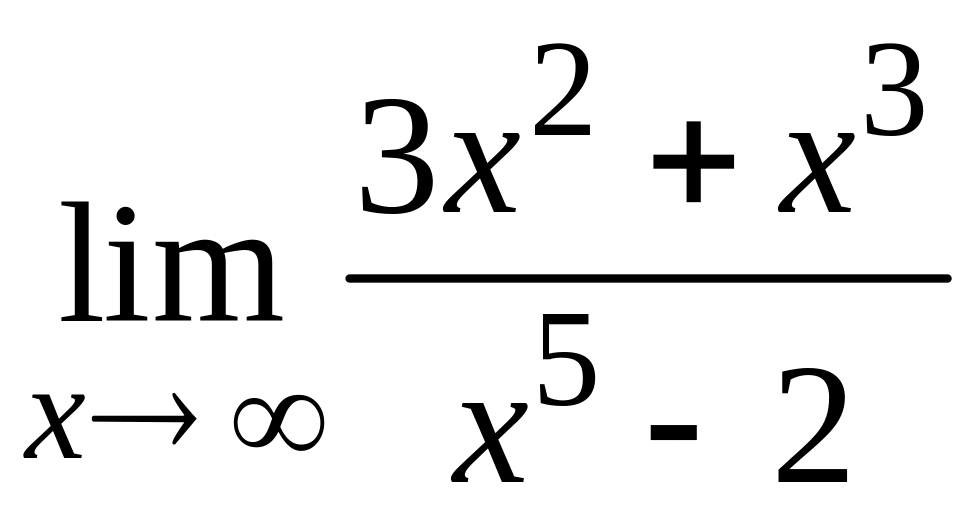 .
.
Решение.
При
![]() и числитель, и знаменатель дроби, стоящей
под знаком предела, стремятся к
и числитель, и знаменатель дроби, стоящей
под знаком предела, стремятся к
![]() .
Т.е. имеем неопределенность вида
.
Для раскрытия этой неопределенности
вынесем в числителе и знаменателе за
скобку наибольшую степень аргумента
(в данном примере это
.
Т.е. имеем неопределенность вида
.
Для раскрытия этой неопределенности
вынесем в числителе и знаменателе за
скобку наибольшую степень аргумента
(в данном примере это
![]() )
и сократим члены дроби на общий множитель.
Получим:
)
и сократим члены дроби на общий множитель.
Получим:
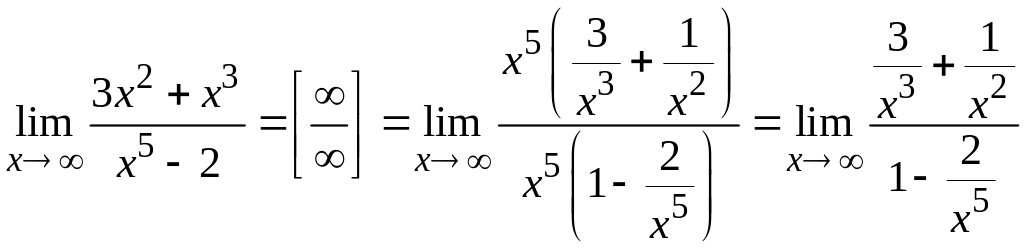 .
.
Так
как
,
то обратные величины степеней аргумента
,
а именно,
![]() ,
,
![]() ,
,
![]() стремятся к
стремятся к
![]() (см. раздел Справочный
материал, Таблица
пределов. Замечательные пределы и
следствия).
Находим:
(см. раздел Справочный
материал, Таблица
пределов. Замечательные пределы и
следствия).
Находим:
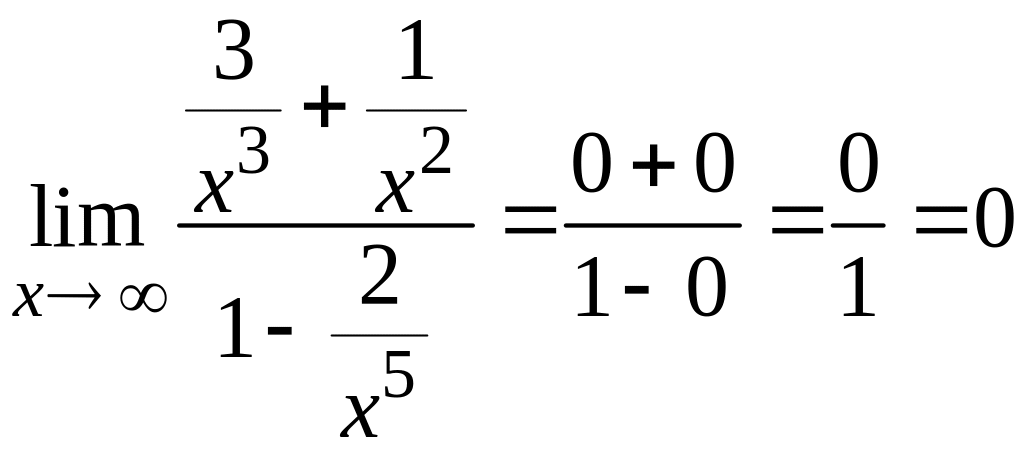 .
.
Пример
9. Вычислить
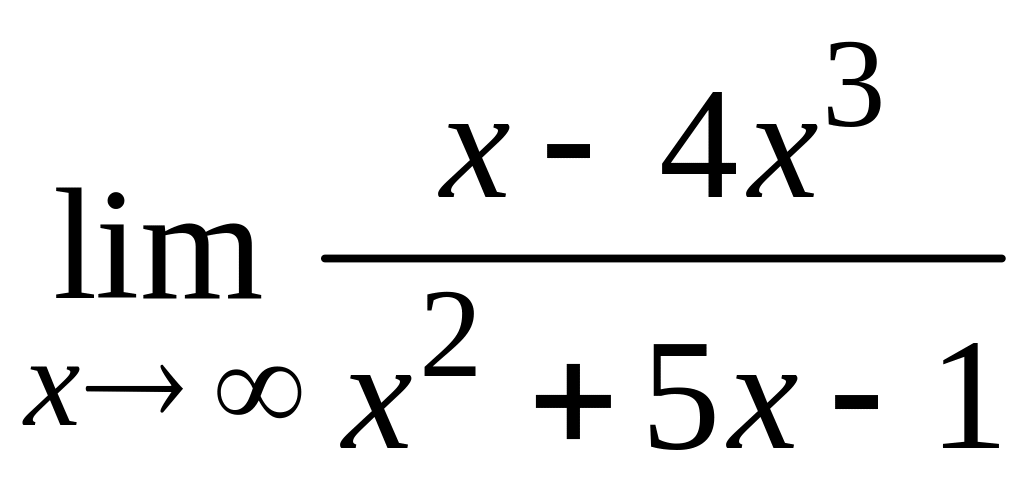 .
.
Решение.
При
и числитель, и знаменатель дроби, стоящей
под знаком предела, стремятся к
.
Т.е. имеем неопределенность вида
.
Для раскрытия этой неопределенности
вынесем в числителе и знаменателе за
скобку наибольшую степень аргумента
(в данном примере это
![]() )
и сократим члены дроби на общий множитель.
Получим:
)
и сократим члены дроби на общий множитель.
Получим:
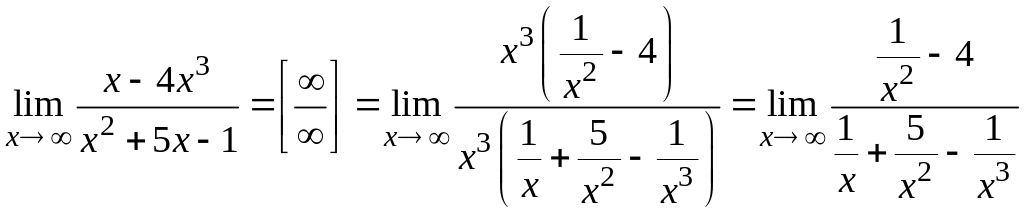 .
.
Т.к.
,
то обратные величины степеней аргумента
,
а именно,
![]() ,
,
,
,
![]() ,
,
![]() стремятся к
(см. раздел Справочный
материал, Таблица
пределов. Замечательные пределы и
следствия).
Находим:
стремятся к
(см. раздел Справочный
материал, Таблица
пределов. Замечательные пределы и
следствия).
Находим:
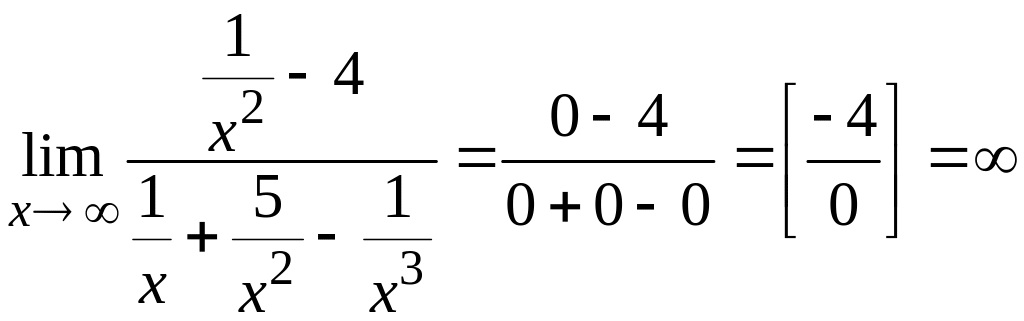 .
.
При вычислении окончательного результата использовалось то, что величина, обратная стремящейся к нулю, стремится к (см. раздел Справочный материал, Таблица пределов. Замечательные пределы и следствия).
Пример
10. Вычислить
 .
.
Решение.
Непосредственная подстановка предельного
значения аргумента
![]() в выражение, стоящее под знаком предела,
приводит к неопределенности вида
.
Для раскрытия этой неопределенности
используем первый замечательный предел
и следствия из него (см.
раздел Справочный
материал, Таблица
пределов. Замечательные пределы и
следствия).
И числитель, и знаменатель дроби умножим
и поделим одновременно на аргументы,
стоящие под знаком тригонометрических
функций синуса и тангенса. Тем самым мы
создадим выражения, участвующие в первом
замечательном пределе и его следствиях.
Получим:
в выражение, стоящее под знаком предела,
приводит к неопределенности вида
.
Для раскрытия этой неопределенности
используем первый замечательный предел
и следствия из него (см.
раздел Справочный
материал, Таблица
пределов. Замечательные пределы и
следствия).
И числитель, и знаменатель дроби умножим
и поделим одновременно на аргументы,
стоящие под знаком тригонометрических
функций синуса и тангенса. Тем самым мы
создадим выражения, участвующие в первом
замечательном пределе и его следствиях.
Получим:
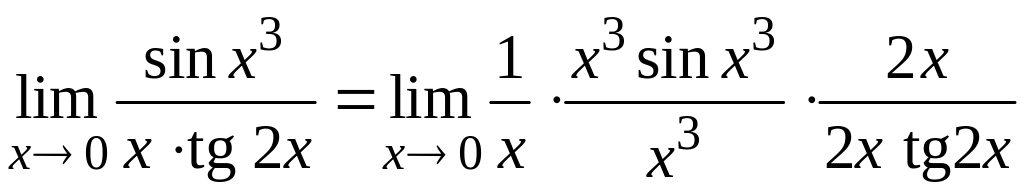 .
.
Т.к.
 и
и
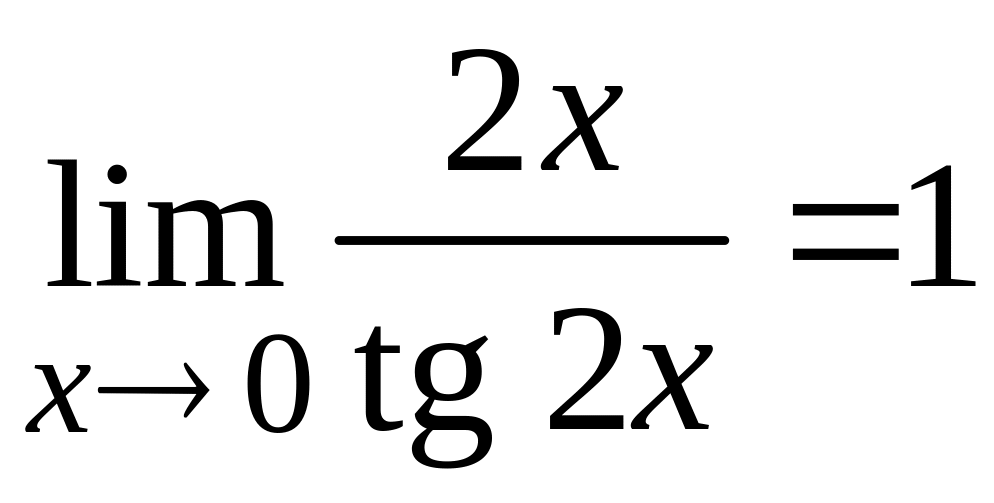 по первому замечательному пределу и
следствию из него, то получим:
по первому замечательному пределу и
следствию из него, то получим:
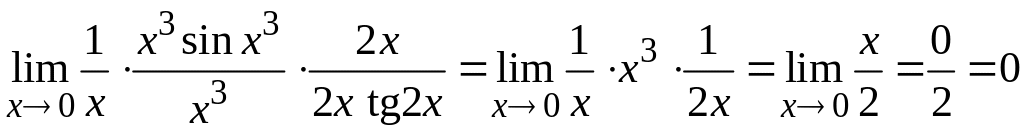 .
.
Пример
11. Вычислить
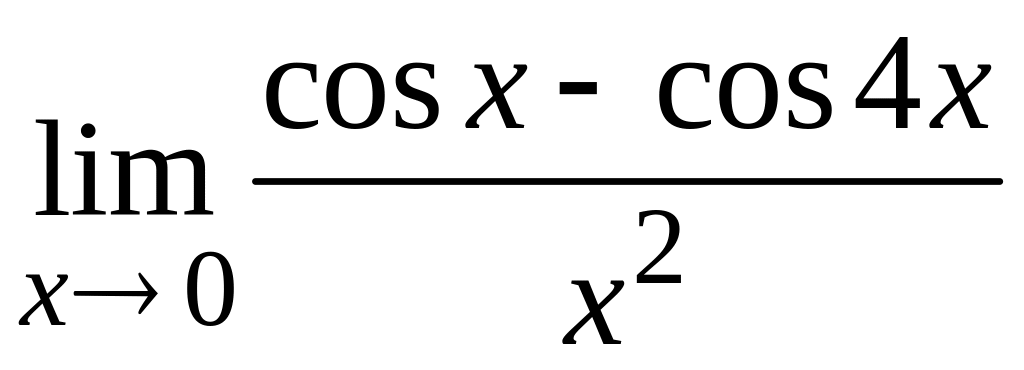 .
.
Решение. Непосредственная подстановка предельного значения аргумента в выражение, стоящее под знаком предела, приводит к неопределенности вида . Для раскрытия этой неопределенности используем первый замечательный предел и следствия из него (см. раздел Справочный материал, Таблица пределов. Замечательные пределы и следствия).
Преобразуем числитель, используя формулу для разности косинусов (см. раздел Справочный материал, Основные тригонометрические формулы). Будем иметь:
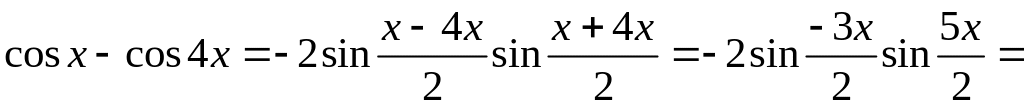
 .
.
Тогда
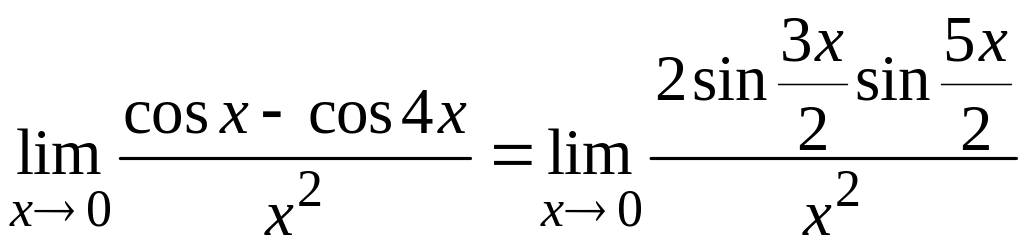 .
.
И числитель, и знаменатель дроби умножим и поделим одновременно на аргументы, стоящие под знаком тригонометрической функции синус. Тем самым мы создадим выражения, участвующие в первом замечательном пределе. Получим:
 .
.
Т.к.
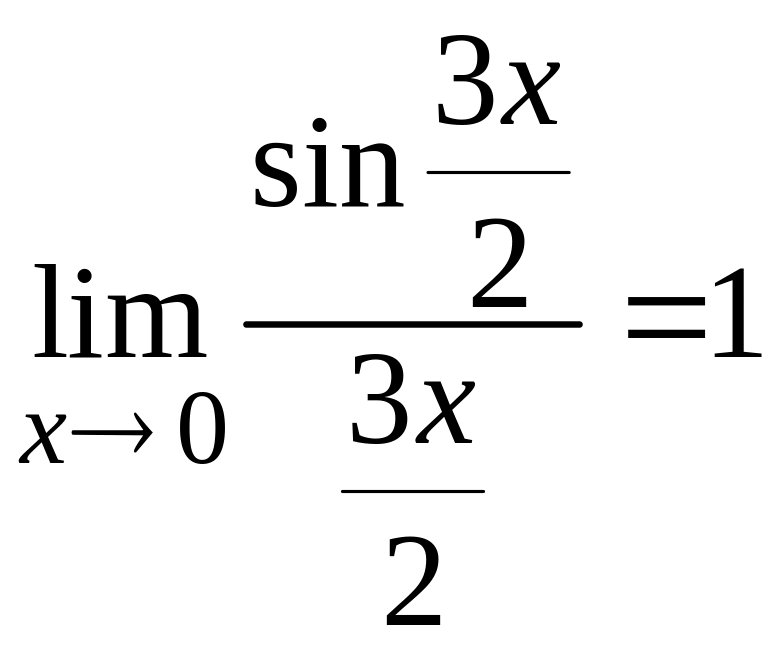 и
и
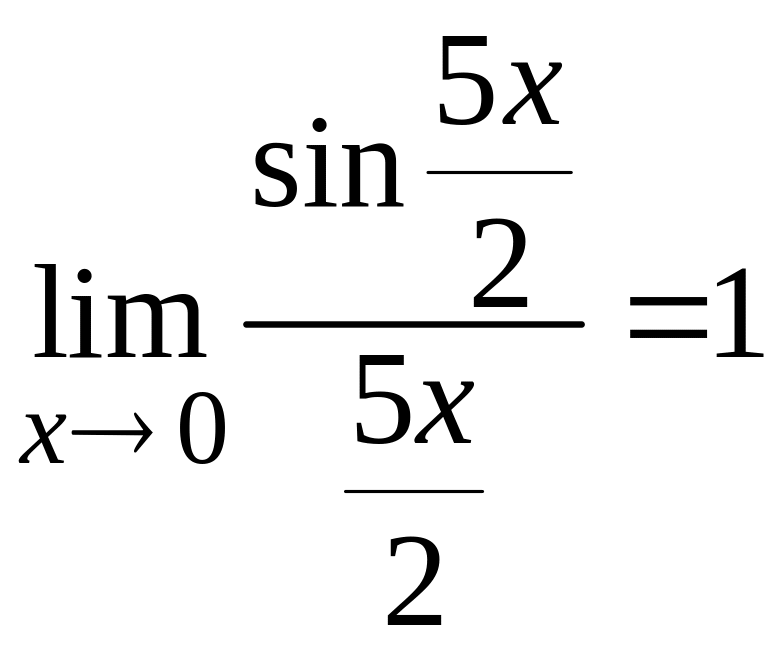 по первому замечательному пределу, то
получим:
по первому замечательному пределу, то
получим:
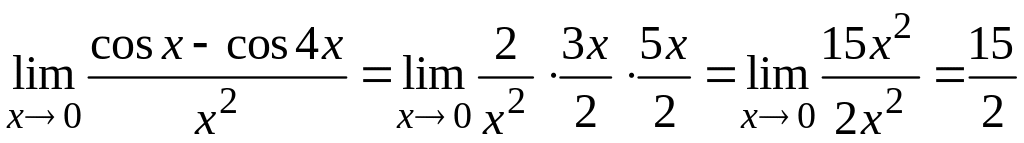 .
.
Пример
12. Вычислить
 .
.
Решение. Непосредственная подстановка предельного значения аргумента в выражение, стоящее под знаком предела, приводит к неопределенности вида . Для раскрытия этой неопределенности используем первый замечательный предел и следствия из него (см. раздел Справочный материал, Таблица пределов. Замечательные пределы и следствия). Преобразуем числитель, используя формулу понижения степени для функции синус (см. раздел Справочный материал, Основные тригонометрические формулы). Будем иметь:
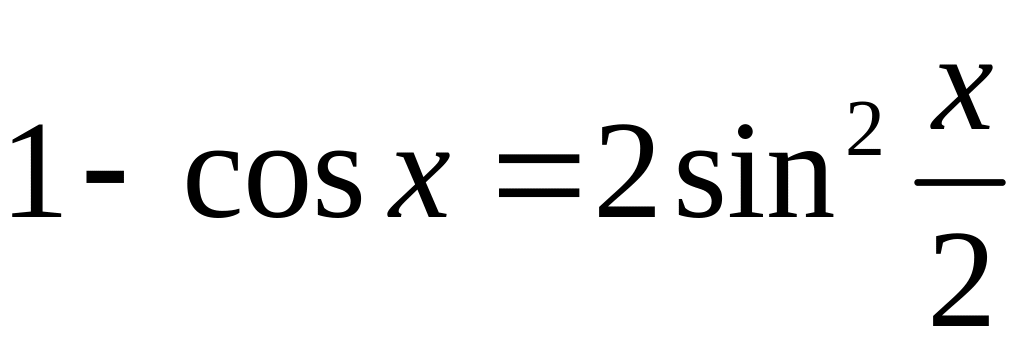 .
.
Тогда
 .
.
И числитель, и знаменатель дроби умножим и поделим одновременно на аргумент, стоящий под знаком тригонометрической функции синус. Тем самым мы создадим выражения, участвующие в следствии первого замечательного предела. Получим:
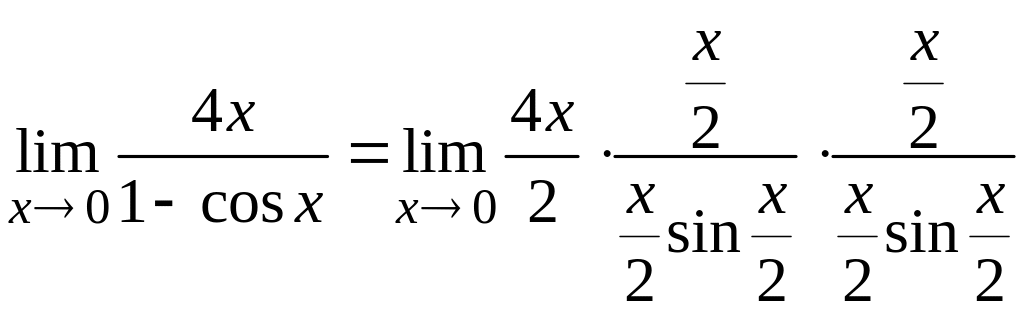 .
.
Т.к.
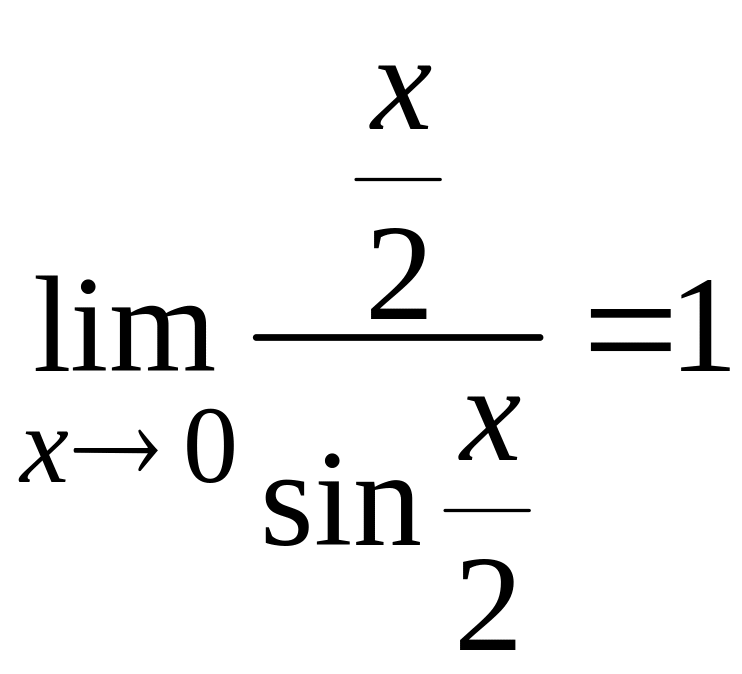 по следствию первого замечательного
предела, то получим:
по следствию первого замечательного
предела, то получим:
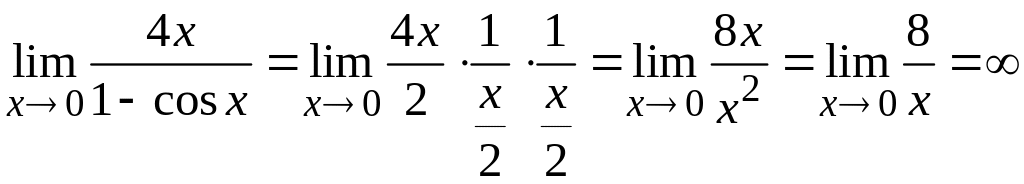 .
.
При вычислении окончательного результата использовалось то, что величина, обратная к стремящейся к , стремится к (см. раздел Справочный материал, Таблица пределов. Замечательные пределы и следствия).
Пример
13. Вычислить
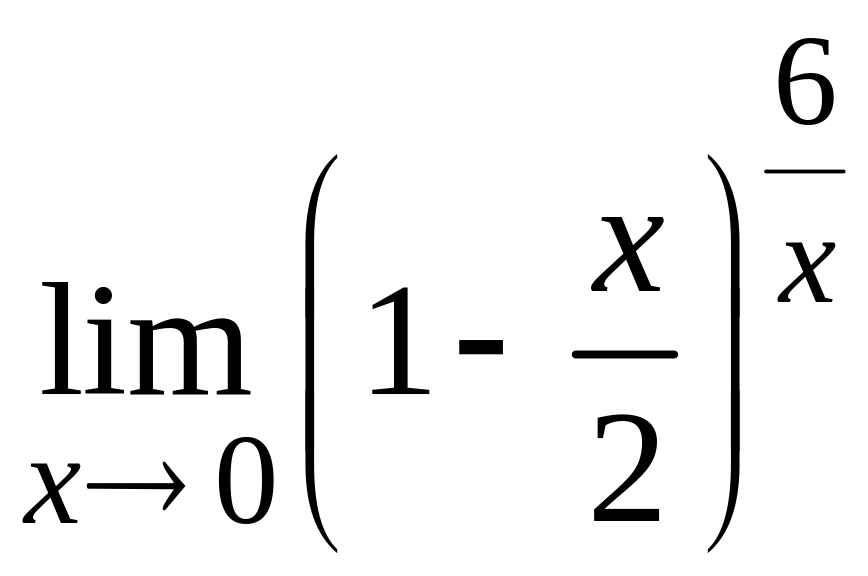 .
.
Решение. Вычислим отдельно пределы основания и показателя степени, стоящей под знаком предела. Найдем:
 ,
,
 ,
,
т.е.
имеем неопределенность вида
![]() .
Для раскрытия этой неопределенности
используем второй замечательный предел
(см.
раздел Справочный
материал, Таблица
пределов. Замечательные пределы и
следствия).
Для создания второго замечательного
предела проведем тождественные
преобразования выражения, стоящего
под знаком предела:
.
Для раскрытия этой неопределенности
используем второй замечательный предел
(см.
раздел Справочный
материал, Таблица
пределов. Замечательные пределы и
следствия).
Для создания второго замечательного
предела проведем тождественные
преобразования выражения, стоящего
под знаком предела:
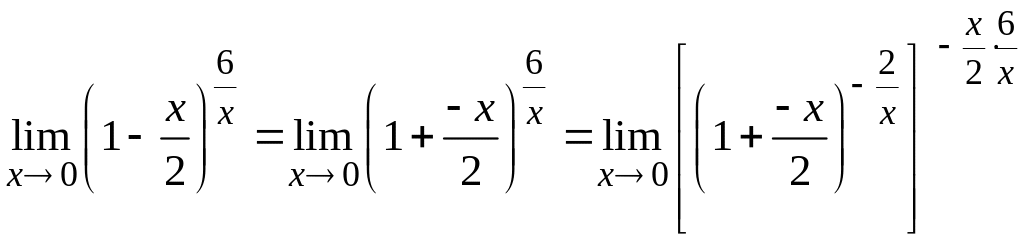 .
.
По второму замечательному пределу
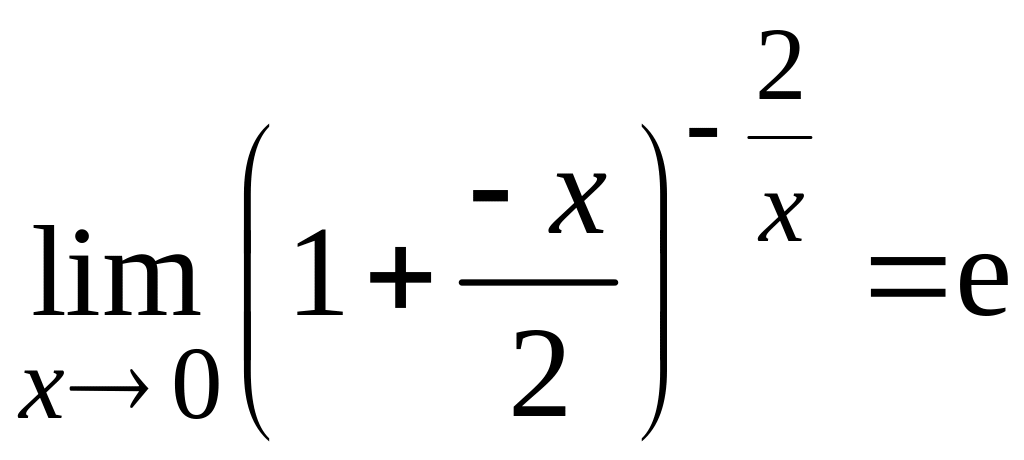 .
.
Предел показателя
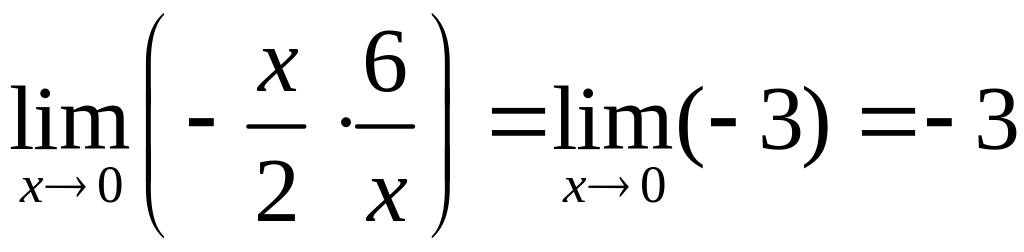 .
.
Тогда
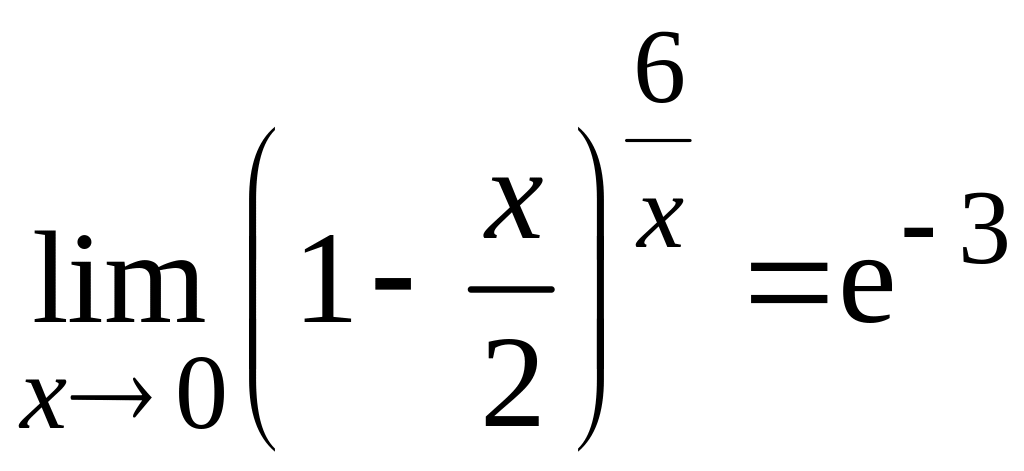 .
.
Пример
14. Вычислить
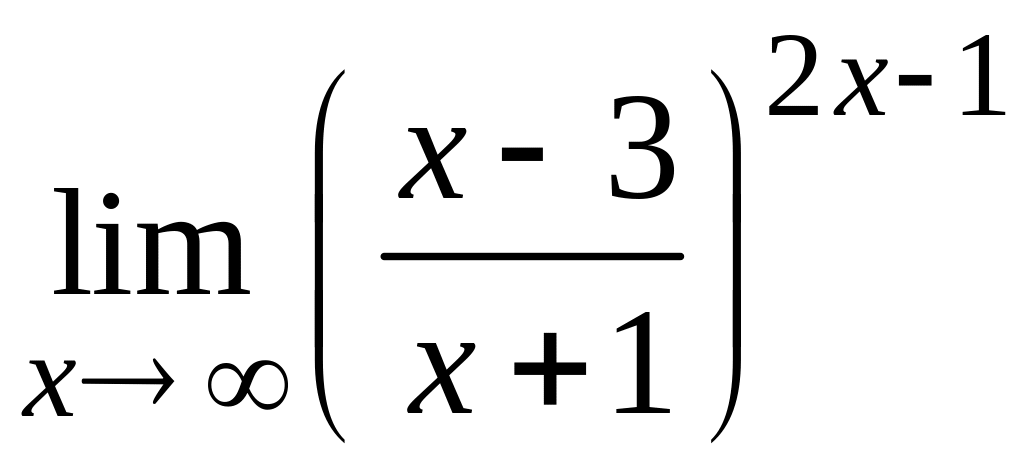 .
.
Решение. Вычислим отдельно пределы основания и показателя степени, стоящей под знаком предела. Найдем:
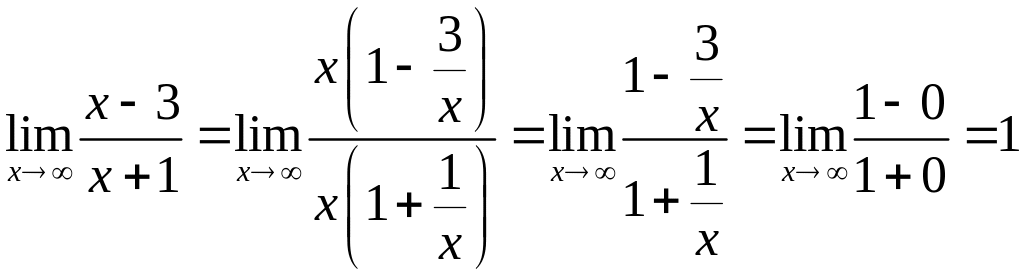 ,
,
![]() ,
,
т.е. имеем неопределенность вида . Для раскрытия этой неопределенности используем второй замечательный предел (см. раздел Справочный материал, Таблица пределов. Замечательные пределы и следствия). Для создания второго замечательного предела проведем тождественные преобразования выражения, стоящего под знаком предела:

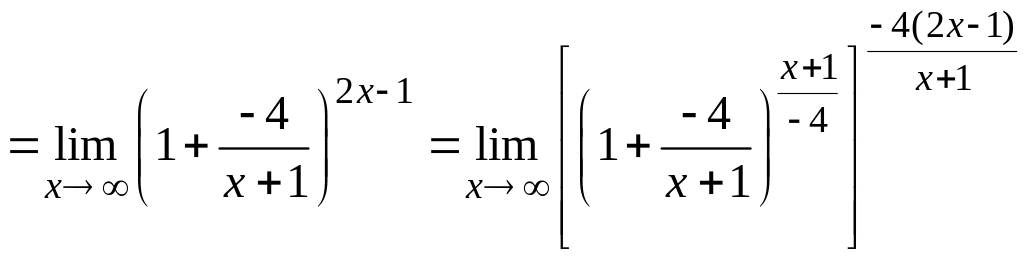 .
.
По второму замечательному пределу
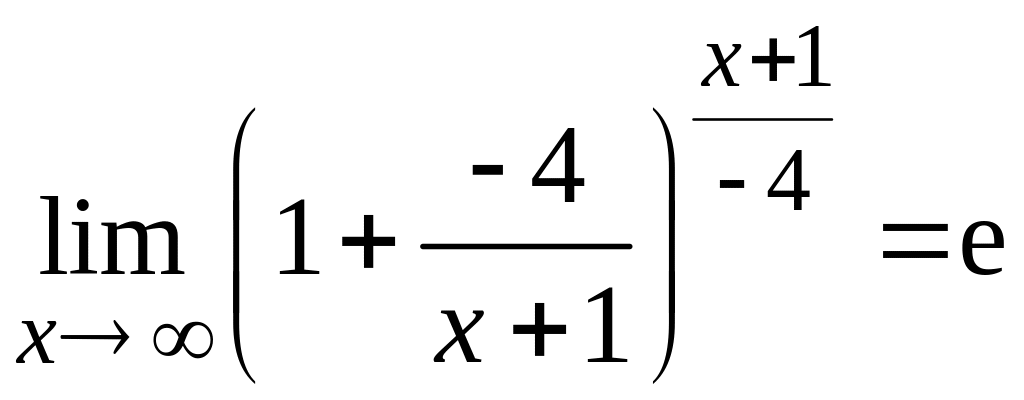 .
.
Предел показателя
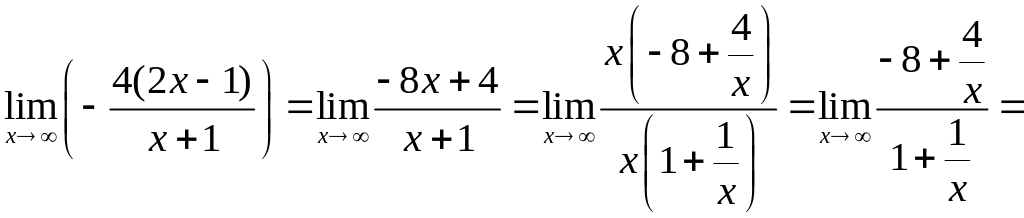
 .
.
Тогда
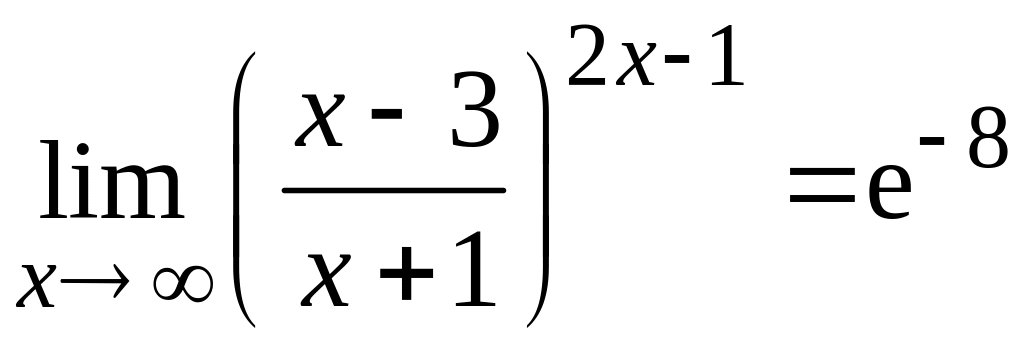 .
.
Пример 15. Функция задана кусочным образом, т.е. различными аналитическими выражениями для различных промежутков переменной . Требуется построить график функции и указать ее точки разрыва, если они имеются.

Решение.
Данная функция определена и непрерывна
в интервалах
![]() ,
,
![]() и
и
![]() .
При значениях переменной
.
При значениях переменной
![]() и
меняется аналитическое выражение
функции, следовательно, только в этих
точках функция может иметь разрыв.
Определим односторонние пределы функции
в точке
:
и
меняется аналитическое выражение
функции, следовательно, только в этих
точках функция может иметь разрыв.
Определим односторонние пределы функции
в точке
:
![]() ;
;
![]() .
.
Односторонние
пределы не совпадают, значит,
является точкой разрыва функции.
Определим односторонние пределы функции
в точке
![]() :
:
![]() ;
;
![]() .
.
Односторонние пределы совпадают между собой и совпадают со значением функции в точке , значит, функция непрерывна в этой точке (т.е. не является точкой разрыва).
П остроим
график данной функции.
остроим
график данной функции.
На
интервале
график функции совпадает с прямой
![]() ,
на отрезке
,
на отрезке
![]() график функции совпадает с параболой
график функции совпадает с параболой
![]() ,
на интервале
– с прямой
,
на интервале
– с прямой
![]() (см. рис. 10).
(см. рис. 10).
Р и с. 10
Пример 16. Функция задана кусочным образом, т.е. различными аналитическими выражениями для различных промежутков переменной . Требуется построить график функции и указать ее точки разрыва, если они имеются.
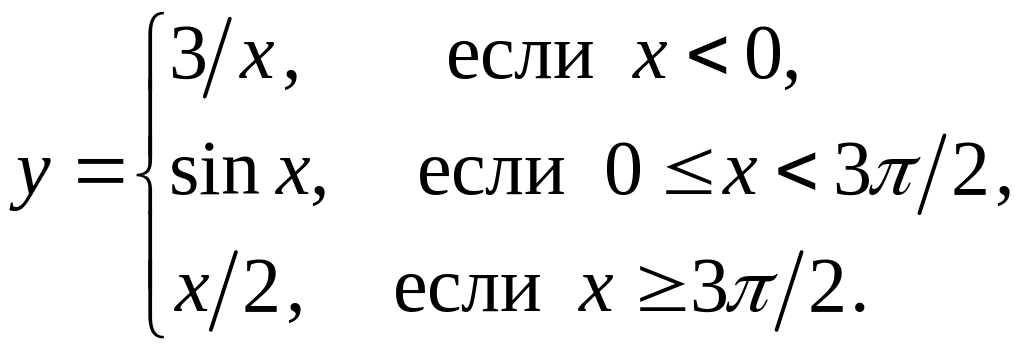
Решение.
Данная функция определена и непрерывна
в интервалах
![]() ,
,
![]() и
и
![]() .
При значениях переменной
и
.
При значениях переменной
и
![]() меняется аналитическое выражение
функции, следовательно, только в этих
точках функция может иметь разрыв.
Определим односторонние пределы функции
в точке
:
меняется аналитическое выражение
функции, следовательно, только в этих
точках функция может иметь разрыв.
Определим односторонние пределы функции
в точке
:
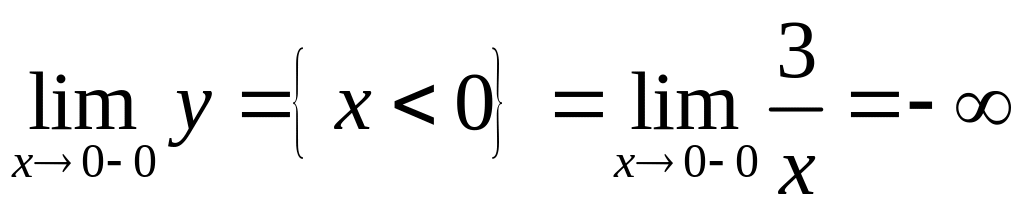 ;
;
![]() .
.
Односторонние пределы не совпадают, значит, является точкой разрыва функции. Определим односторонние пределы функции в точке :
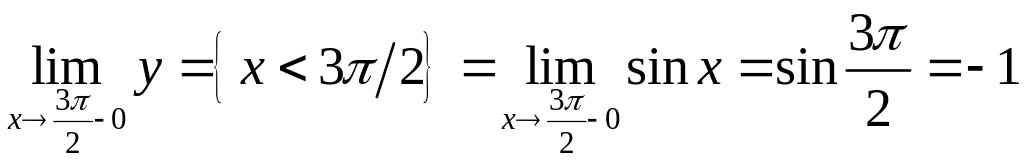 ;
;
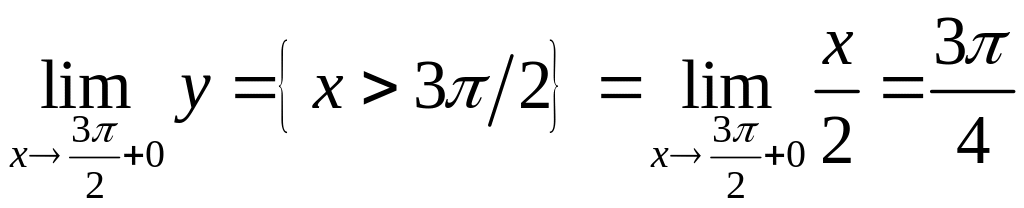 .
.
Односторонние
пределы не совпадают, значит, точка
является точкой разрыва функции. Построим
график данной функции. На интервале
график функции совпадает с гиперболой
![]() ,
на промежутке
,
на промежутке
![]() график функции совпадает с синусоидой
график функции совпадает с синусоидой
![]() ,
на промежутке
,
на промежутке
![]() – с прямой
– с прямой
![]() (см. рис. 11).
(см. рис. 11).

Р и с. 11
Пример
17. Найти
производные первого порядка
![]() данных функций.
данных функций.
а)
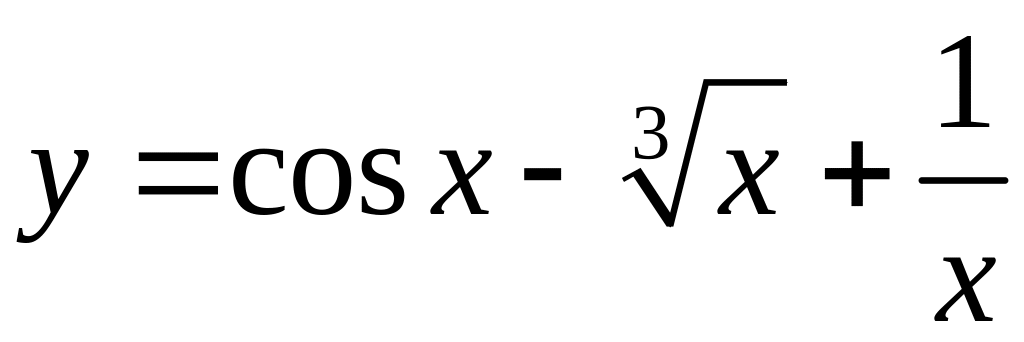 ;
г)
;
г)
![]() ;
;
б)
![]() ;
д)
;
д)
![]() ;
;
в)
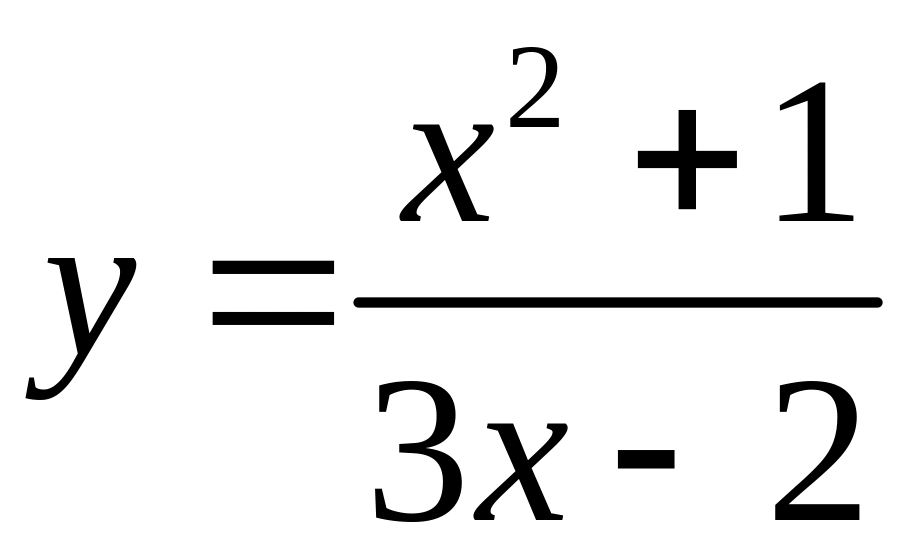 ;
е)
;
е)
![]() .
.
Решение.
а)
Требуется найти
 .
Под знаком производной стоит алгебраическая
сумма трех слагаемых. Производная
алгебраической суммы дифференцируемых
слагаемых равна той же сумме производных
каждого из слагаемых. Пользуясь табличными
формулами 2, 6, 7, 9 (см. раздел
Справочный
материал, Правила
дифференцирования. Таблица производных),
находим:
.
Под знаком производной стоит алгебраическая
сумма трех слагаемых. Производная
алгебраической суммы дифференцируемых
слагаемых равна той же сумме производных
каждого из слагаемых. Пользуясь табличными
формулами 2, 6, 7, 9 (см. раздел
Справочный
материал, Правила
дифференцирования. Таблица производных),
находим:
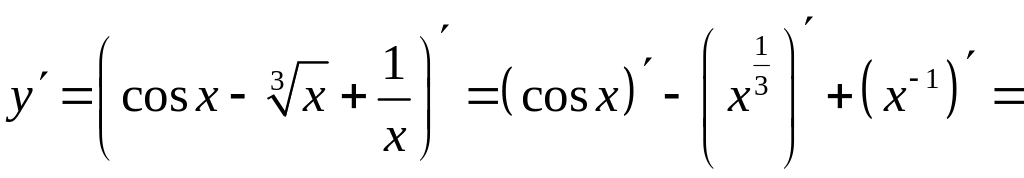
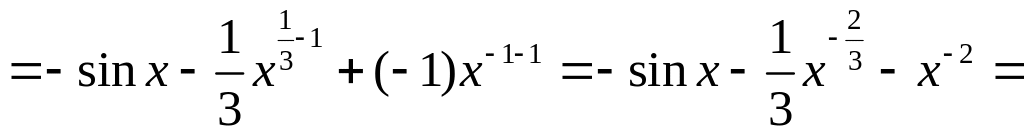
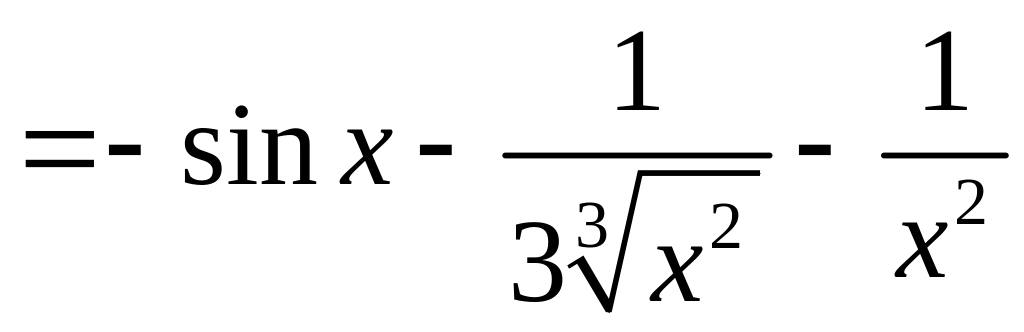 .
.
б)
Требуется найти
![]() .
Под знаком производной стоит произведение
двух множителей. Используем табличную
формулу 3 для производной произведения
дифференцируемых множителей (см. раздел
Справочный
материал, Правила
дифференцирования. Таблица производных).
Получим:
.
Под знаком производной стоит произведение
двух множителей. Используем табличную
формулу 3 для производной произведения
дифференцируемых множителей (см. раздел
Справочный
материал, Правила
дифференцирования. Таблица производных).
Получим:
![]() .
.
Для нахождения производных показательной функции и функции котангенс используем табличные формулы 6, 11 и 12 (см. раздел Справочный материал, Правила дифференцирования. Таблица производных). Найдем:

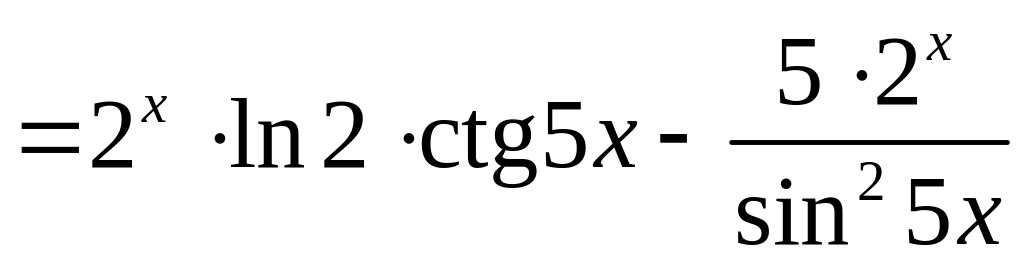 .
.
в)
Требуется найти
 .
Под знаком производной стоит частное
функций. Пользуясь табличной формулой
4 для нахождения производной частного
и формулами 5, 6, 7 для производной
постоянной и степенной функций (см.
раздел Справочный
материал, Правила
дифференцирования. Таблица производных),
находим:
.
Под знаком производной стоит частное
функций. Пользуясь табличной формулой
4 для нахождения производной частного
и формулами 5, 6, 7 для производной
постоянной и степенной функций (см.
раздел Справочный
материал, Правила
дифференцирования. Таблица производных),
находим:
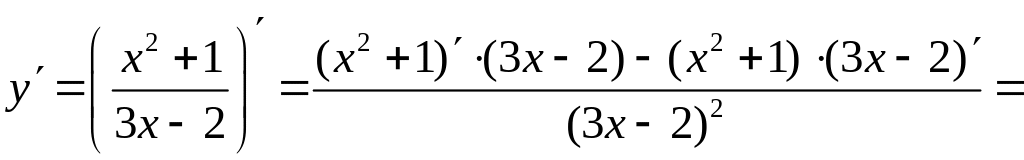
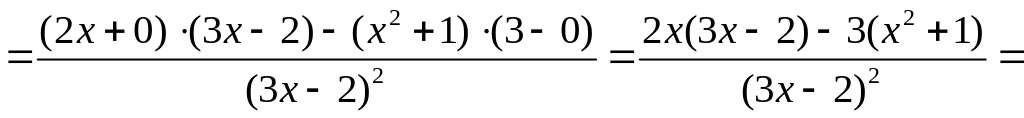
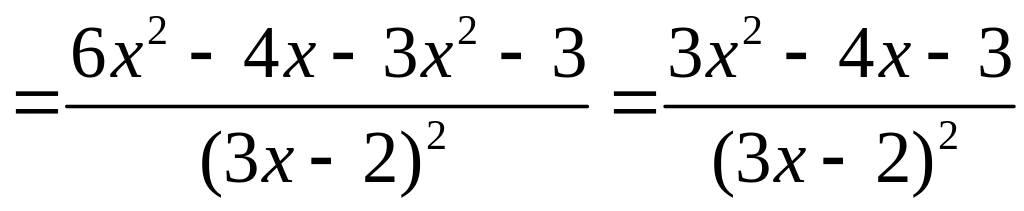 .
.
г)
Требуется найти
![]() .
Под знаком производной стоит сложная
функция вида
.
Под знаком производной стоит сложная
функция вида
![]() ,
где
,
где
![]() – внутренняя функция. Используем
табличную формулу 13 для нахождения
производной логарифмической функции
(см. раздел
Справочный
материал, Правила
дифференцирования. Таблица производных),
получим:
– внутренняя функция. Используем
табличную формулу 13 для нахождения
производной логарифмической функции
(см. раздел
Справочный
материал, Правила
дифференцирования. Таблица производных),
получим:
 .
.
Для нахождения производной внутренней функции используем табличные формулы 1, 6, 8 (см. раздел Справочный материал, Правила дифференцирования. Таблица производных), получим:
![]() .
.
Тогда
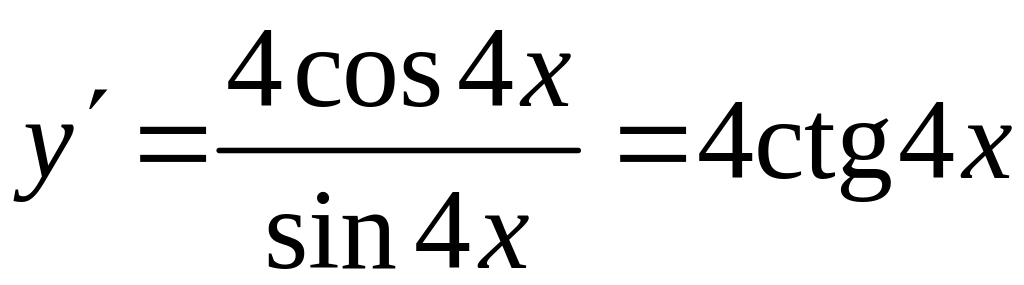 .
.
д)
Требуется найти
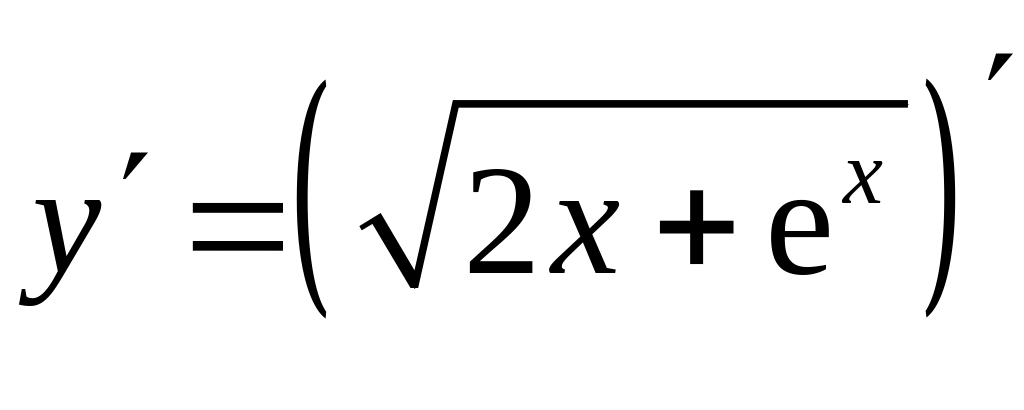 .
Под знаком производной стоит сложная
функция вида
.
Под знаком производной стоит сложная
функция вида
![]() ,
где
,
где
![]() – внутренняя функция. Используем
табличную формулу 7 для нахождения
производной степенной функции (см.
раздел Справочный
материал, Правила
дифференцирования. Таблица производных),
получим:
– внутренняя функция. Используем
табличную формулу 7 для нахождения
производной степенной функции (см.
раздел Справочный
материал, Правила
дифференцирования. Таблица производных),
получим:
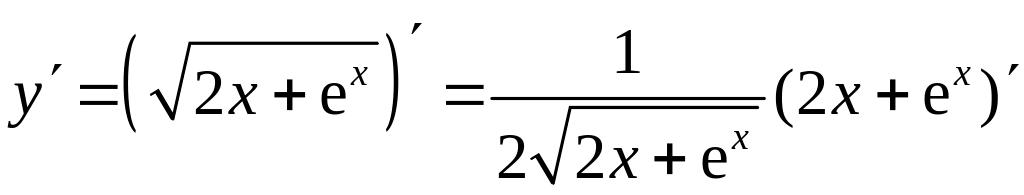 .
.
Для нахождения производной внутренней функции используем табличные формулы 1, 5, 6, 12 (см. раздел Справочный материал, Правила дифференцирования. Таблица производных), получим:
![]() .
.
Тогда
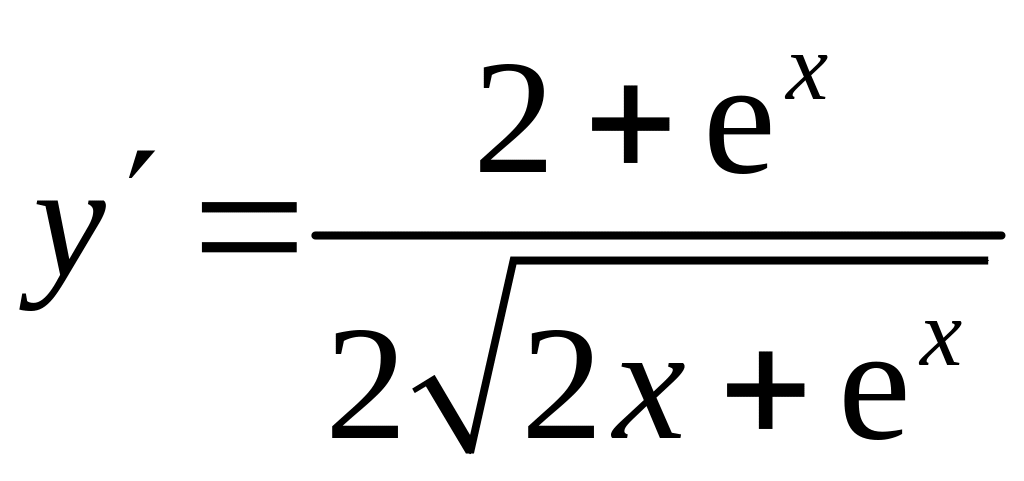 .
.
е)
Требуется найти
![]() .
Под знаком производной стоит произведение
постоянного множителя 2 на сложную
функцию вида
.
Под знаком производной стоит произведение
постоянного множителя 2 на сложную
функцию вида
![]() ,
где
,
где
![]() – внутренняя
функция. Используем табличную формулу
1 для нахождения производной произведения
постоянной на функцию и формулу 16 для
производной арктангенса (см.
раздел Справочный
материал, Правила
дифференцирования. Таблица производных),
получим:
– внутренняя
функция. Используем табличную формулу
1 для нахождения производной произведения
постоянной на функцию и формулу 16 для
производной арктангенса (см.
раздел Справочный
материал, Правила
дифференцирования. Таблица производных),
получим:
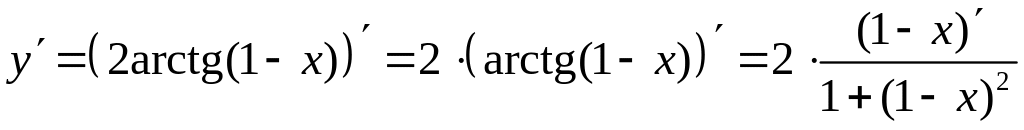 .
.
Для нахождения производной внутренней функции используем табличные формулы 2, 5, 6 (см. раздел Справочный материал, Правила дифференцирования. Таблица производных), получим:
![]() .
.
Тогда
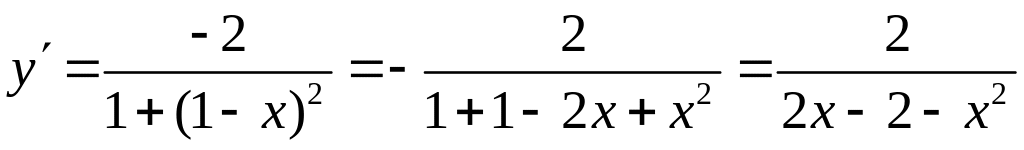 .
.
Пример 18. Найти производную первого порядка функции
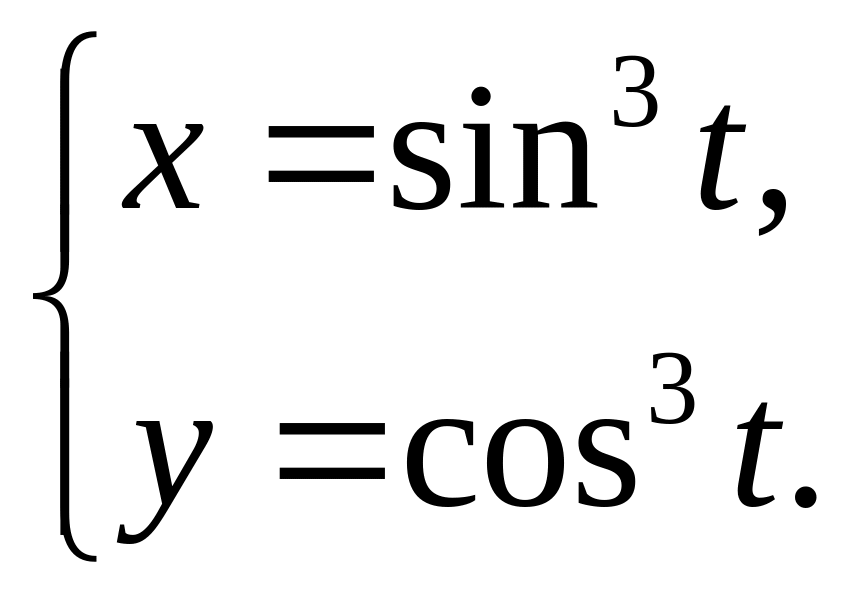
Решение. Имеем функцию, заданную параметрически. Для нахождения производной такой функции используем формулу:
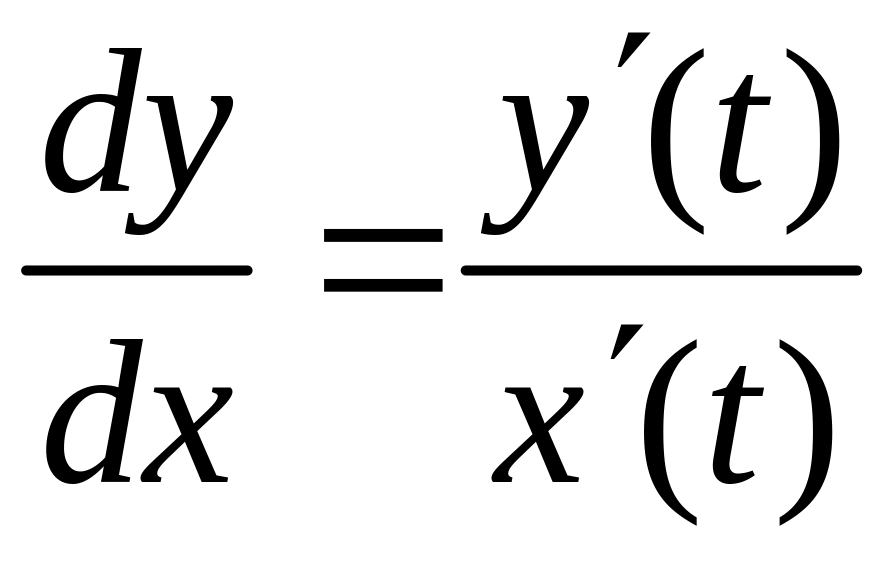 .
.
Чтобы
найти
![]() ,
используем табличные формулы 7 и 9
(см. раздел
Справочный
материал,
Правила
дифференцирования. Таблица производных):
,
используем табличные формулы 7 и 9
(см. раздел
Справочный
материал,
Правила
дифференцирования. Таблица производных):
![]() .
.
Чтобы
найти
![]() ,
используем табличные формулы 7 и 8
(см. раздел
Справочный
материал,
Правила
дифференцирования. Таблица производных):
,
используем табличные формулы 7 и 8
(см. раздел
Справочный
материал,
Правила
дифференцирования. Таблица производных):
![]() .
.
Тогда
 .
.
Пример 19. Найти производную первого порядка – функции
![]() .
.
Решение.
Имеем функцию, заданную неявно, т.е.
зависимость между аргументом
и функцией
задана уравнением, которое не разрешено
относительно
.
Чтобы найти производную такой функции,
нужно продифференцировать обе части
данного уравнения по переменной
,
считая
функцией, зависящей от
,
а затем выразить
![]() из полученного равенства. Имеем
из полученного равенства. Имеем
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Из последнего равенства выразим производную :
![]() ,
,
![]() ,
,
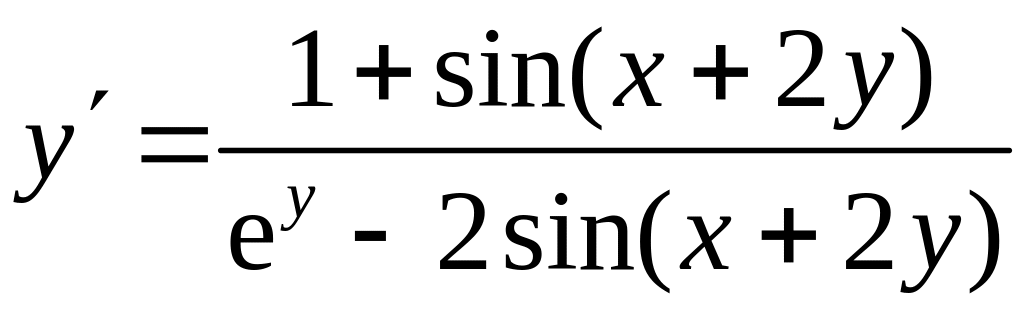 .
.
Пример 20. Найти производную первого порядка функции
![]() .
.
Решение. Имеем функцию, заданную неявно, т.е. зависимость между аргументом и функцией задана уравнением, которое не разрешено относительно . Чтобы найти производную такой функции, нужно продифференцировать обе части данного уравнения по переменной , считая функцией, зависящей от , а затем выразить из полученного равенства. Имеем:
![]() ,
,
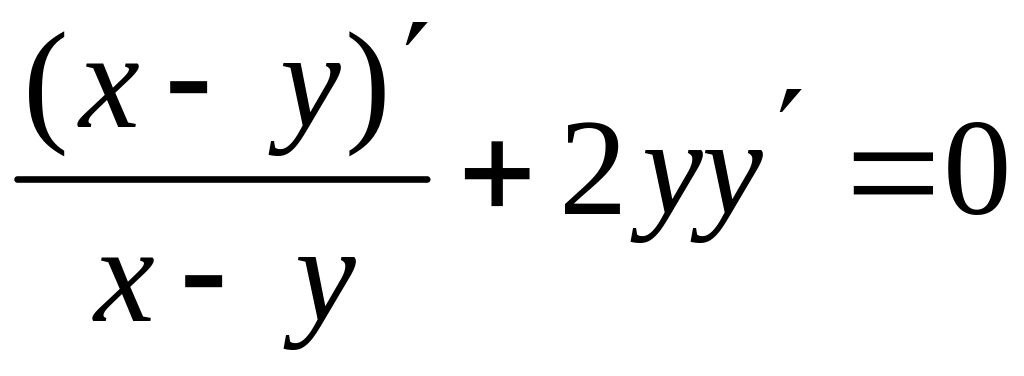 ,
,
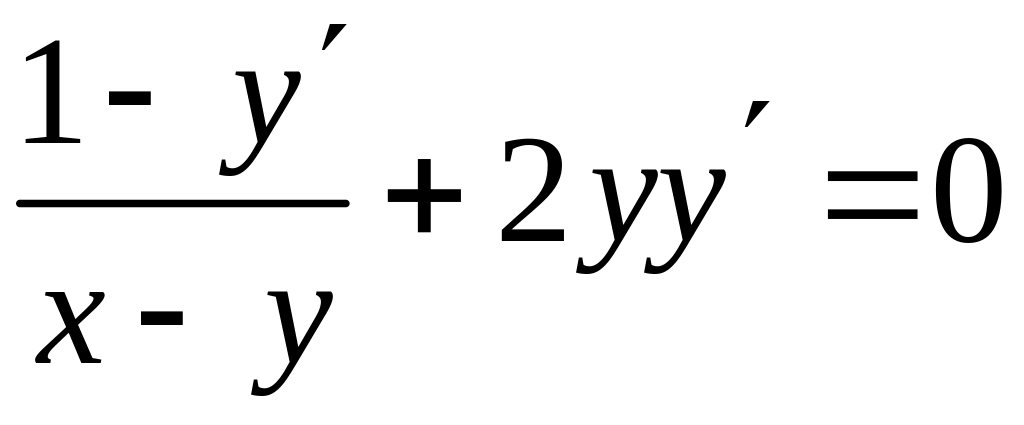 .
.
Из последнего равенства выразим производную :
 ,
,
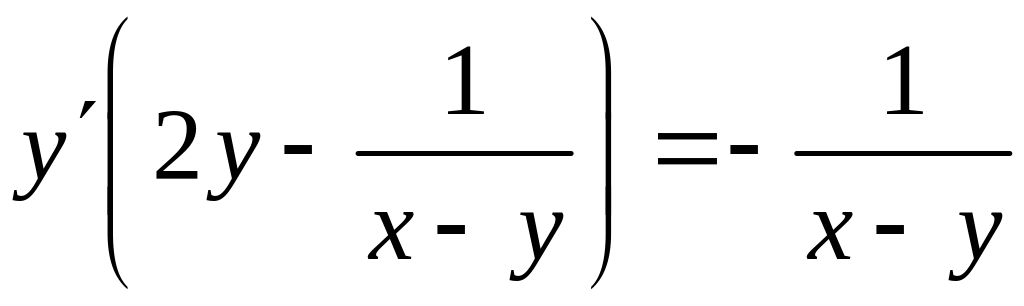 ,
,
 ,
,
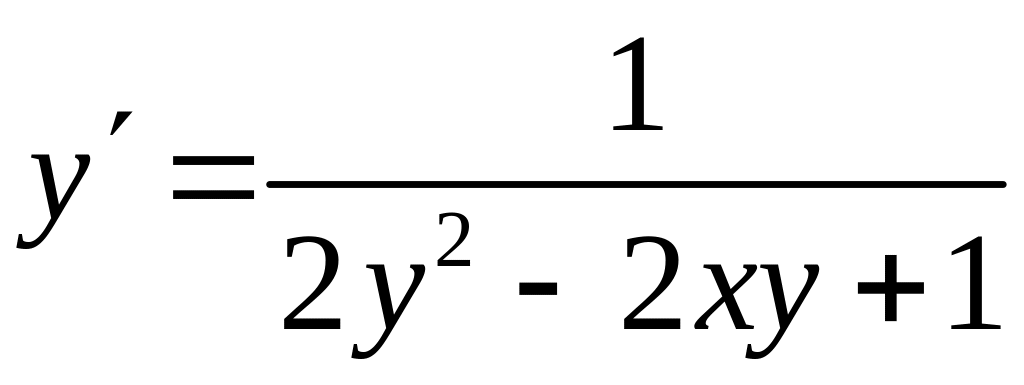 .
.
Пример 21. Найти приближенные значения указанных величин с помощью дифференциалов соответствующих функций:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Решение. а) Применим формулу для вычисления приближенного значения функции :
![]() ,
,
где
![]() – точка, в
которой требуется найти значение
функции;
– точка, в которой значение функции
определяется точно и которая близка к
;
– точка, в
которой требуется найти значение
функции;
– точка, в которой значение функции
определяется точно и которая близка к
;
![]() – значение производной функции в точке
;
– значение производной функции в точке
;
![]() – приращение аргумента.
– приращение аргумента.
В
данном задании функция
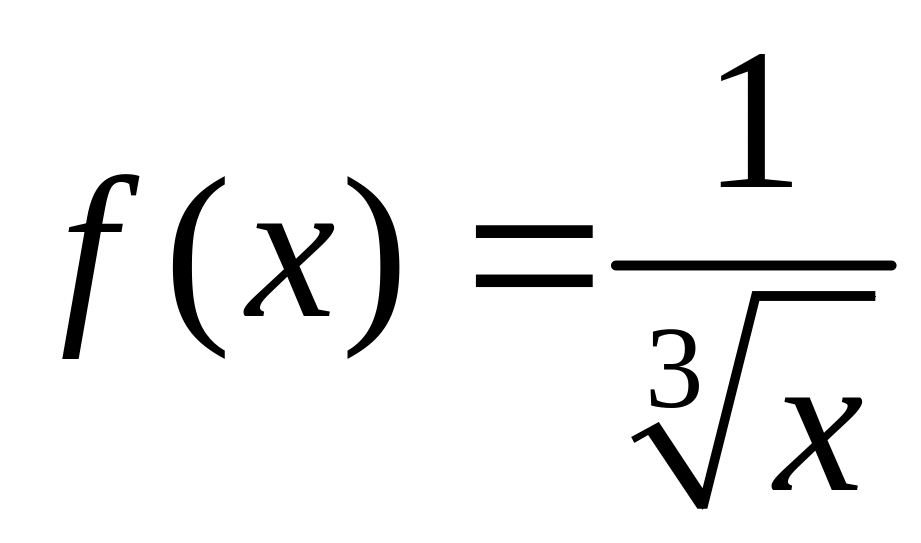 .
Требуется найти значение функции, когда
аргумент равен
.
Требуется найти значение функции, когда
аргумент равен
![]() .
Точка
.
Точка
![]() близка к 63 и в ней точно определяется
значение функции
:
близка к 63 и в ней точно определяется
значение функции
:
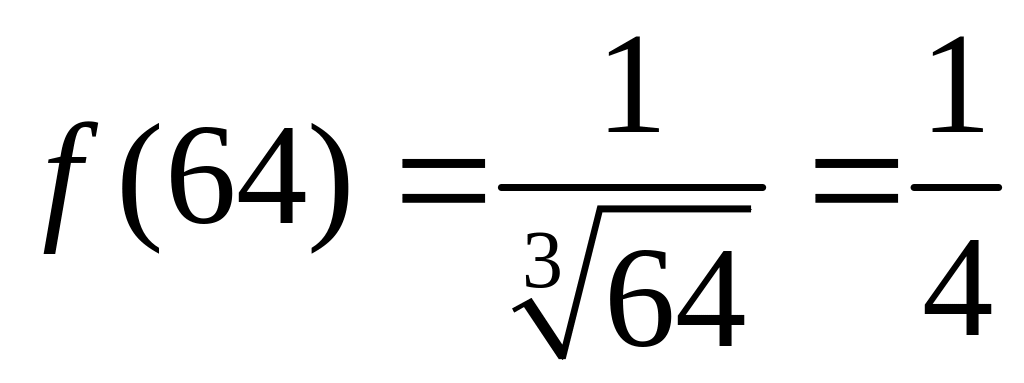 .
.
Найдем
производную функции
![]() :
:
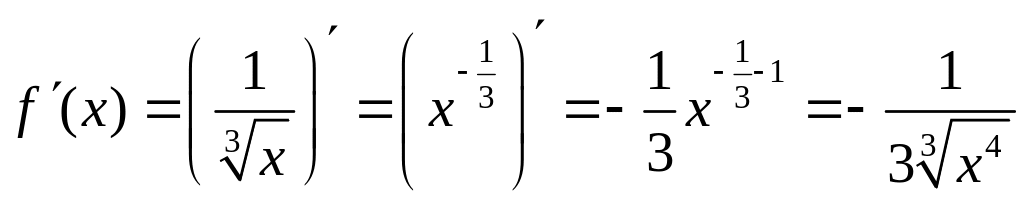 .
.
В точке производная функции
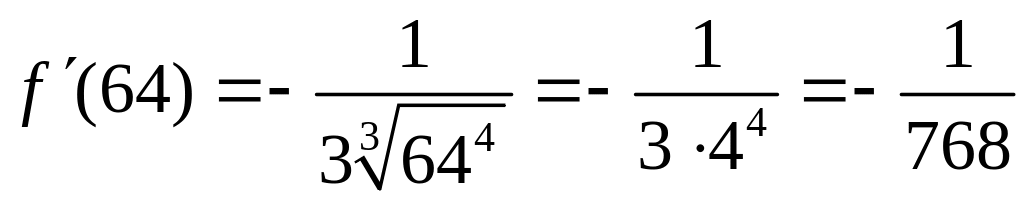 .
.
Найдем
приращение
из равенства
,
![]() .
Подставим найденное в формулу приближенного
вычисления и получим
.
Подставим найденное в формулу приближенного
вычисления и получим
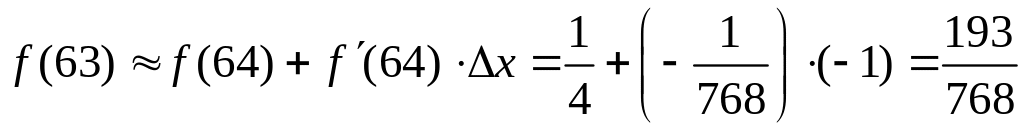 ,
,
т.е.
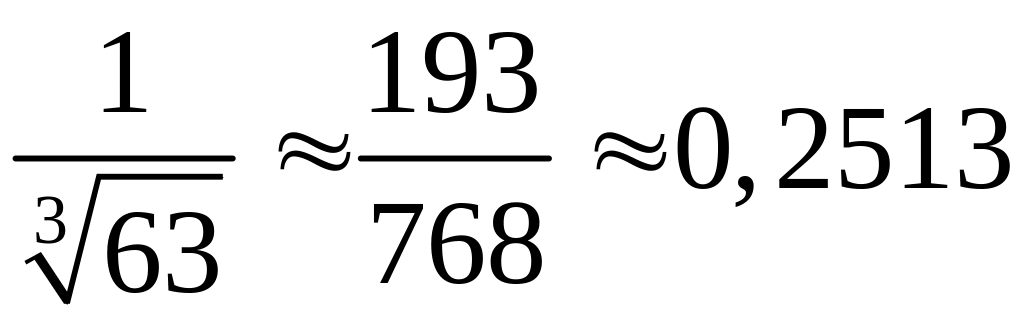 .
.
б) Применим формулу для вычисления приближенного значения функции :
,
где – точка, в которой требуется найти значение функции; – точка, в которой значение функции определяется точно и которая близка к ; – значение производной функции в точке ; – приращение аргумента.
В
данном задании функция
![]() .
Требуется найти значение функции, когда
аргумент
.
Требуется найти значение функции, когда
аргумент
![]() .
Точка
.
Точка
![]() близка к 0,9 и в ней точно определяется
значение функции
:
близка к 0,9 и в ней точно определяется
значение функции
:
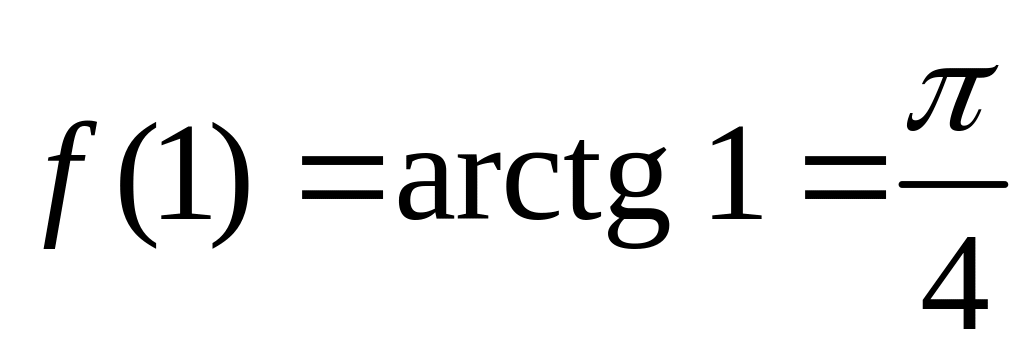 .
.
Найдем производную функции :
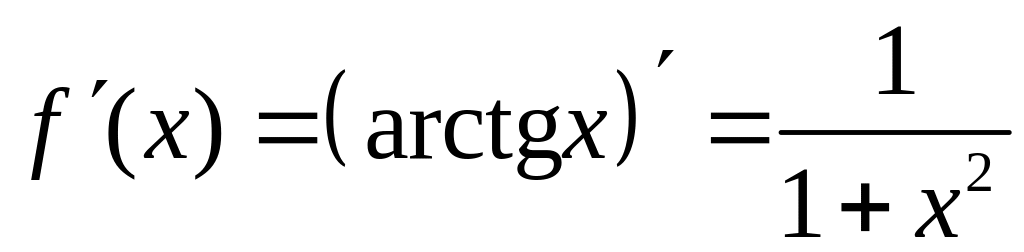 .
.
В точке производная функции
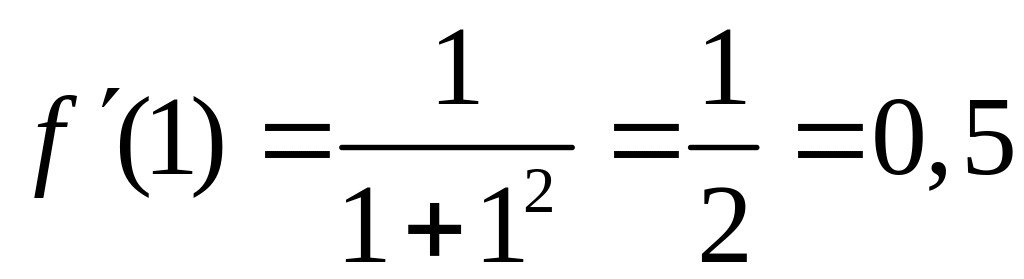 .
.
Найдем
приращение
из равенства
![]() .
Подставим найденное в формулу приближенного
вычисления и получим
.
Подставим найденное в формулу приближенного
вычисления и получим
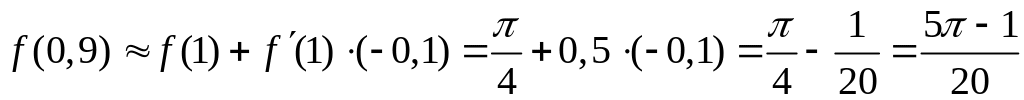 ,
,
т.е.
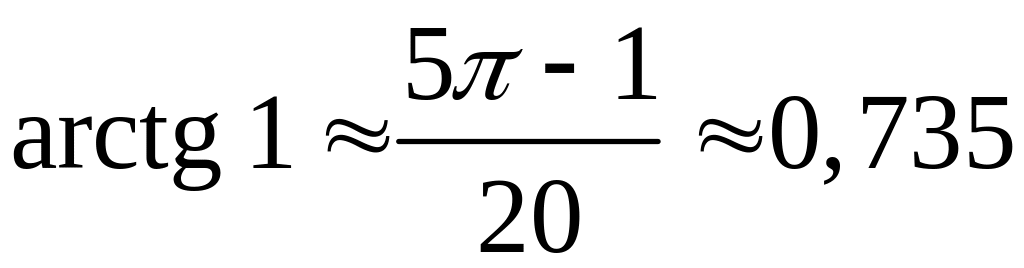 .
.
в) Применим формулу для вычисления приближенного значения функции :
,
где – точка, в которой требуется найти значение функции; – точка, в которой значение функции определяется точно и которая близка к ; – значение производной функции в точке ; – приращение аргумента.
В
данном задании функция
![]() .
Требуется найти значение функции, когда
аргумент
.
Требуется найти значение функции, когда
аргумент
![]() .
Точка
.
Точка
![]() близка к
близка к
![]() и в ней точно определяется значение
функции
:
и в ней точно определяется значение
функции
:
![]() .
.
Найдем производную функции :
![]() .
.
В точке производная функции
![]() .
.
Найдем
приращение
из равенства
,
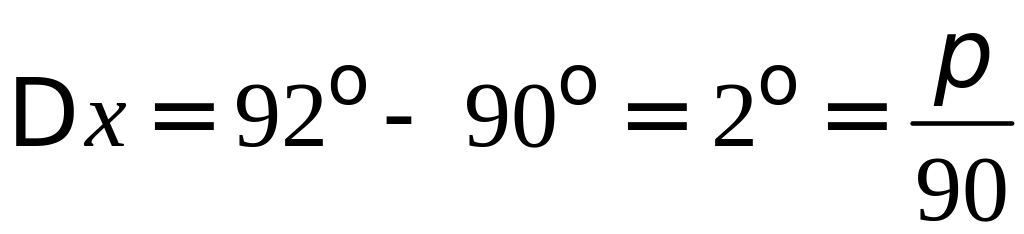 .
Подставим найденное в формулу приближенного
вычисления и получим
.
Подставим найденное в формулу приближенного
вычисления и получим
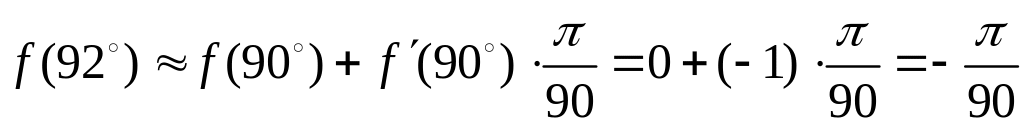 ,
,
т.е.
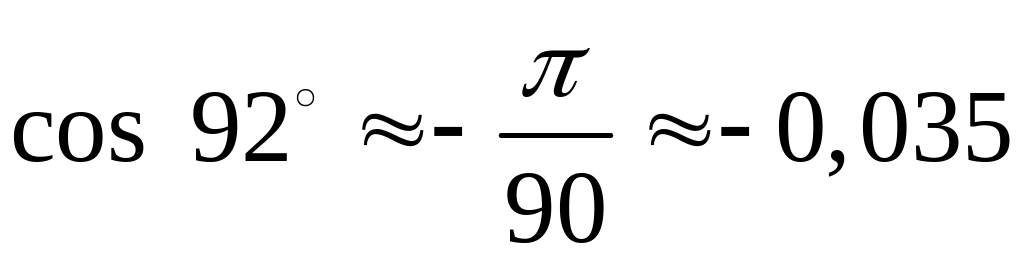 .
.
Пример 22. Требуется исследовать данные функции методами дифференциального исчисления и построить их графики:
а)
 ;
б)
;
б)
 .
.
При исследовании функций будем придерживаться следующей схемы.
Найти область определения функции.
Указать специальные свойства функции (четность/ нечетность, периодичность).
Указать область непрерывности функции, наличие точек разрыва и вертикальных асимптот.
Найти горизонтальные и наклонные асимптоты (если они есть).
Найти промежутки возрастания, убывания функции и ее точки экстремума.
Найти промежутки выпуклости, вогнутости графика функции и точки перегиба.
Найти точки пересечения графика функции с осями координат, дополнительные точки.
Построить график функции, используя полученные результаты.
Решение.
а) 1. Данная функция
является дробно-рациональной, значит,
она определена при всех действительных
значениях переменной
,
кроме нулей знаменателя. Знаменатель
обращается в 0, если
![]() ,
т.е.
,
т.е.
![]() .
Запишем область определения функции
.
Запишем область определения функции
![]() .
.
2. Проверим, является ли данная функция четной или нечетной. Найдем
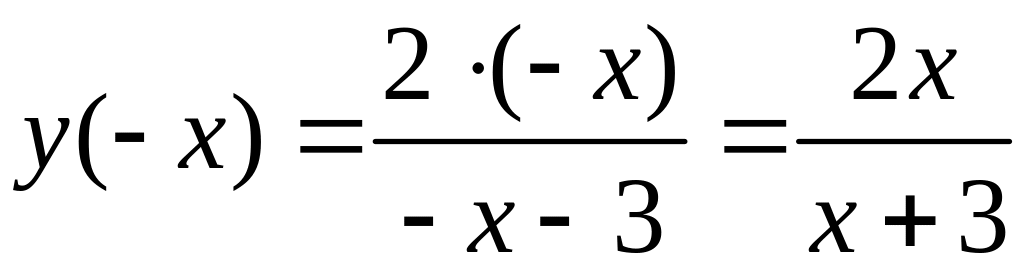 .
.
Т.к.
![]() ,
то функция не является четной. Т.к.
,
то функция не является четной. Т.к.
![]() ,
то функция не является нечетной. Данная
функция не является периодической.
,
то функция не является нечетной. Данная
функция не является периодической.
3.
Данная функция является непрерывной
на всей своей области определения, т.е.
при
![]() .
Точка
является точкой разрыва данной функции,
т.к. функция в ней не определена. Найдем
односторонние пределы функции в этой
точке:
.
Точка
является точкой разрыва данной функции,
т.к. функция в ней не определена. Найдем
односторонние пределы функции в этой
точке:
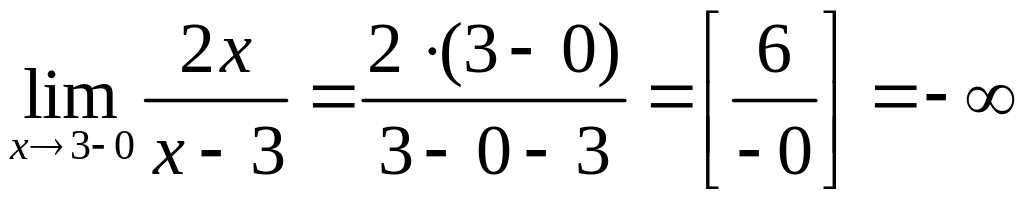 ,
,
 .
.
Т.к. односторонние пределы бесконечны, то прямая является вертикальной асимптотой графика функции.
4.
Уравнение наклонной или горизонтальной
асимптоты графика функции имеет вид
![]() ,
где
и
,
где
и
![]() находятся по формулам:
находятся по формулам:
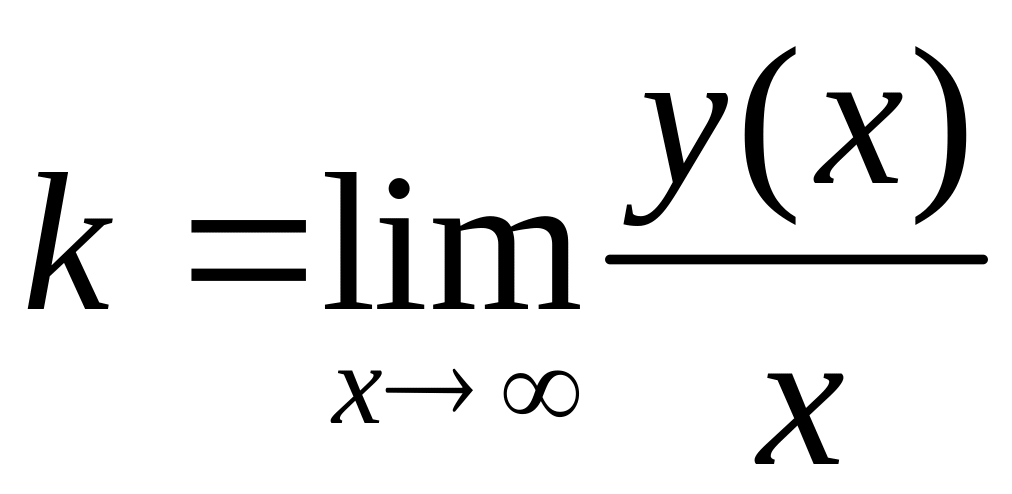 ,
,
![]() .
.
Для данной функции
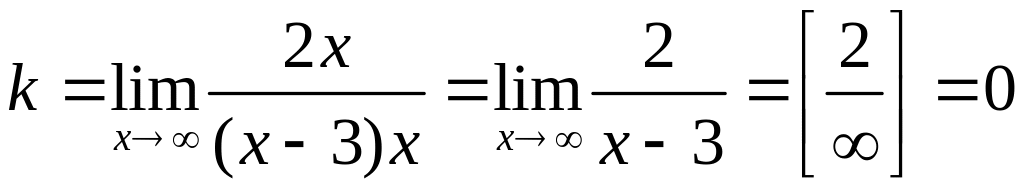 ,
,
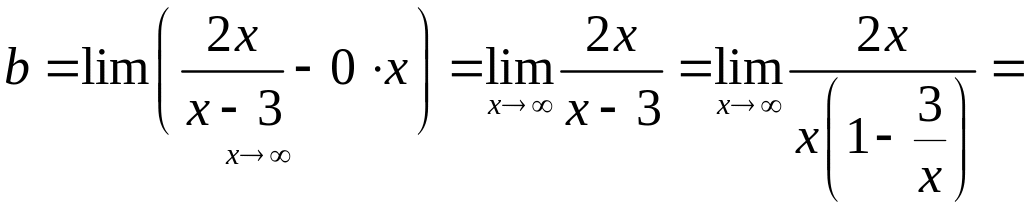
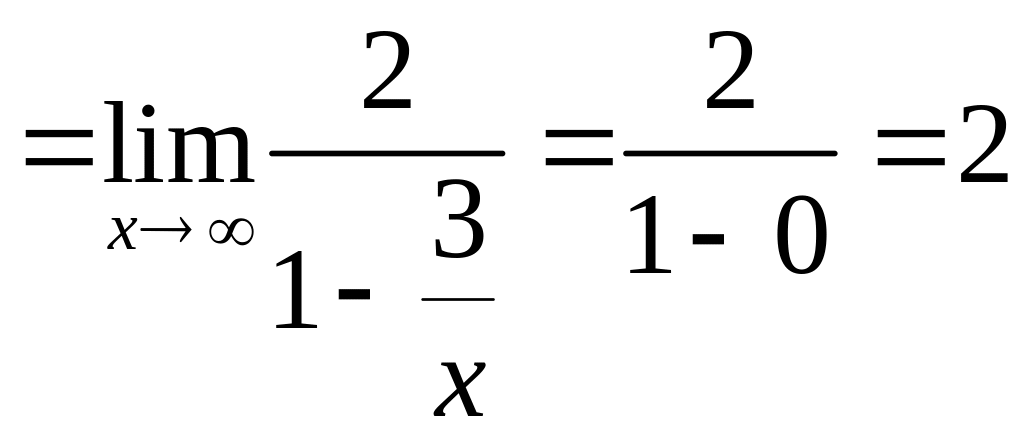 .
.
Имеем
![]() ,
,
![]() ,
тогда уравнение асимптоты
,
тогда уравнение асимптоты
![]() .
Это горизонтальная асимптота, т.к.
.
Это горизонтальная асимптота, т.к.
![]() .
.
5. Найдем производную функции
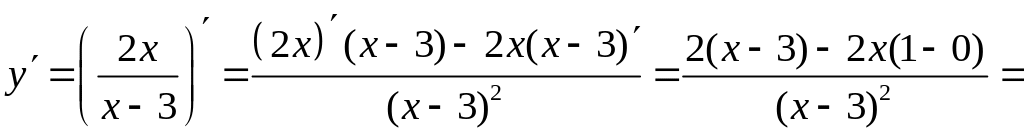
 .
.
Производная
непрерывна и отлична от 0 на всей области
определения функции
![]() .
Значит, функция не имеет точек,
подозрительных на экстремум. Определим
знак производной на каждом из интервалов,
составляющих область определения:
.
Значит, функция не имеет точек,
подозрительных на экстремум. Определим
знак производной на каждом из интервалов,
составляющих область определения:
![]() и
и
![]() .
Для этого найдем значение производной
в каких–либо произвольных точках этих
интервалов.
.
Для этого найдем значение производной
в каких–либо произвольных точках этих
интервалов.
Например,
 ,
,
значит, функция убывает на промежутке ;
 ,
,
значит, функция убывает на промежутке . По результатам вычислений заполним таблицу 3.
Таблица 3
|
|
|
|
|
|
|
|
|
6. Найдем вторую производную функции.
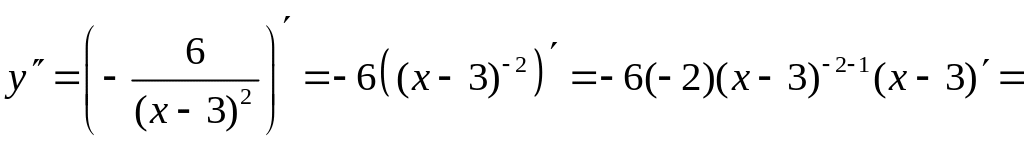
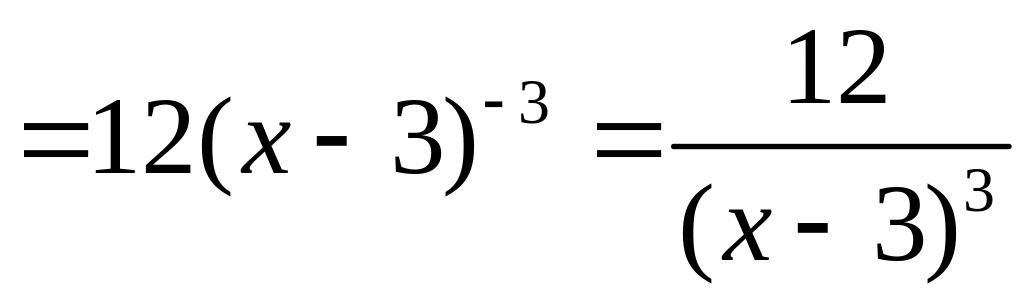 .
.
Вторая производная непрерывна и отлична от 0 на всей области определения функции .
Значит, кривая не имеет точек, подозрительных на перегиб.
Определим знак второй производной на каждом из интервалов, составляющих область определения: и .
Для этого найдем значение второй производной в каких–либо произвольных точках этих интервалов.
Например,
 ,
,
значит, кривая выпукла вверх на промежутке ;
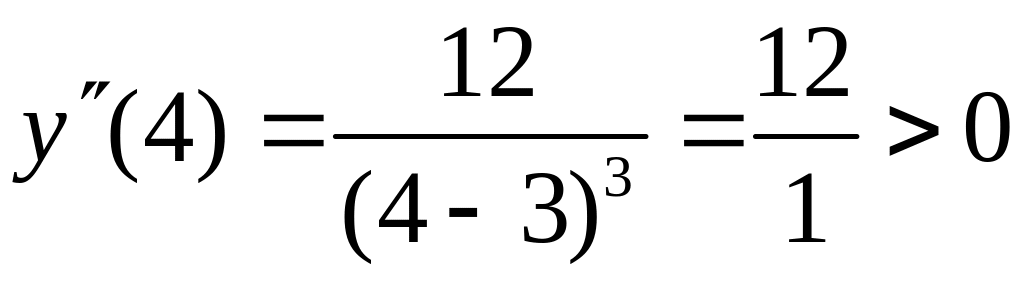 ,
,
значит, кривая выпукла вниз на промежутке .
По результатам вычислений заполним таблицу 4.
Таблица 4
|
|
|
|
|
|
|
|
|
Объединим результаты пп. 5 и 6 на схеме (см. рис. 12).

Р и с. 12
7. Найдем точки пересечения графика функции с осями координат.
С
осью
:
,
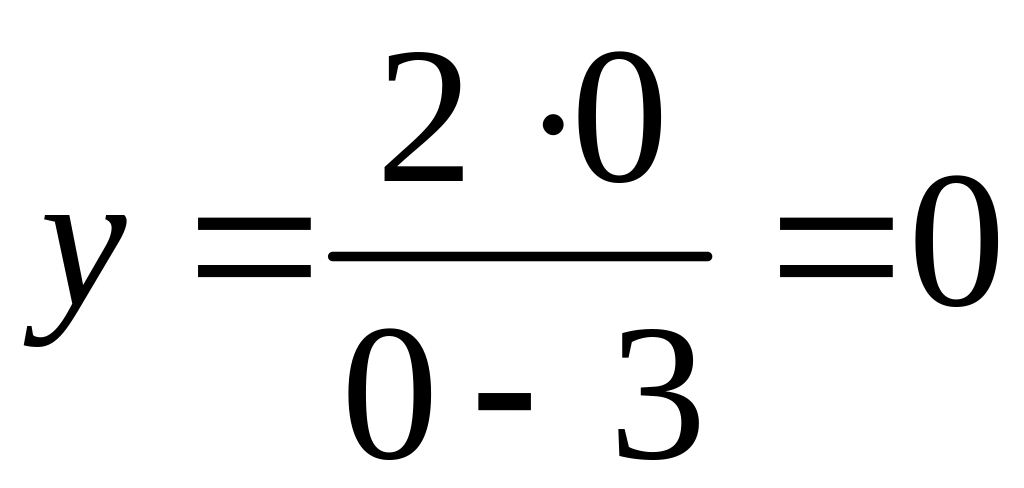 ,
точка
,
точка
![]() .
С осью
:
.
С осью
:
![]() ,
,
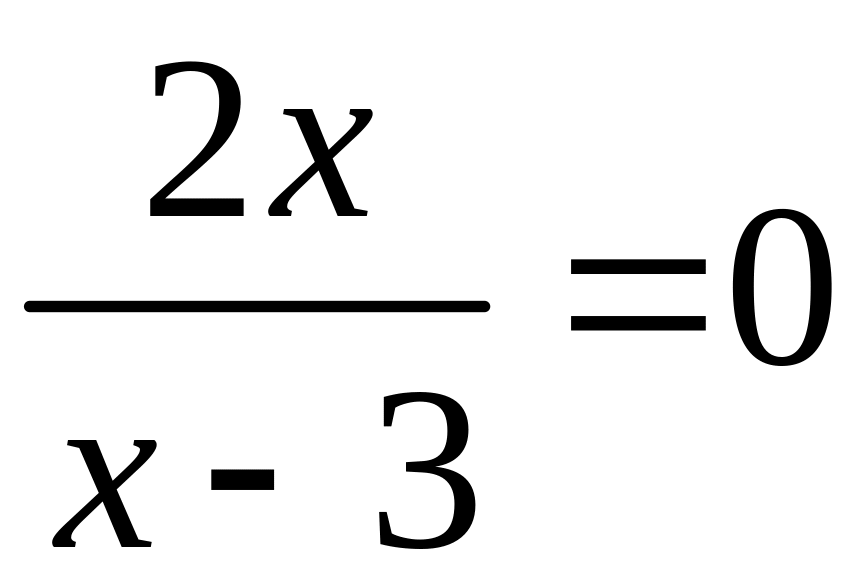 ,
откуда
,
точка
.
,
откуда
,
точка
.
Дополнительные
точки для построения графика:
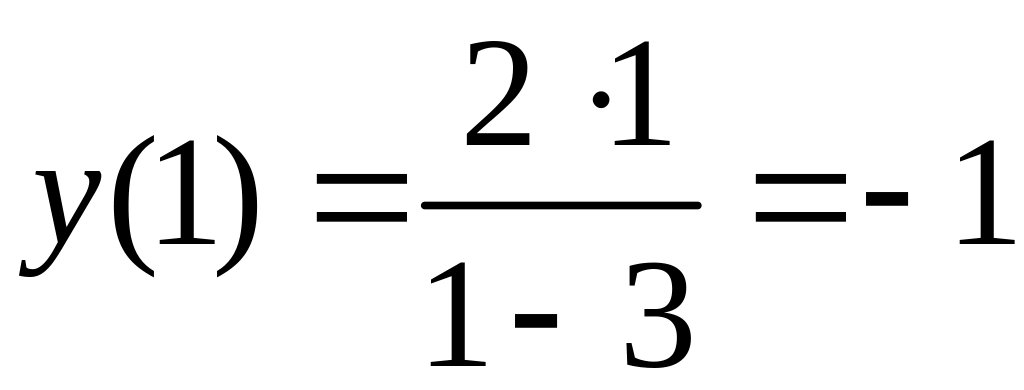 ,
точка
,
точка
![]() ;
;
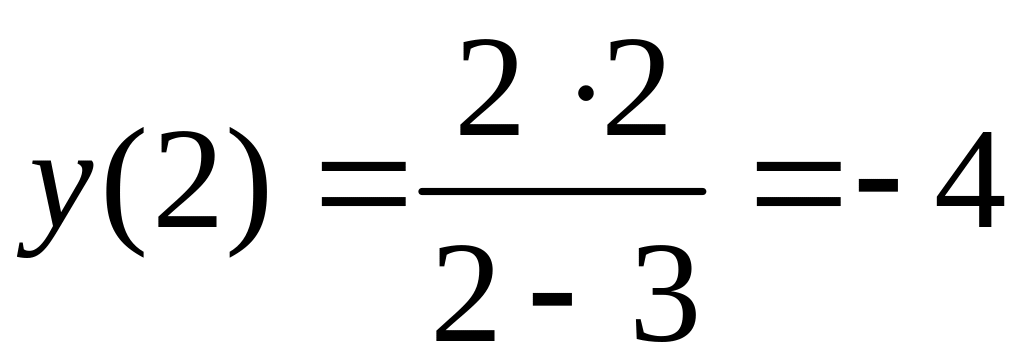 ,
точка
,
точка
![]() ;
;
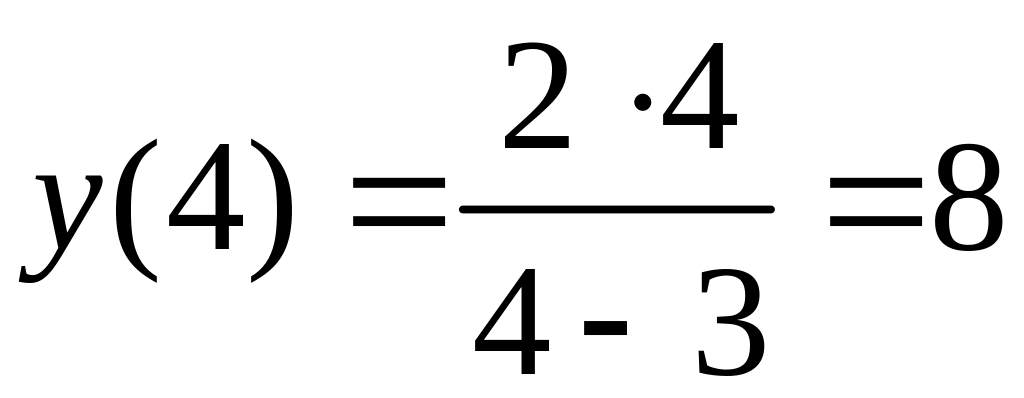 ,
точка
,
точка
![]() ;
;
 ,
точка
,
точка
![]() ;
;
 ,
точка
,
точка
![]() .
.
8. Построим график функции.
Сначала проведем на чертеже вертикальную асимптоту графика функции и горизонтальную асимптоту .
Затем выполним построение самой кривой (см. рис. 13), учитывая результаты пунктов 5–7.

Р и с. 13
б)
1. Данная функция
является целой рациональной, значит,
она определена при всех действительных
значениях переменной
.
Запишем область определения функции
![]() .
.
2. Проверим, является ли данная функция четной или нечетной. Найдем
 .
.
Так как , то функция не является четной. Так как , то функция не является нечетной. Данная функция не является периодической.
3. Данная функция является непрерывной на всей своей области определения, т.е. при . Точек разрыва функция не имеет, значит, у ее графика нет вертикальных асимптот.
4. Уравнение наклонной или горизонтальной асимптоты графика функции имеет вид , где и находятся по формулам
, .
Для данной функции
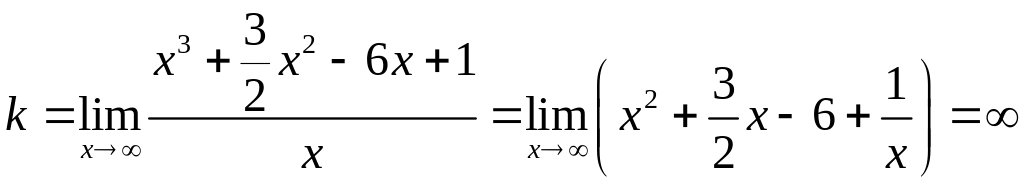 .
.
Так как коэффициент бесконечен, то график данной функции не имеет наклонных и горизонтальной асимптот.
5. Найдем производную функции
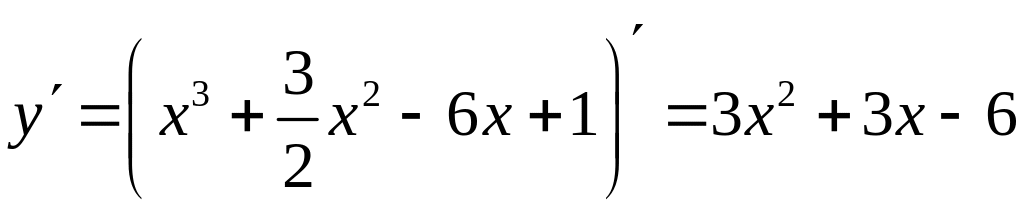 .
.
Производная непрерывна на всей области определения функции . Выясним, если точки, в которых производная обращается в 0. Решим уравнение
![]() ,
,
![]()
![]() ,
,
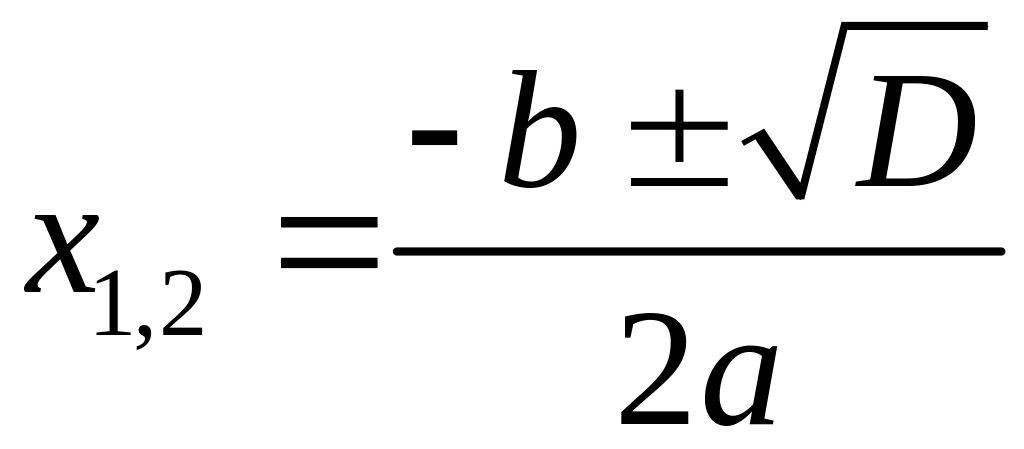 ,
,
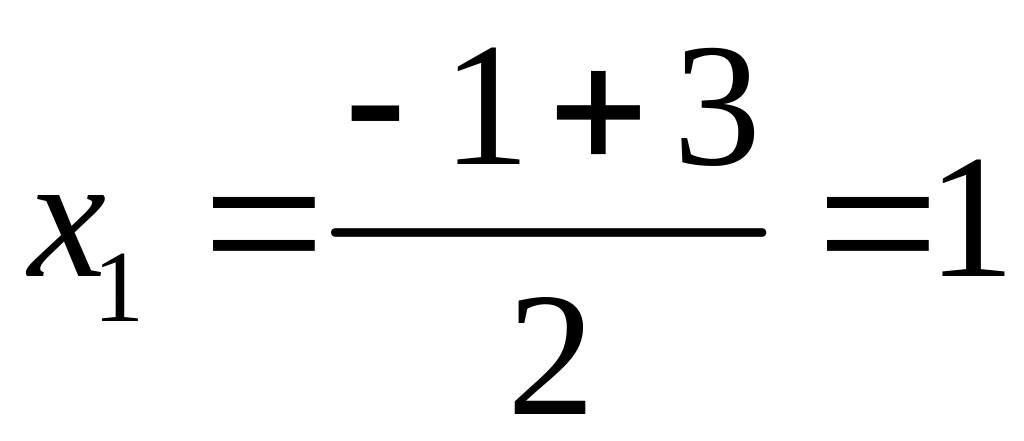 ,
,
 .
.
Значит,
функция имеет две точки, подозрительные
на экстремум. Определим знак производной
на каждом из интервалов, на которые эти
точки разбивают область определения
функции:
,
![]() и
и
![]() .
.
Для этого найдем значение производной в каких–либо произвольных точках этих интервалов. Например,
![]() ,
,
значит, функция возрастает на промежутке ;
![]() ,
,
значит, функция убывает на промежутке ;
![]() ,
,
значит, функция возрастает на промежутке . Точка является точкой максимума, точка – точкой минимума функции. По результатам вычислений заполним таблицу 5.
Таблица 5
|
|
|
|
1 |
|
|
>0 |
0 |
<0 |
0 |
>0 |
|
|
11 |
|
|
|
|
|
|
|
|
|
6. Найдем вторую производную функции
![]() .
.
Вторая производная непрерывна на всей области определения функции . Найдем точки, в которых вторая производная равна 0.
![]() ,
,
![]()
Значит,
точка кривой с абсциссой
— точка, подозрительная на перегиб.
Определим знак второй производной на
каждом из интервалов, на которые
разбивается область определения точкой
:
![]() и
и
![]() .
Для этого найдем значение второй
производной в каких–либо произвольных
точках этих интервалов. Например,
.
Для этого найдем значение второй
производной в каких–либо произвольных
точках этих интервалов. Например,
![]() ,
,
значит, кривая выпукла вверх на промежутке ;
![]() ,
,
значит, кривая выпукла вниз на промежутке . По результатам вычислений заполним таблицу 6.
Таблица 6
|
|
|
|
|
|
0 |
|
|
|
4,25 |
|
Объединим результаты пп. 5 и 6 на схеме (см. рис. 14).

Р и с. 14
7.
Найдем точки пересечения графика функции
с осью
:
,
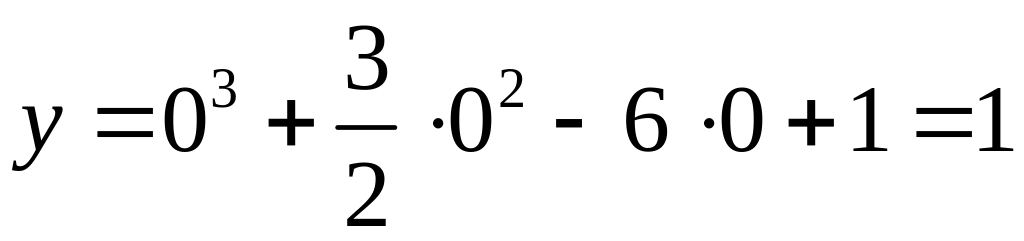 ,
точка
,
точка
![]() .
Дополнительные точки для построения
графика:
.
Дополнительные точки для построения
графика:
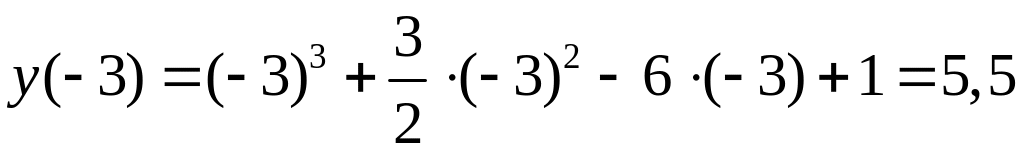 ,
точка
,
точка
![]() ;
;
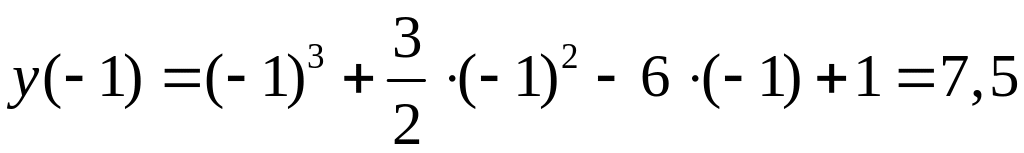 ,
точка
,
точка
![]() ;
;
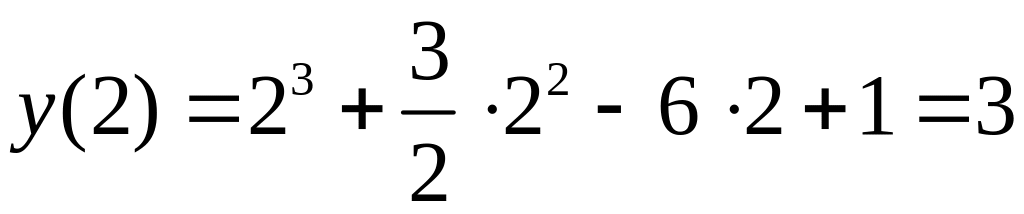 ,
точка
,
точка
![]() .
.
8. Построим график функции, учитывая результаты предыдущих пунктов (см. рис. 15).

Р и с. 15
В примере 23 нам понадобится следующая теорема ([8], т.1).
Теорема
Вейерштрасса.
Непрерывная на отрезке
![]() функция достигает на этом отрезке по
меньшей мере один раз наибольшего
значения
и
наименьшего значения
функция достигает на этом отрезке по
меньшей мере один раз наибольшего
значения
и
наименьшего значения
![]() .
.
Пример
23. Найти
наибольшее и наименьшее значения функции
![]() на заданном отрезке:
на заданном отрезке:
а)
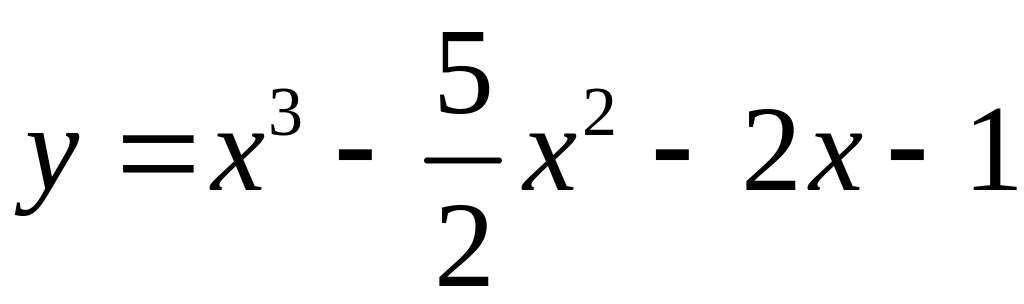 ,
,
![]() ;
;
б)
![]() ,
,
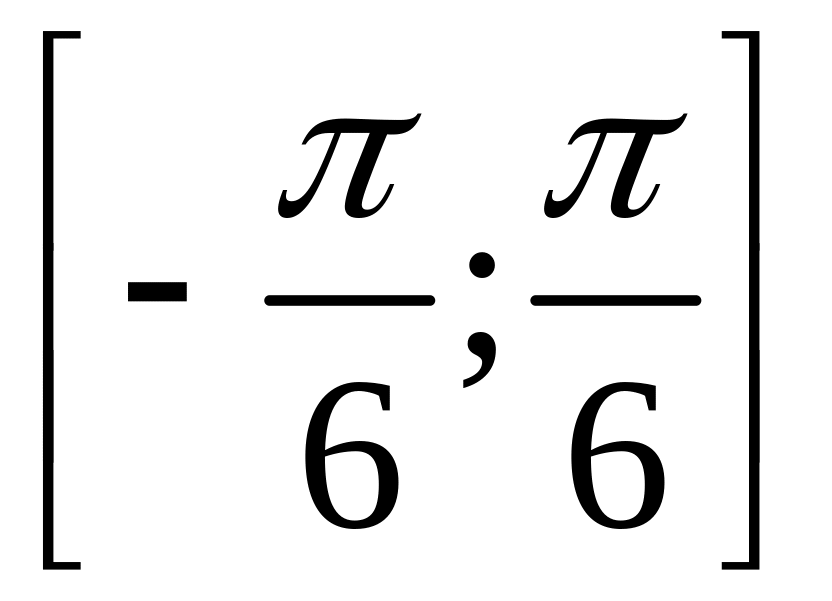 ;
;
в)
![]() ,
,
![]() .
.
Решение. Исследовать функцию на наибольшее и наименьшее значения на отрезке будем по следующей схеме.
Установить непрерывность функции на заданном отрезке.
Сделать вывод по теореме Вейерштрасса о существовании наибольшего и наименьшего значений.
Найти производную функции. Найти точки, подозрительные на экстремум (т.е. точки, в которых производная не существует или равна нулю), и выбрать из них те, которые принадлежат отрезку.
Вычислить значения функции на концах отрезка и в точках, найденных в пункте 2. Из полученных значений выбрать наибольшее и наименьшее и дать ответ.
а) 1. Функция является целой рациональной и непрерывна на всей числовой оси, а значит и на отрезке . Следовательно, по теореме Вейерштрасса существует наибольшее и наименьшее значения функции на этом отрезке.
2. Найдем производную функции:
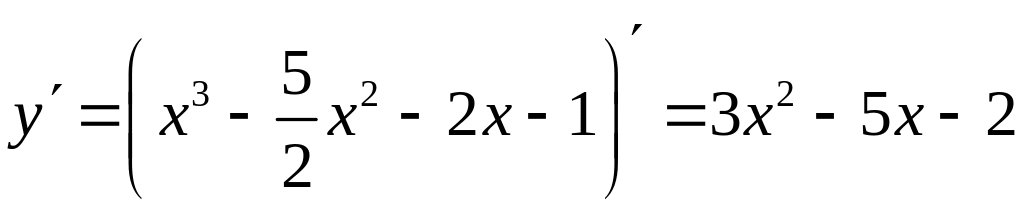 .
.
Производная функции непрерывна на всей числовой оси, а значит и на отрезке . Найдем точки, в которых она обращается в 0.
![]() ,
,
![]() ,
,
 ,
,
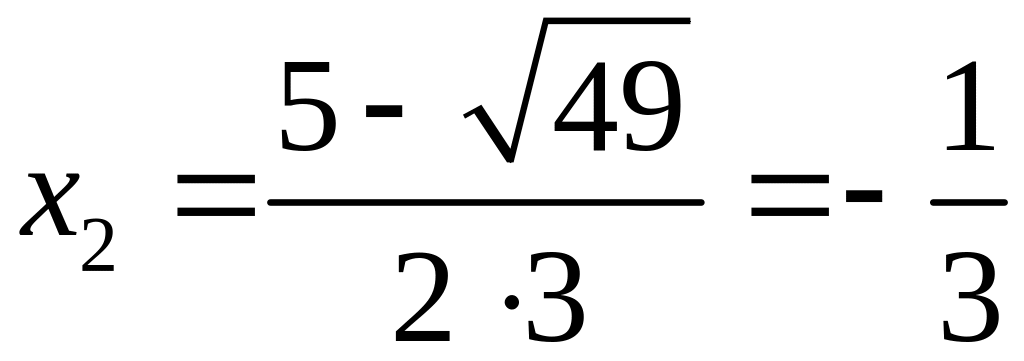 .
.
Из
двух найденных точек, подозрительных
на экстремум, только
![]() принадлежит отрезку
.
принадлежит отрезку
.
3. Вычислим значения функции на концах заданного отрезка и в точке :
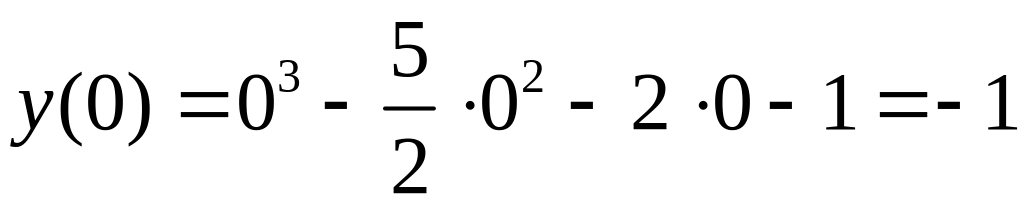 ,
,
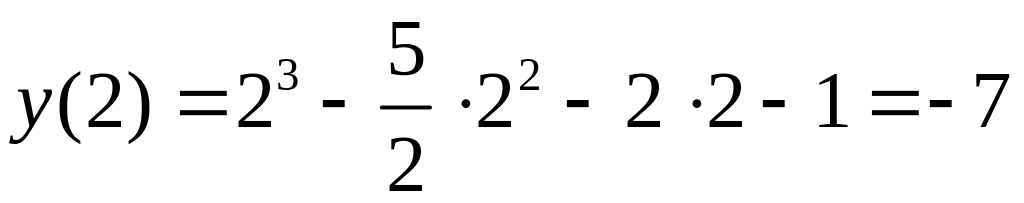 ,
,
 .
.
Из найденных значений выберем наибольшее и наименьшее:
![]() ,
,
![]() .
.
б) 1. Функция является разностью целой рациональной функции и тригонометрической функции синус, следовательно, она непрерывна на всей числовой оси, а значит и на отрезке . Следовательно, по теореме Вейерштрасса существует наибольшее и наименьшее значения функции на этом отрезке.
2. Найдем производную функции:
![]() .
.
Производная функции непрерывна на всей числовой оси, а значит и на отрезке . Найдем точки, в которых она обращается в 0.
![]() ;
;
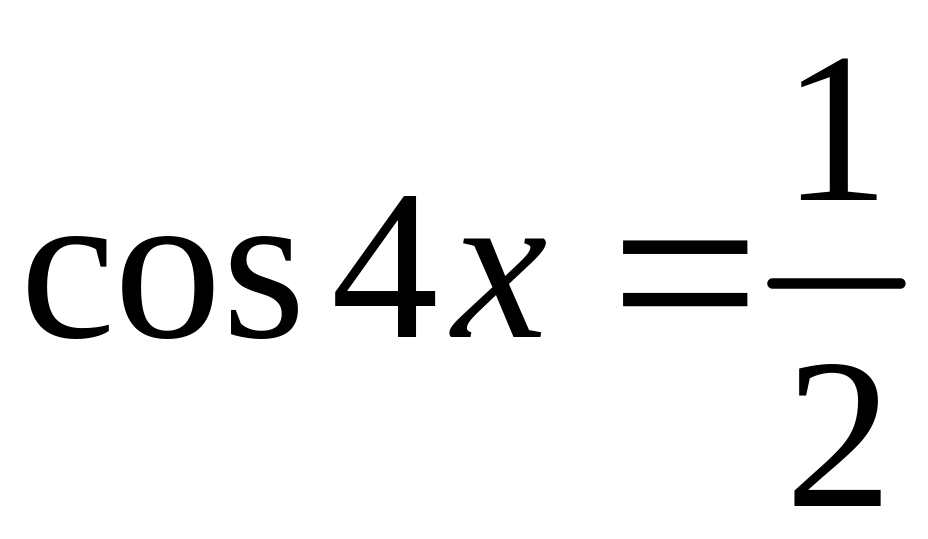 ;
;
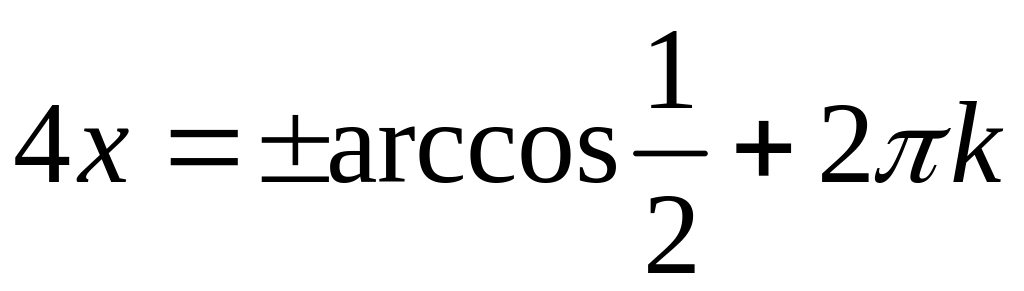 ,
,
![]() ;
;
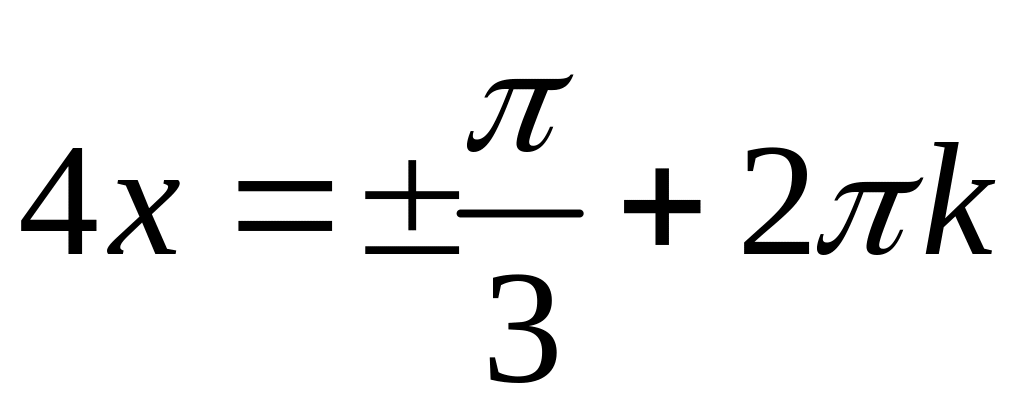 ,
;
,
;
 ,
.
,
.
Из
найденных точек, подозрительных на
экстремум, только
![]() и
и
![]() принадлежат отрезку
.
принадлежат отрезку
.
3. Вычислим значения функции на концах заданного отрезка и в точках , :
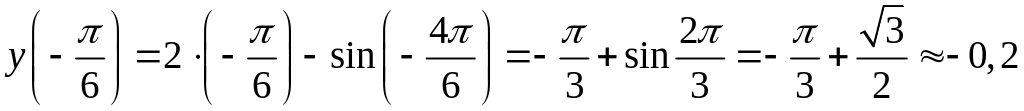
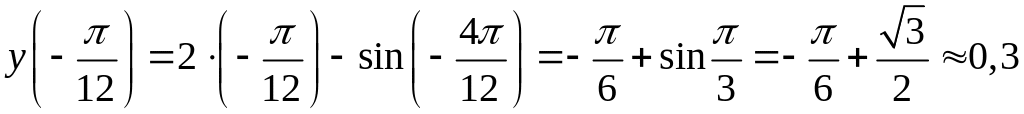 ,
,
 ,
,
 .
.
Из найденных значений выберем наибольшее и наименьшее:
 ,
,
 .
.
в)
1. Функция
является
разностью иррациональной и логарифмической
функций. Иррациональная функция
непрерывна при неотрицательных значениях
аргумента, логарифмическая функция
непрерывна при положительных значениях
аргумента, значит, сама функция
непрерывна при
![]() .
Заданный отрезок
.
Заданный отрезок
![]() входит в область непрерывности функции.
Следовательно, по теореме Вейерштрасса
существует наибольшее и наименьшее
значения функции на этом отрезке.
входит в область непрерывности функции.
Следовательно, по теореме Вейерштрасса
существует наибольшее и наименьшее
значения функции на этом отрезке.
2. Найдем производную функции:
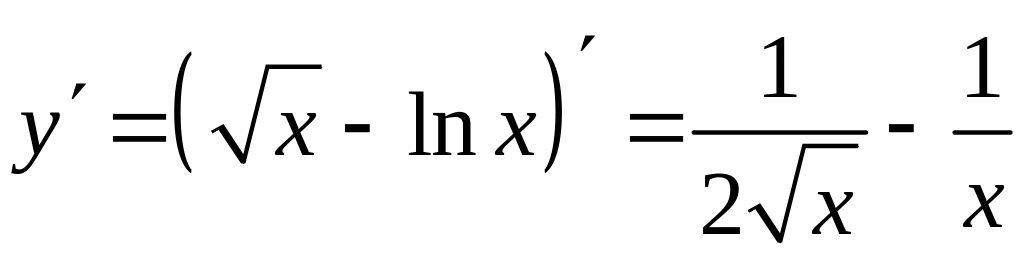 .
.
Производная функции непрерывна при , а значит и на отрезке . Найдем точки, в которых она обращается в 0.
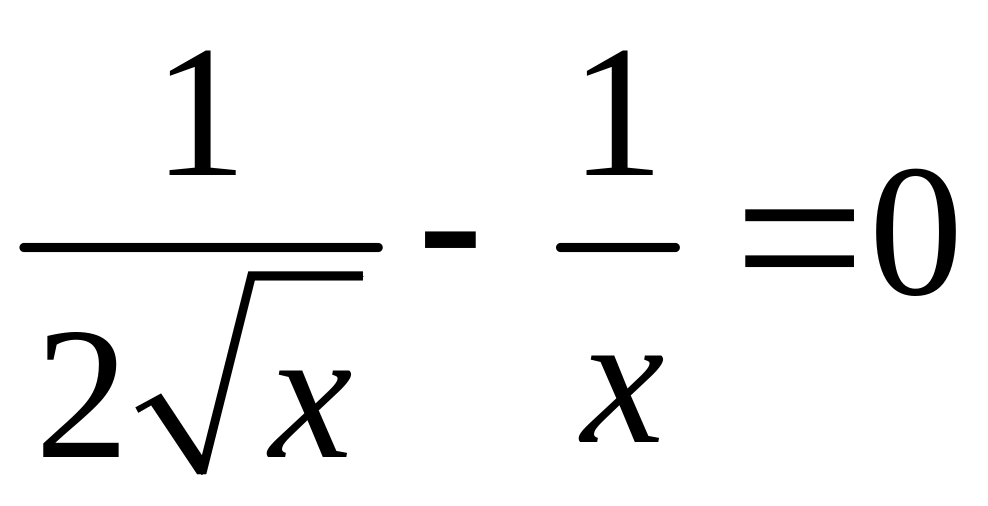 ,
,
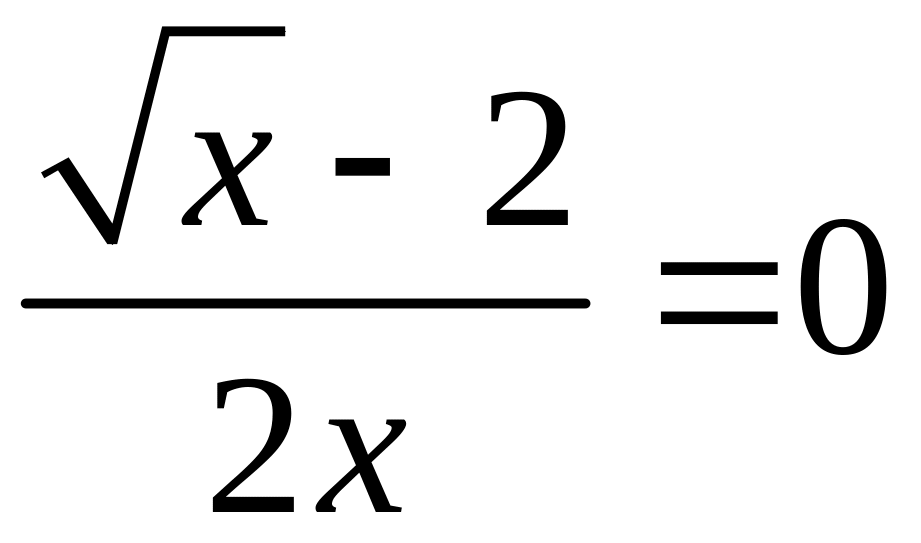 ,
,
![]() ,
,
![]() .
.
Найденная точка, подозрительная на экстремум, не принадлежит заданному отрезку и в дальнейшем рассматриваться не будет.
3. Вычислим значения функции на концах заданного отрезка:
![]() ,
,
![]() .
.
Из найденных значений выберем наибольшее и наименьшее:
![]() ,
,
![]() .
.
Пример 24. Найти неопределенные интегралы методом замены переменной:
a)
![]() ;
б)
;
б)
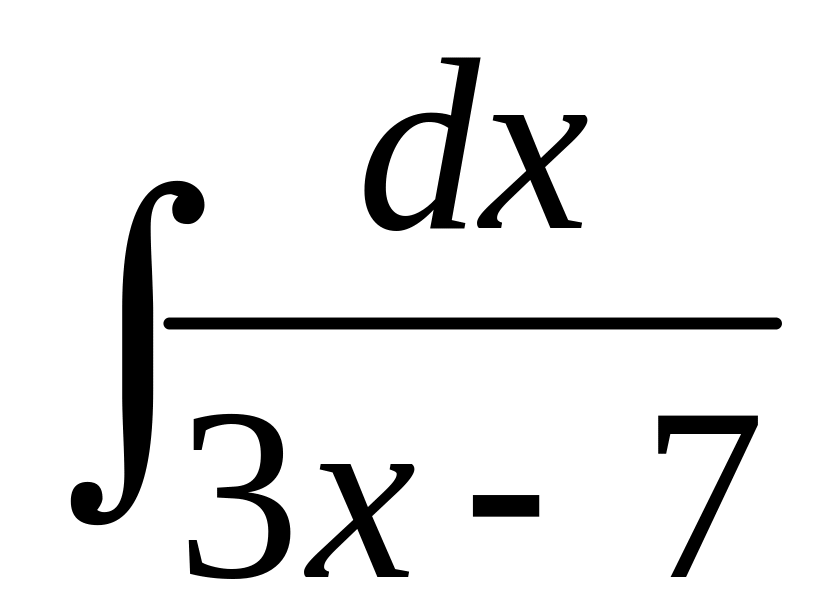
в)
![]() ;
г)
;
г)
 ;
;
д)
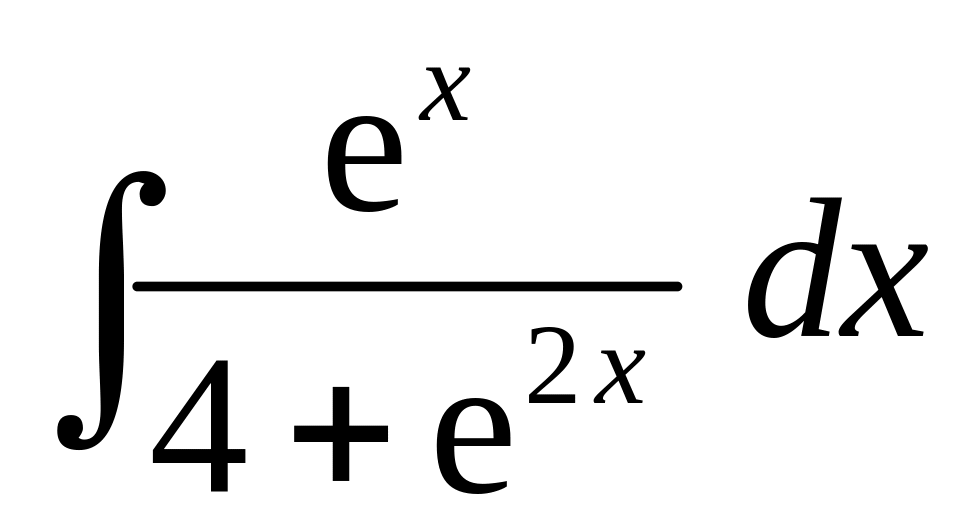 ;
е)
;
е)
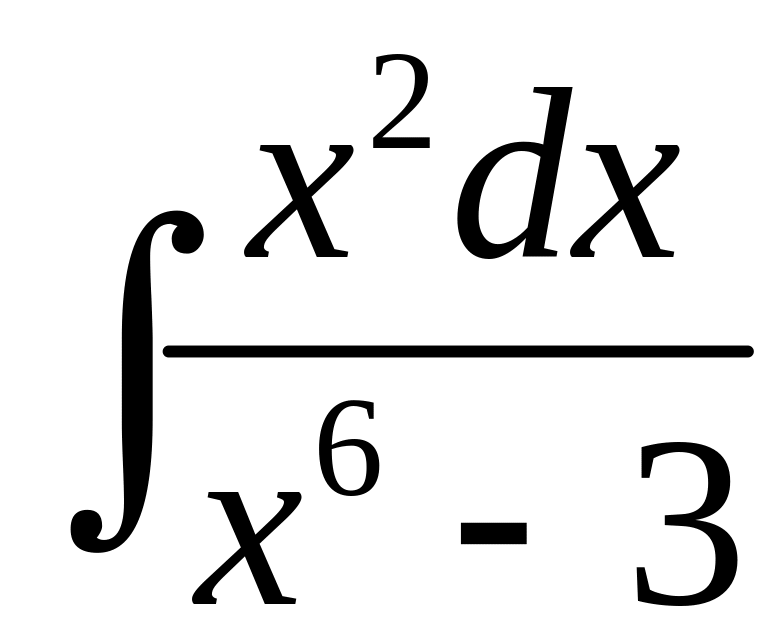 .
.
Решение.
а) В неопределенном интеграле
выполним замену
![]() ,
чтобы свести его к табличному виду.
Получим:
,
чтобы свести его к табличному виду.
Получим:
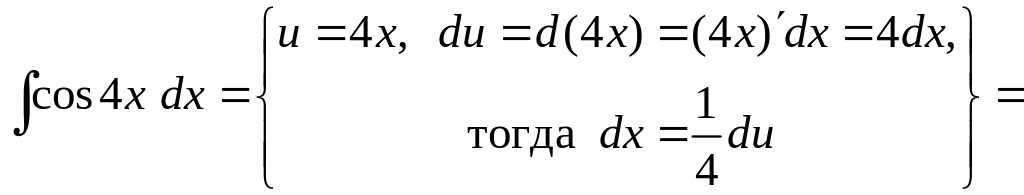
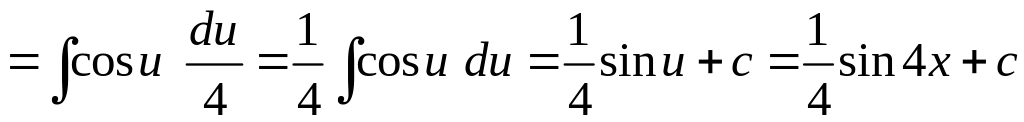 .
.
При вычислении неопределенного интеграла, полученного в результате замены, использовали табличную формулу 6 (см. раздел Справочный материал, Таблица интегралов).
б)
В неопределенном интеграле
выполним замену
![]() ,
чтобы свести его к табличному виду.
Получим:
,
чтобы свести его к табличному виду.
Получим:

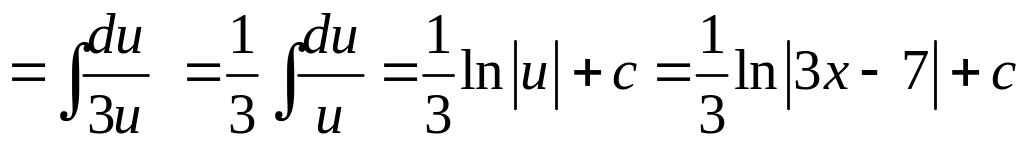 .
.
При вычислении неопределенного интеграла, полученного в результате замены, использовали табличную формулу 4 (см. раздел Справочный материал, Таблица интегралов).
в)
В неопределенном интеграле
выполним замену
![]() ,
чтобы свести его к табличному виду.
Получим:
,
чтобы свести его к табличному виду.
Получим:
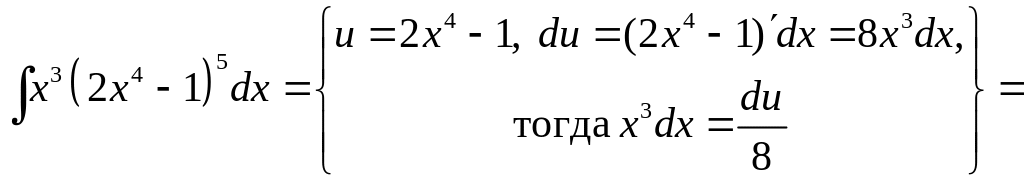
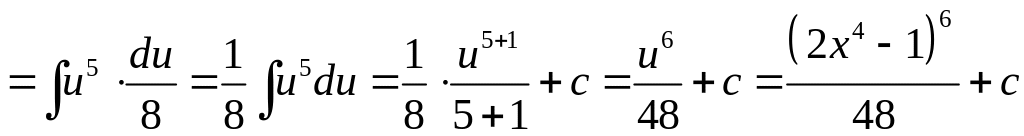 .
.
При вычислении неопределенного интеграла, полученного в результате замены, использовали табличную формулу 3 (см. раздел Справочный материал, Таблица интегралов).
г)
В неопределенном интеграле
выполним замену
![]() ,
чтобы свести его к табличному виду.
Получим:
,
чтобы свести его к табличному виду.
Получим:

![]() .
.
При вычислении неопределенного интеграла, полученного в результате замены, использовали табличную формулу 14 (см. раздел Справочный материал, Таблица интегралов).
д)
В неопределенном интеграле
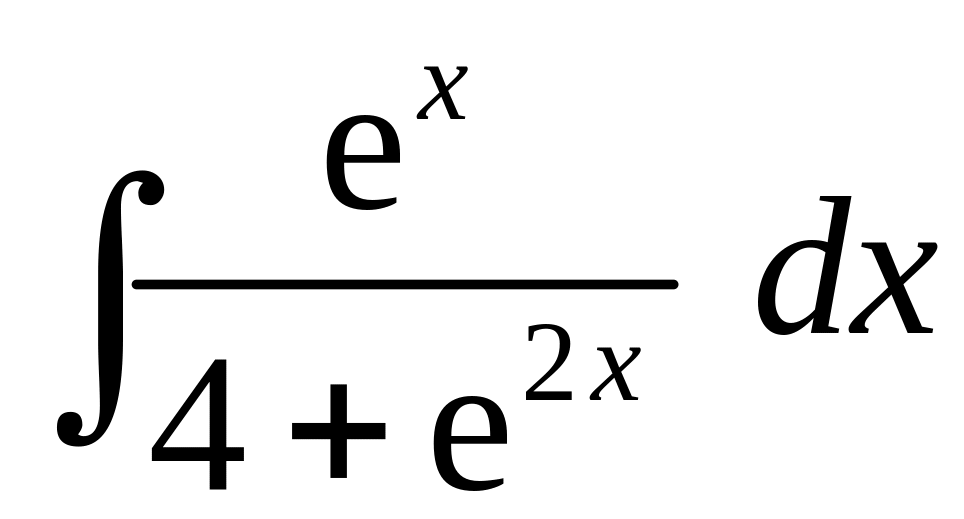 выполним замену
выполним замену
![]() для сведения его к табличному виду.
Получим:
для сведения его к табличному виду.
Получим:
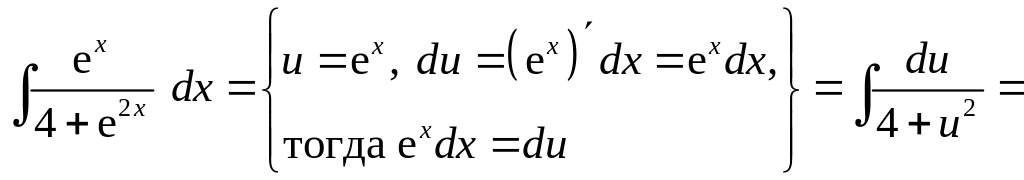
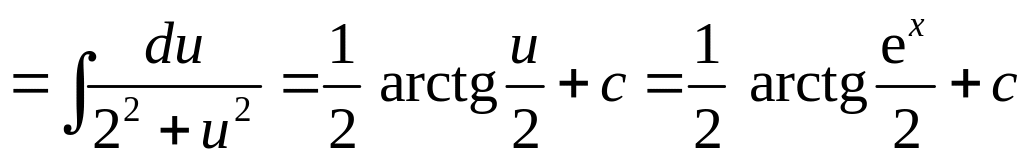 .
.
При вычислении неопределенного интеграла, полученного в результате замены, использовали табличную формулу 9 (см. раздел Справочный материал, Таблица интегралов).
е)
В неопределенном интеграле
сделаем замену
![]() для того, чтобы свести его к табличному
виду. Имеем:
для того, чтобы свести его к табличному
виду. Имеем:
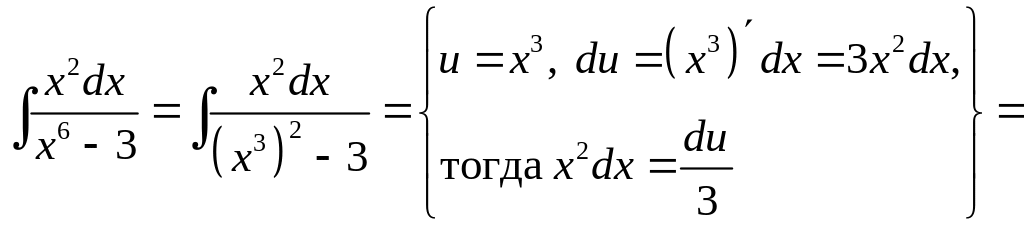

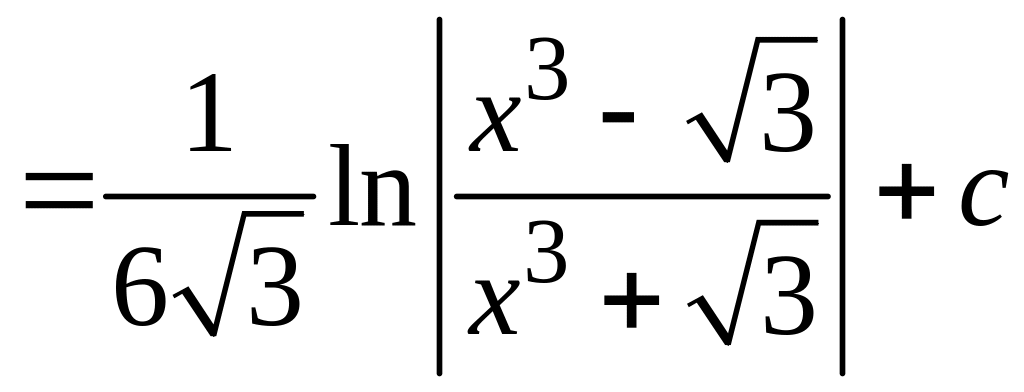 .
.
При вычислении неопределенного интеграла, полученного в результате замены, использовали табличную формулу 12 (см. раздел Справочный материал, Таблица интегралов).
Пример 25. Найти неопределенные интегралы методом интегрирования по частям:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
При решении задания будем использовать формулу интегрирования по частям в неопределенном интеграле:
![]() .
.
Решение.
а) Если под знаком неопределенного
интеграла стоит произведение алгебраической
функции на тригонометрическую или
показательную функцию, то при интегрировании
по частям за
![]() принимают алгебраическую функцию. В
данном примере под знаком интеграла
стоит произведение алгебраической
функции
принимают алгебраическую функцию. В
данном примере под знаком интеграла
стоит произведение алгебраической
функции
![]() и показательной функции
и показательной функции
![]() .
Примем за
алгебраическую функцию
.
Имеем:
.
Примем за
алгебраическую функцию
.
Имеем:
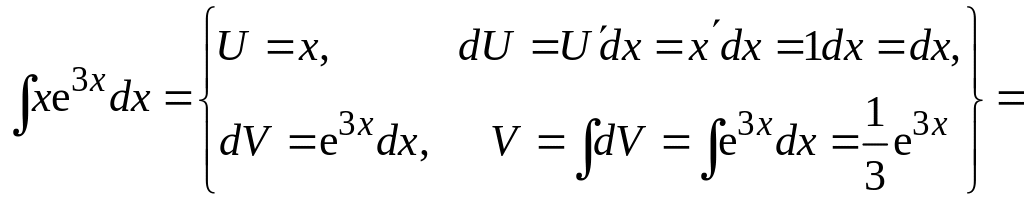

 .
.
При
вычислении функции
(см. рассуждения в фигурных скобках) не
добавляется произвольная постоянная,
т.к. в конечный результат эта постоянная
не входит. Это легко проверить подставив
в формулу интегрирования по частям
вместо
функцию
![]() .
.
б)
Если под знаком неопределенного интеграла
стоит произведение алгебраической
функции на тригонометрическую или
показательную функцию, то при интегрировании
по частям за
принимают алгебраическую функцию. В
данном примере под знаком интеграла
стоит произведение алгебраической
функции
![]() и тригонометрической функции
и тригонометрической функции
![]() .
Примем за
алгебраическую функцию
.
Имеем:
.
Примем за
алгебраическую функцию
.
Имеем:

![]() .
.
Интеграл
![]() снова вычислим по частям, приняв за
алгебраическую функцию
снова вычислим по частям, приняв за
алгебраическую функцию
![]() .
Получим:
.
Получим:

![]()
![]() .
.
Тогда исходный интеграл
![]()
![]() .
.
При вычислении функции (см. рассуждения в фигурных скобках) произвольная постоянная не добавляется.
в)
Если под знаком неопределенного интеграла
стоит произведение алгебраической
функции на обратную тригонометрическую
или логарифмическую функцию, то при
интегрировании по частям за
принимают обратную тригонометрическую
или логарифмическую функцию. В данном
примере под знаком интеграла стоит
произведение алгебраической функции
![]() и обратной тригонометрической функции
и обратной тригонометрической функции
![]() .
Примем за
алгебраическую функцию
.
Имеем:
.
Примем за
алгебраическую функцию
.
Имеем:

 .
.
Интеграл
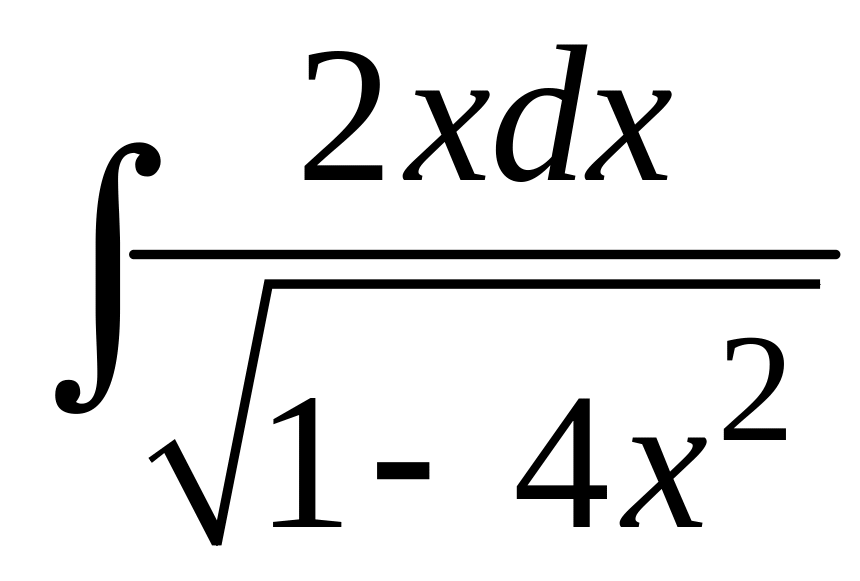 вычислим отдельно, используя метод
замены переменной. Имеем
вычислим отдельно, используя метод
замены переменной. Имеем
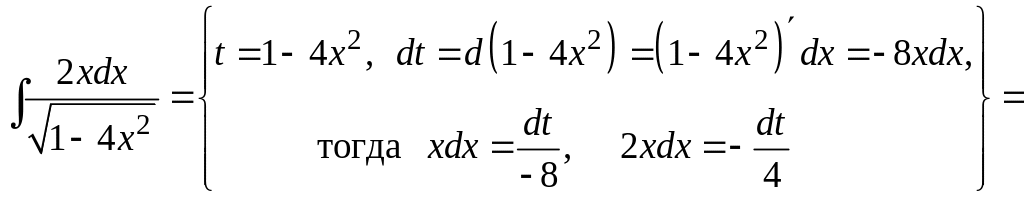
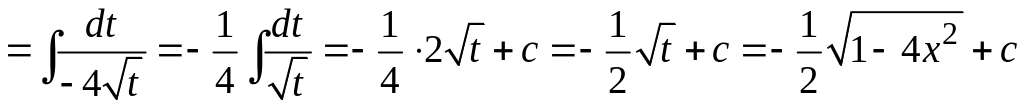 .
.
При
вычислении функции V
(см. рассуждения в фигурных скобках)
произвольная постоянная не добавляется.
При вычислении интеграла
![]() использовалась табличная формула 3
(см. раздел Справочный
материал,
Таблица
интегралов).
Окончательно получаем:
использовалась табличная формула 3
(см. раздел Справочный
материал,
Таблица
интегралов).
Окончательно получаем:
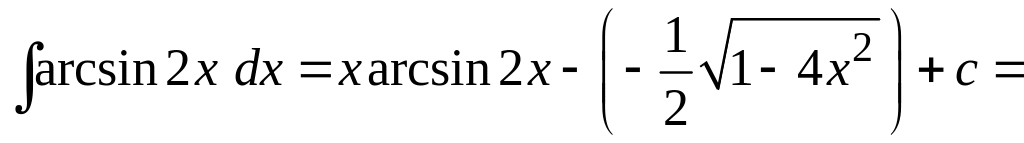
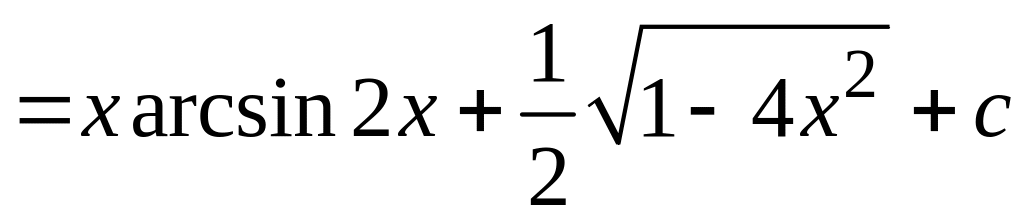 .
.
г)
Если под знаком неопределенного интеграла
стоит произведение алгебраической
функции на обратную тригонометрическую
или логарифмическую функцию, то при
интегрировании по частям за
принимают обратную тригонометрическую
или логарифмическую функцию. В данном
примере под знаком интеграла стоит
произведение алгебраической функции
![]() и логарифмической функции
и логарифмической функции
![]() .
Примем за
алгебраическую функцию
.
Имеем:
.
Примем за
алгебраическую функцию
.
Имеем:


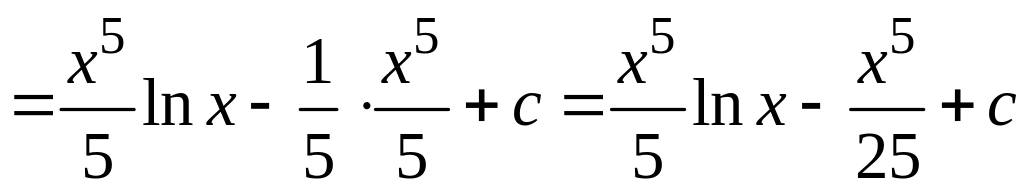 .
.
При
вычислении функции
(см. рассуждения в фигурных скобках)
произвольная постоянная не добавляется.
При вычислении интеграла
![]() использовалась табличная формула 3 (см.
раздел Справочный
материал,
Таблица
интегралов).
использовалась табличная формула 3 (см.
раздел Справочный
материал,
Таблица
интегралов).
Пример 26. Найти неопределенные интегралы от рациональных дробей:
а)
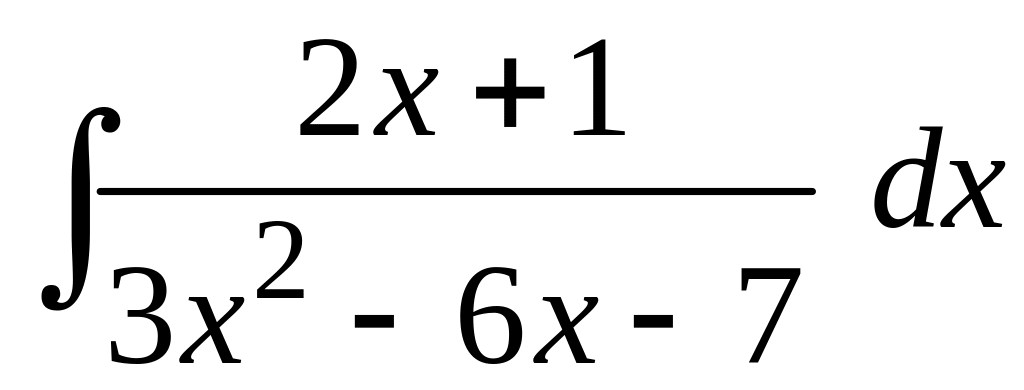 ;
б)
;
б)
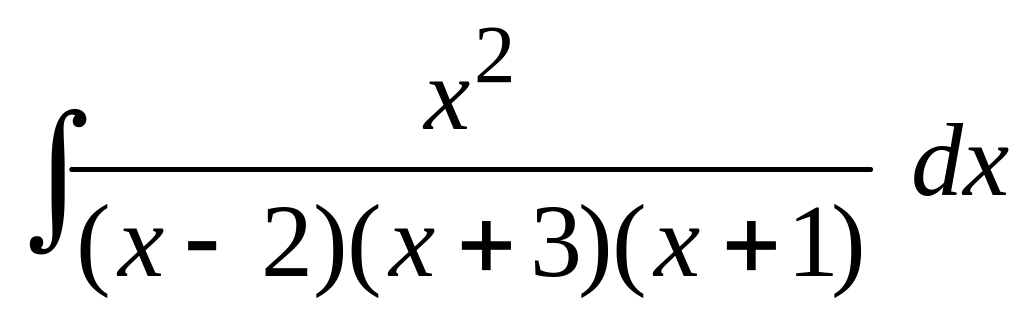 ;
;
в)
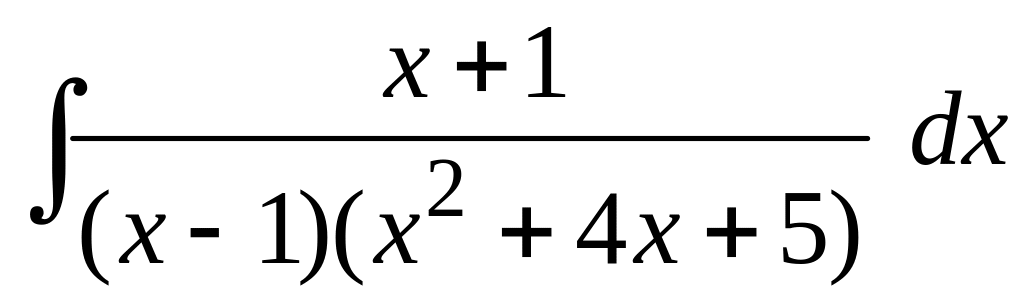 .
.
Решение.
а) Под знаком неопределенного интеграла
стоит рациональная дробь, в числителе
которой многочлен первой степени, в
знаменателе – второй степени. Для
вычисления интеграла от такой дроби в
числитель записывают производную
знаменателя и уравнивают новый числитель
со старым. Интеграл разбивают на сумму
двух интегралов: выражение под знаком
первого содержит в числителе производную
знаменателя дроби. Второй получившийся
интеграл вычисляют путем выделения в
знаменателе полного квадрата. Производная
знаменателя
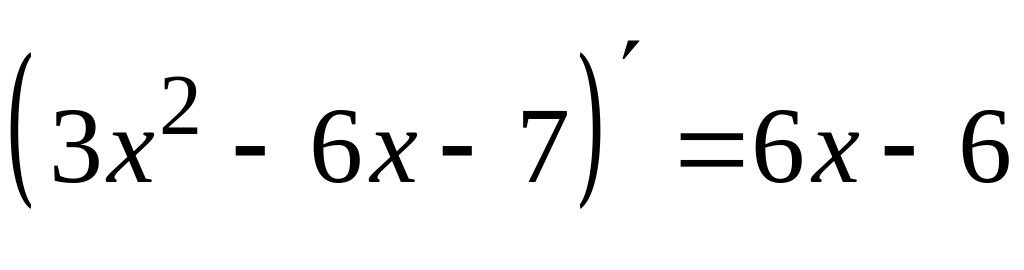 .
Тогда
.
Тогда
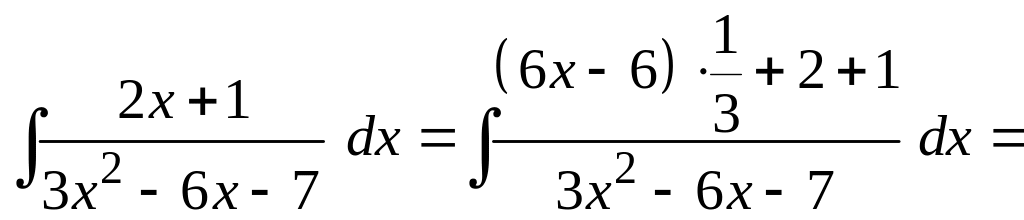
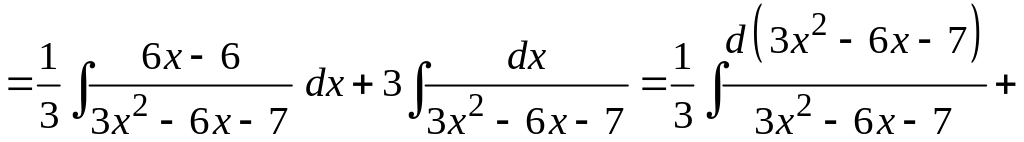
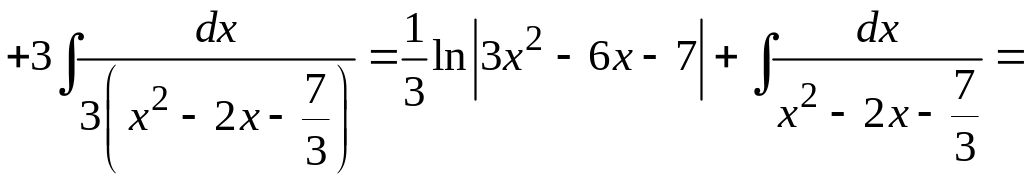

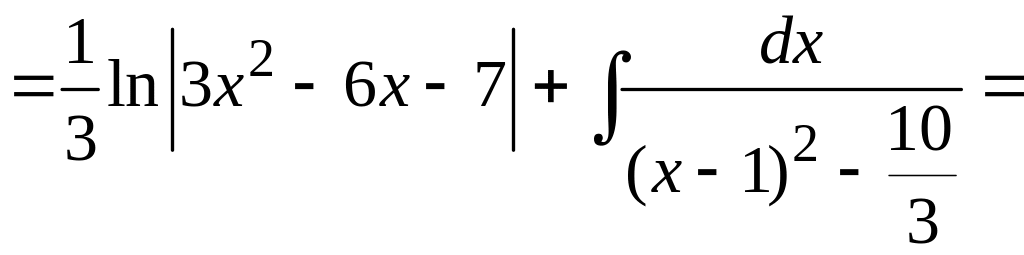
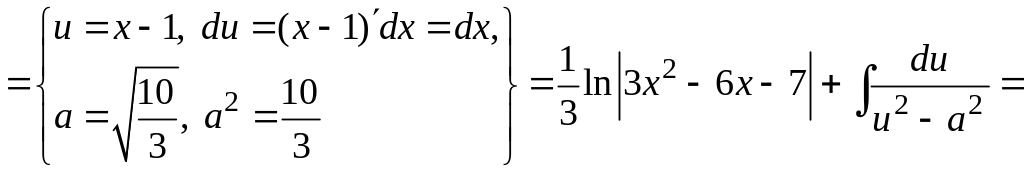
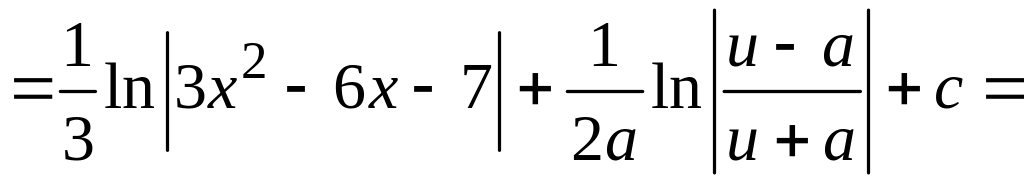
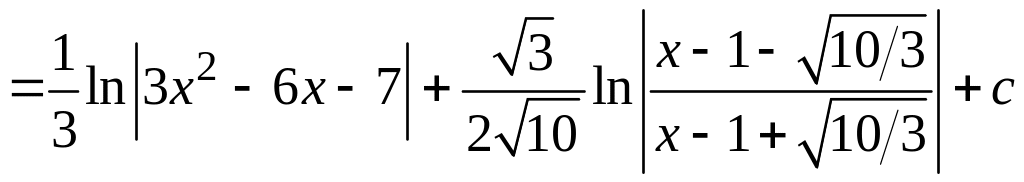 .
.
При вычислении неопределенного интеграла, полученного в результате замены, использовали табличную формулу 12 (см. раздел Справочный материал, Таблица интегралов).
б) Под знаком неопределенного интеграла стоит рациональная дробь, в числителе которой многочлен второй степени, в знаменателе – третьей степени. Знаменатель разложен на множители. Разобьем дробь, стоящую под знаком интеграла, на сумму простейших дробей:
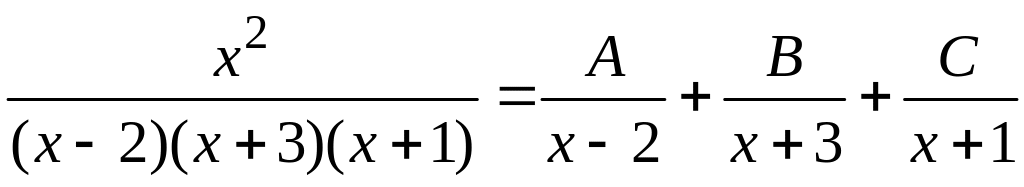 .
.
Приведем сумму простейших дробей к общему знаменателю и приравняем коэффициенты при одинаковых степенях в старом и новом числителях. Имеем:
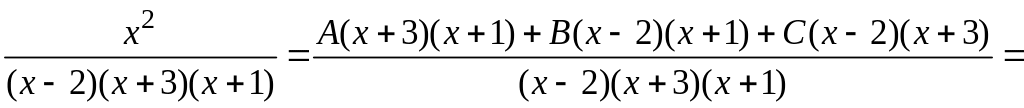
 ,
,
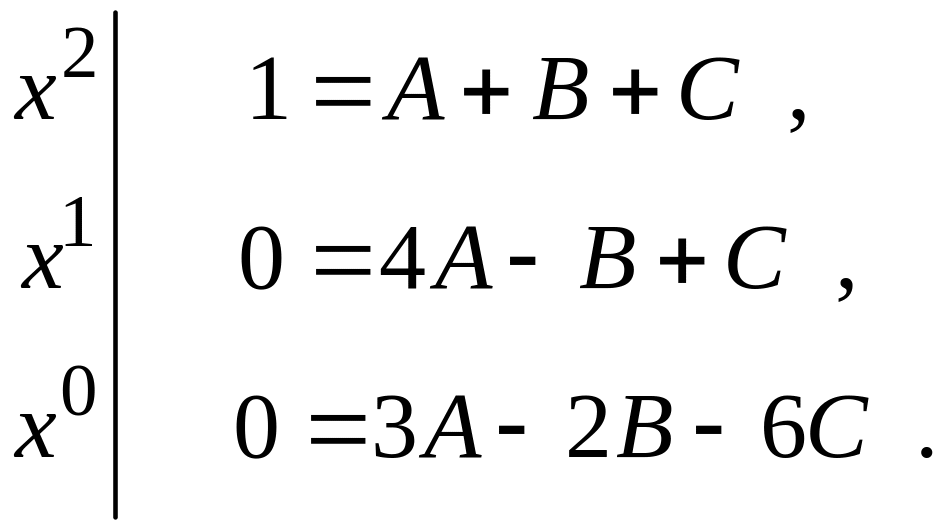
Получили систему трех уравнений с тремя неизвестными. Сложим первое уравнение системы со вторым. Имеем
![]() .
(*)
.
(*)
Второе уравнение системы умножим на 2 и вычтем из него третье уравнение. Получим:
![]() .
(**)
.
(**)
Из
равенств (*) и (**) находим
![]() ,
,
![]() .
Подставив найденные значения
и
в первое уравнение системы, находим
.
Подставив найденные значения
и
в первое уравнение системы, находим
![]() .
С учетом найденных коэффициентов
исходный интеграл можно представить в
виде суммы трех интегралов:
.
С учетом найденных коэффициентов
исходный интеграл можно представить в
виде суммы трех интегралов:

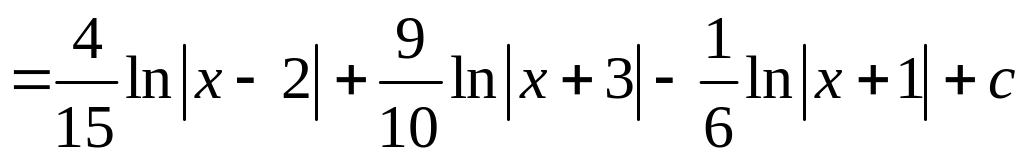 .
.
в) Под
знаком неопределенного интеграла
стоит рациональная дробь, в числителе
которой многочлен первой степени, в
знаменателе – третьей степени. Знаменатель
разложен на множители (квадратный
трехчлен на множители не раскладывается,
т.к. дискриминант
![]() ).
Разобьем дробь, стоящую под знаком
интеграла, на сумму простейших дробей:
).
Разобьем дробь, стоящую под знаком
интеграла, на сумму простейших дробей:
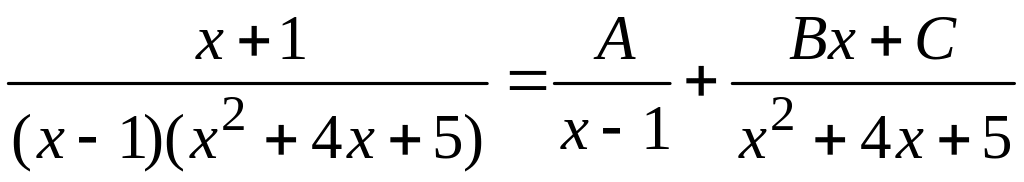 .
.
Приведем сумму простейших дробей к общему знаменателю и приравняем коэффициенты при одинаковых степенях в старом и новом числителях. Имеем:

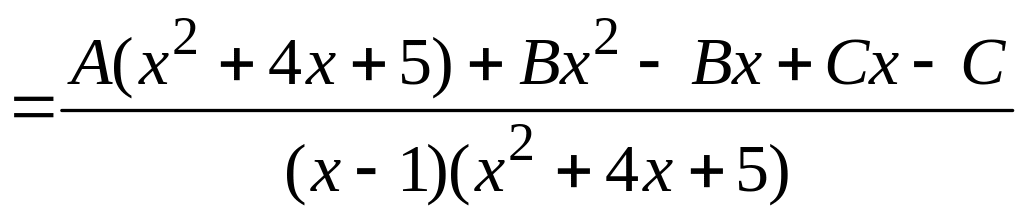 ,
,
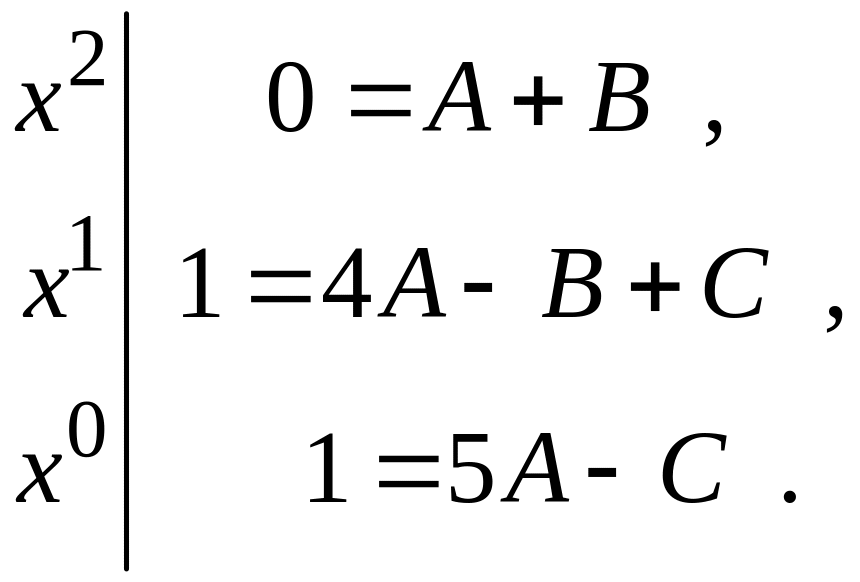
Из
первого уравнения системы находим
![]() ,
из третьего уравнения системы находим
,
из третьего уравнения системы находим
![]() .
Подставим найденные значения во второе
уравнение системы. Имеем:
.
Подставим найденные значения во второе
уравнение системы. Имеем:
![]() ,
,
 .
.
Тогда
![]() ,
,
![]() .
С учетом
найденных коэффициентов исходный
интеграл можно представить в виде суммы
двух интегралов:
.
С учетом
найденных коэффициентов исходный
интеграл можно представить в виде суммы
двух интегралов:
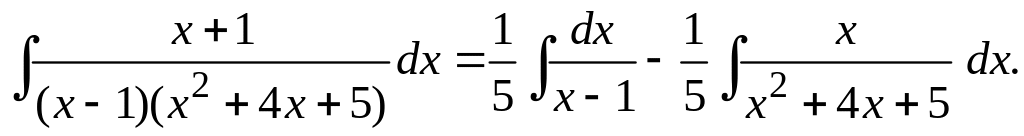
Последний интеграл в предыдущем равенстве вычислим аналогично тому, как это было сделано выше в данном примере под пунктом а). Имеем:
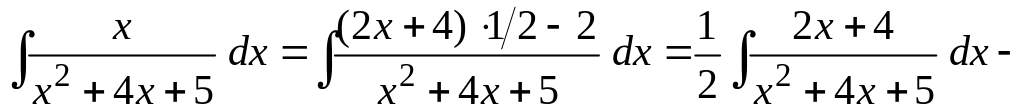
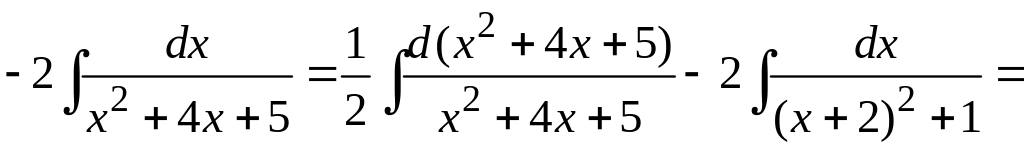
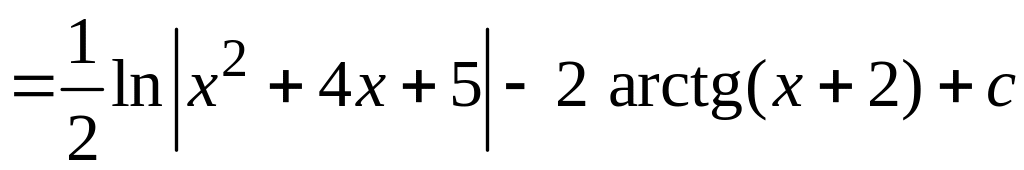 .
.
При вычислении неопределенных интегралов, полученных в результате преобразований, использовались табличные формулы 4 и 9 (см. раздел Справочный материал, Таблица интегралов). Имеем для исходного интеграла
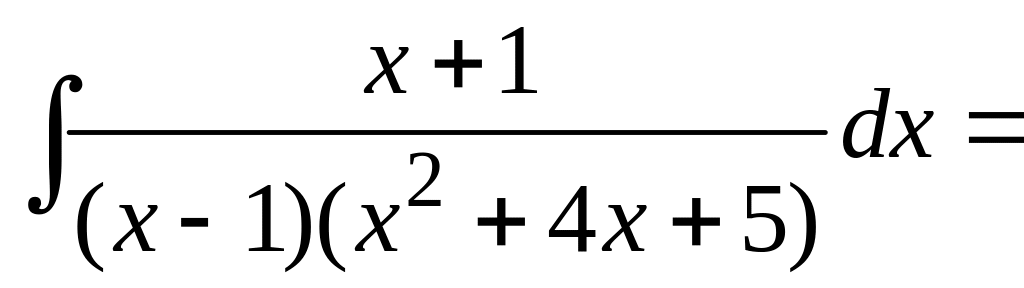
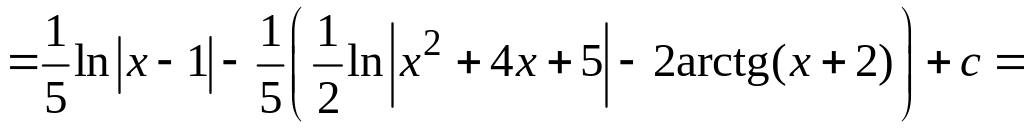
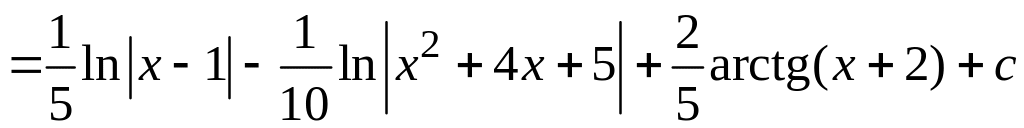 .
.
Пример 27. Найти неопределенные интегралы от тригонометрических выражений:
а)
![]() ;
б)
;
б)
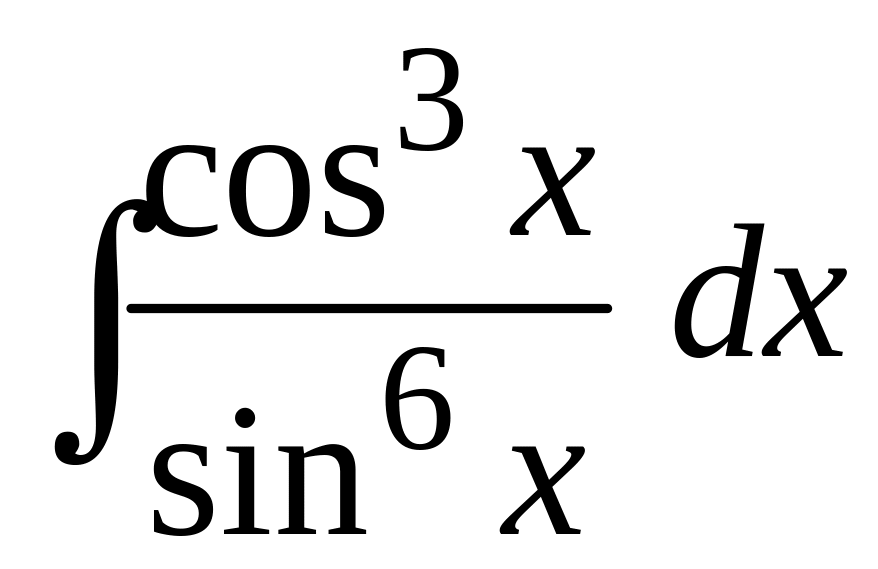 ;
в)
;
в)
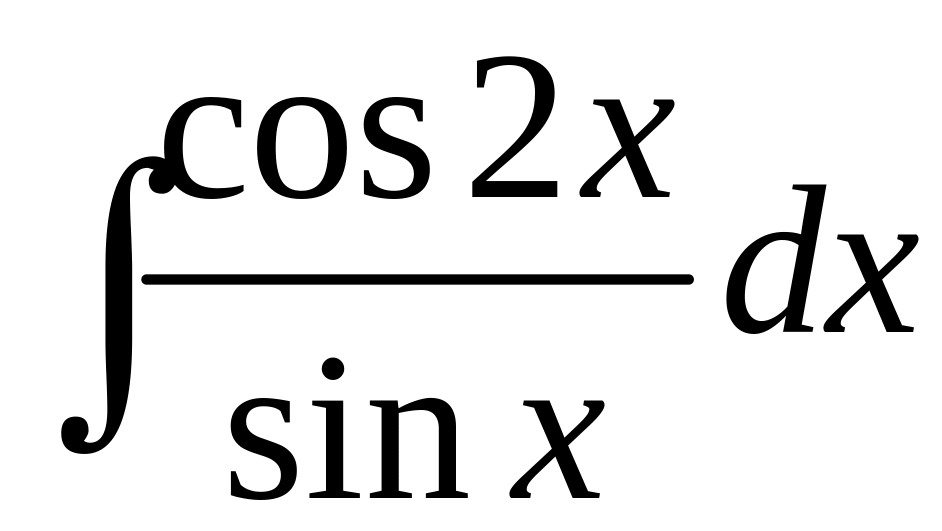 .
.
Решение. а) Вычислим неопределенный интеграл , используя следующую связь между тригонометрическими функциями:
![]() ,
,
![]()
(см. раздел Справочный материал, Основные тригонометрические формулы; Правила дифференцирования, Таблица производных). Получим
![]()
![]()
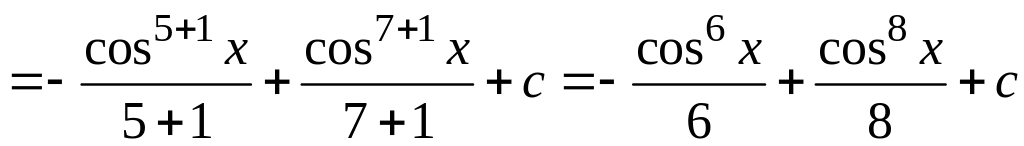 .
.
При вычислении неопределенных интегралов, полученных в результате преобразований, использовалась табличная формула 3 (см. раздел Справочный материал, Таблица интегралов).
б) Вычислим неопределенный интеграл , используя следующую связь между тригонометрическими функциями:
![]() ,
,
![]()
(см. раздел Справочный материал, Основные тригонометрические формулы; Правила дифференцирования, Таблица производных). Получим

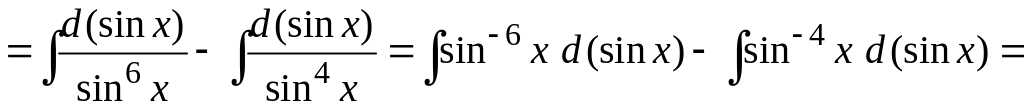
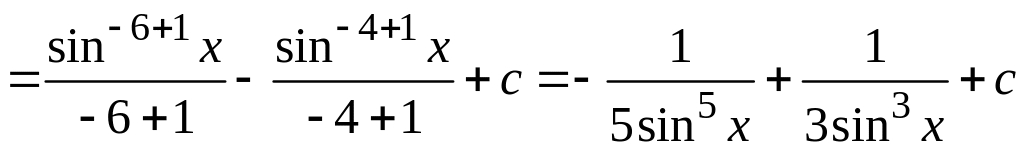 .
.
При вычислении неопределенных интегралов, полученных в результате преобразований, использовалась табличная формула 3 (см. раздел Справочный материал, Таблица интегралов).
в) Вычислим неопределенный интеграл , используя следующую тригонометрическую формулу для косинуса двойного угла:
![]()
(см. раздел Справочный материал, Основные тригонометрические формулы). Получим
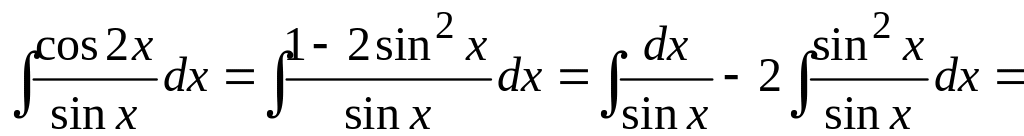
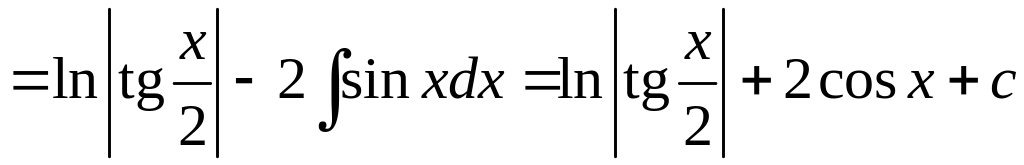 .
.
При вычислении неопределенных интегралов, полученных в результате преобразований, использовалась табличные формулы 7 и 16 (см. раздел Справочный материал, Таблица интегралов).
Пример
28. Найти
площадь фигуры, ограниченной параболой
![]() и прямой
и прямой
![]() .
.
Решение.
Построим на чертеже фигуру, площадь
которой нужно найти. Абсцисса вершины
параболы
находится по формуле
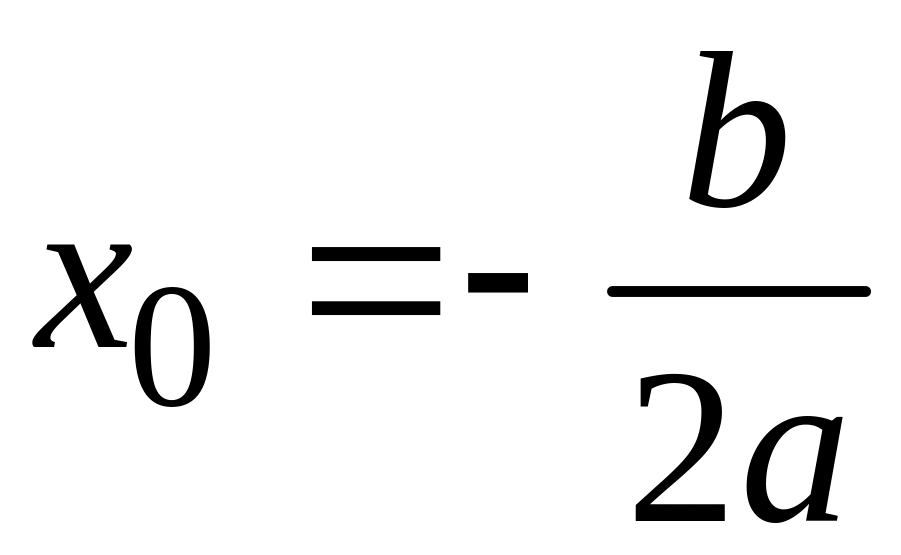 .
В нашем случае
.
В нашем случае
![]() ,
,
![]() и
и
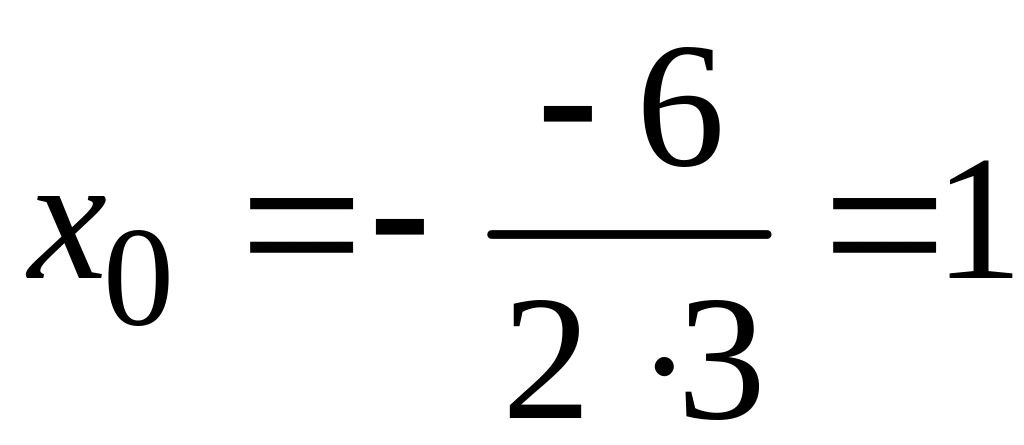 ,
,
![]() ,
,
т.е.
координаты вершины параболы
![]() .
Найдем точки пересечения параболы и
прямой. Для этого решим систему
.
Найдем точки пересечения параболы и
прямой. Для этого решим систему
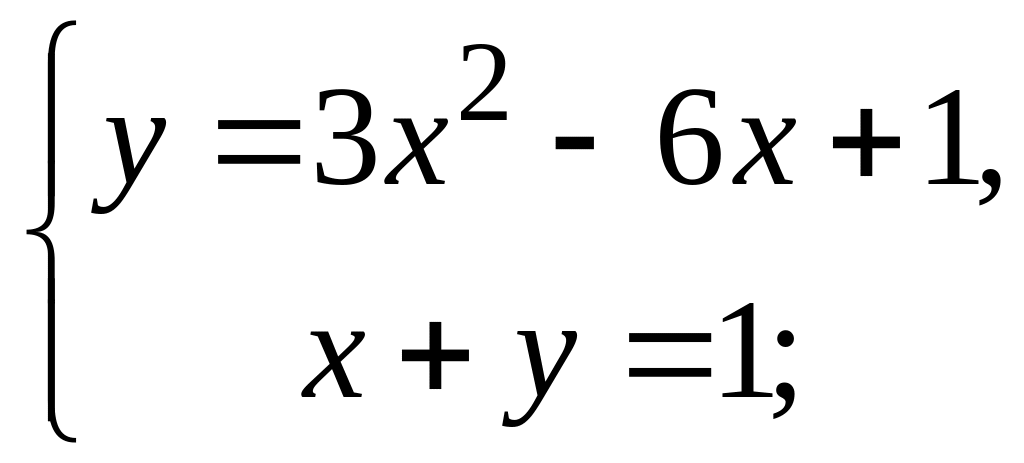
![]()
![]()
![]() .
.
Решая
последнее уравнение, находим
![]() ,
,
![]() .
Тогда точки пересечения имеют координаты
и
.
Тогда точки пересечения имеют координаты
и
![]() .
.
С
учетом вычислений выполним построение
фигуры. Эта фигура ограничена сверху
прямой
,
снизу параболой
,
с боков – прямыми
и
![]() (см. рис. 16). Площадь фигуры вычислим по
формуле:
(см. рис. 16). Площадь фигуры вычислим по
формуле:
,
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() (см. раздел
Справочный
материал,
Геометрические
приложения определенного интеграла).
Получим
(см. раздел
Справочный
материал,
Геометрические
приложения определенного интеграла).
Получим


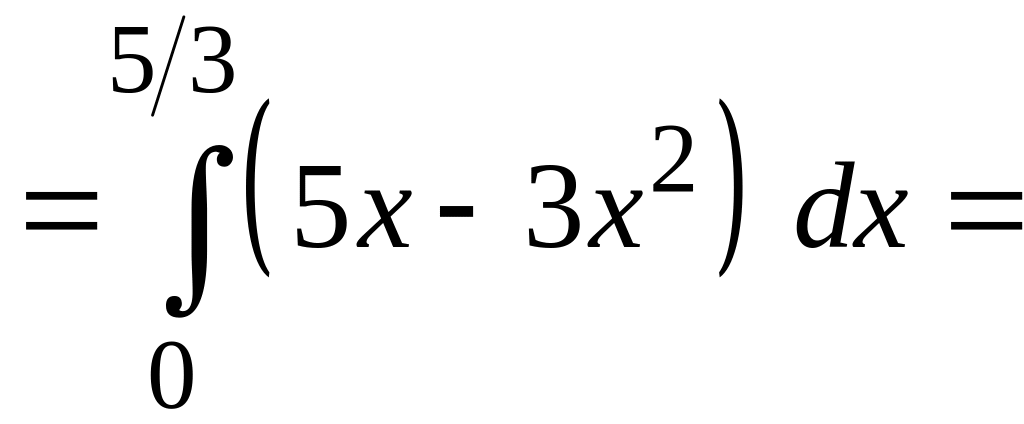
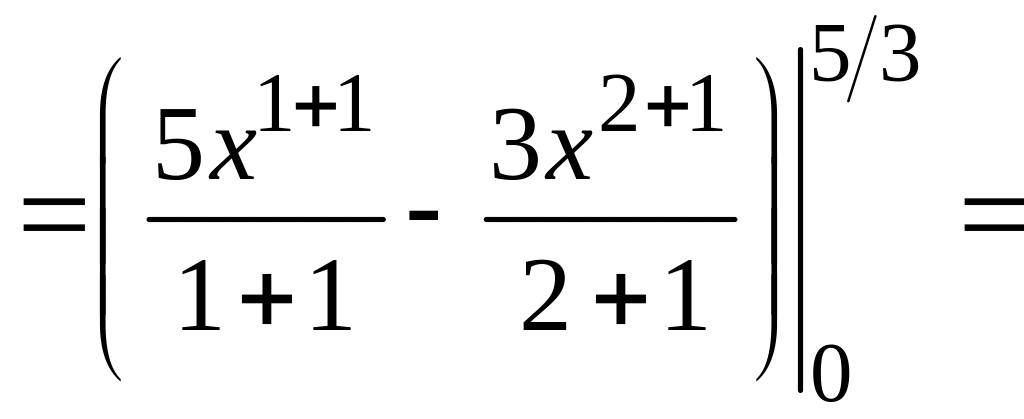
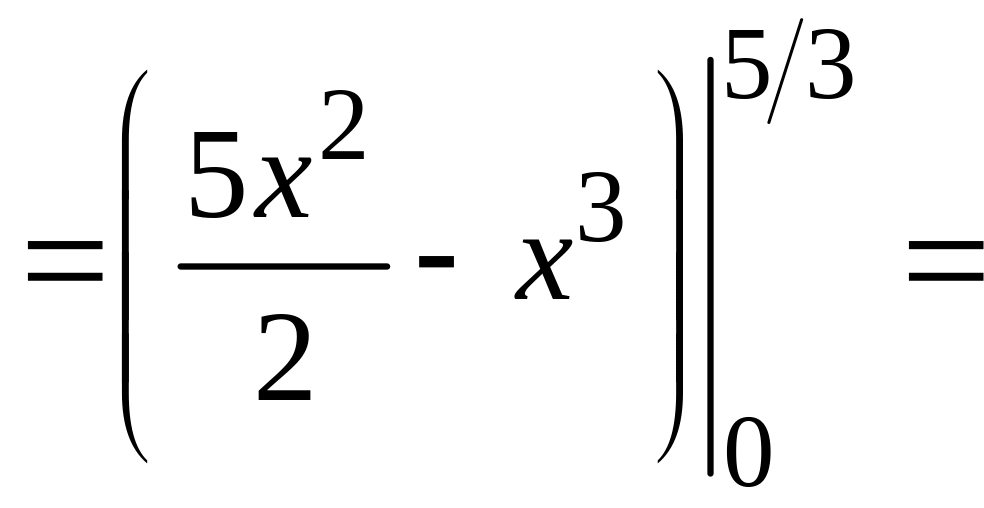
Р
и с. 16
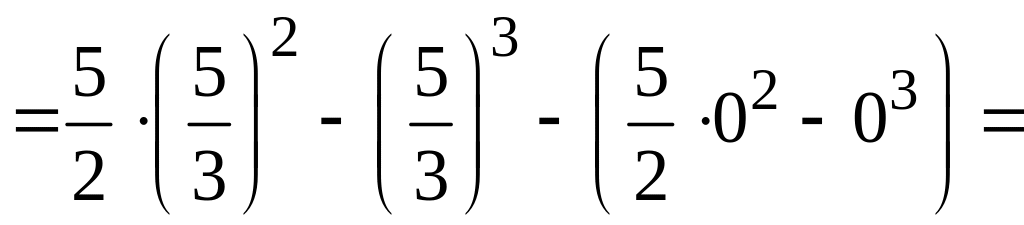
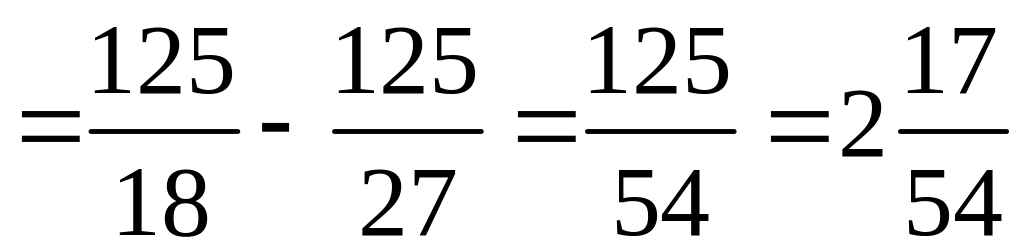 (кв.
ед).
(кв.
ед).
Пример
29. Найти
площадь фигуры, ограниченной параболами
![]() и
и
![]() .
.
Решение.
Построим на
чертеже фигуру, площадь которой нужно
найти. Абсцисса вершины параболы
находится по формуле
.
В нашем случае
![]() ,
,
![]() и
и
 ,
,
![]() ,
,
т.е.
координаты вершины параболы
![]() .
Абсцисса вершины параболы
находится по формуле
.
В нашем примере
.
Абсцисса вершины параболы
находится по формуле
.
В нашем примере
![]() ,
,
![]() .
Имеем:
.
Имеем:
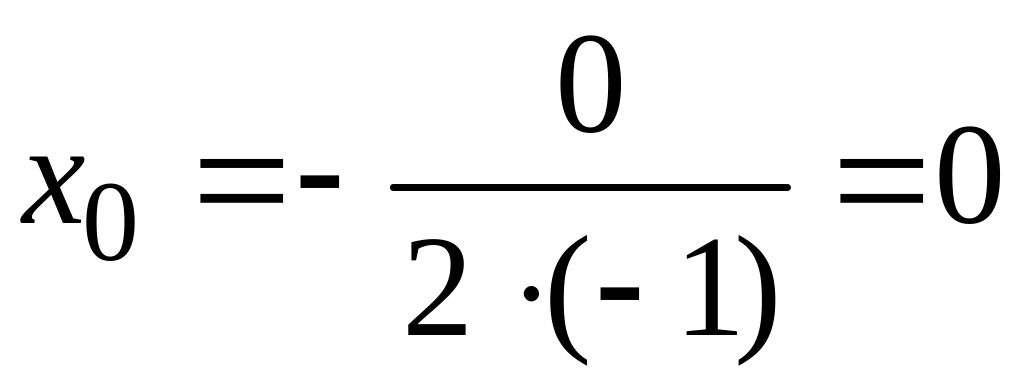 ,
,
![]() ,
,
т.е.
координаты вершины параболы
![]() .
Найдем точки пересечения парабол. Для
этого решим систему
.
Найдем точки пересечения парабол. Для
этого решим систему
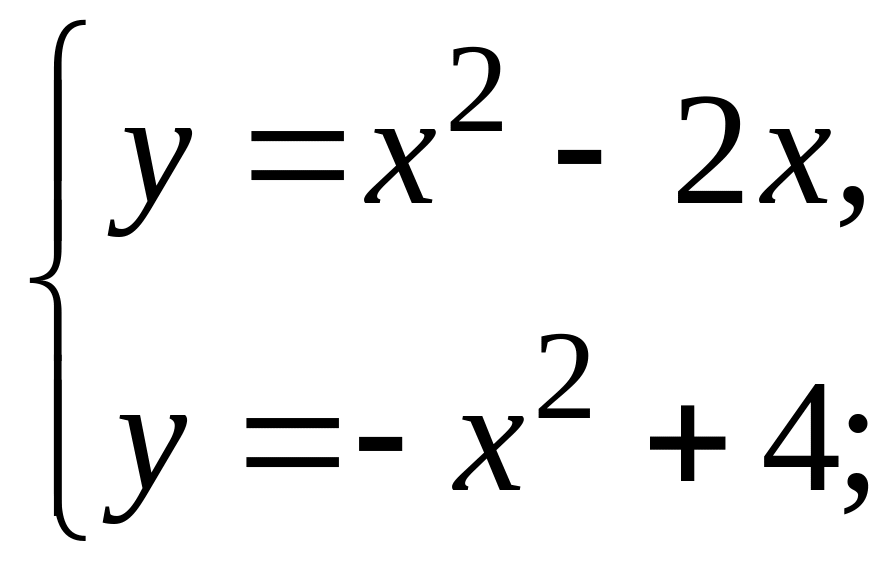
![]()
![]() .
.
Р ешая
последнее уравнение, находим
ешая
последнее уравнение, находим
![]() ,
,
![]() .
Тогда точки пересечения имеют координаты
.
Тогда точки пересечения имеют координаты
![]() и
и
![]() .
.
С
учетом вычислений выполним построение
фигуры. Эта фигура ограничена сверху
параболой
,
снизу параболой
,
с боков – прямыми
![]() и
(см. рис. 17). Площадь фигуры вычислим по
формуле:
и
(см. рис. 17). Площадь фигуры вычислим по
формуле:
,
Р
и с. 17
где
,
,
![]() ,
,
![]() (см.
раздел Справочный
материал,
Геометрические
приложения определенного интеграла).
Получим
(см.
раздел Справочный
материал,
Геометрические
приложения определенного интеграла).
Получим
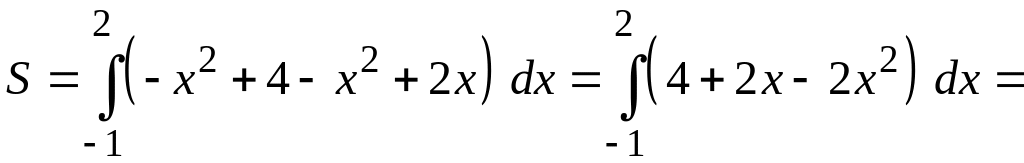

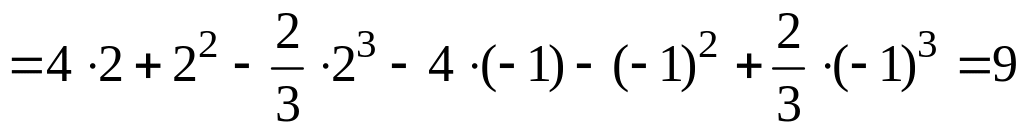 (кв.ед.).
(кв.ед.).
Пример
30. Вычислить
площадь фигуры, ограниченной параболой
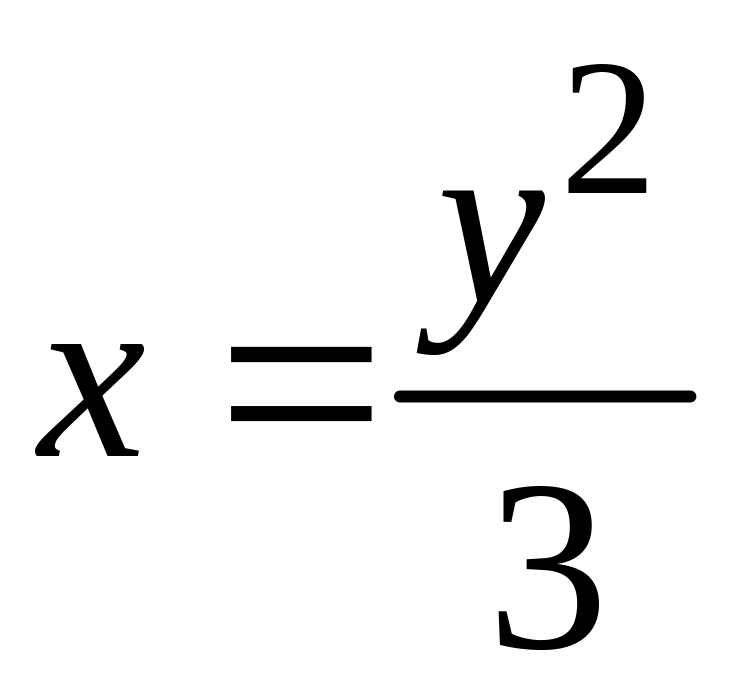 и прямой
.
и прямой
.
Решение. Выполним построение фигуры, площадь которой требуется найти. Ветви параболы направлены вправо вдоль оси , вершина находится в начале координат. Найдем точки пересечения параболы с прямой . Для этого решим систему
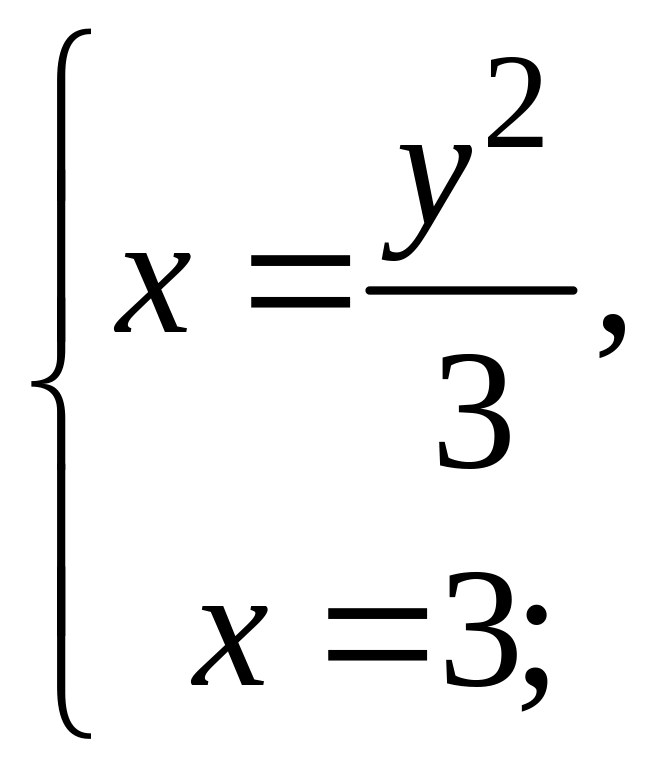
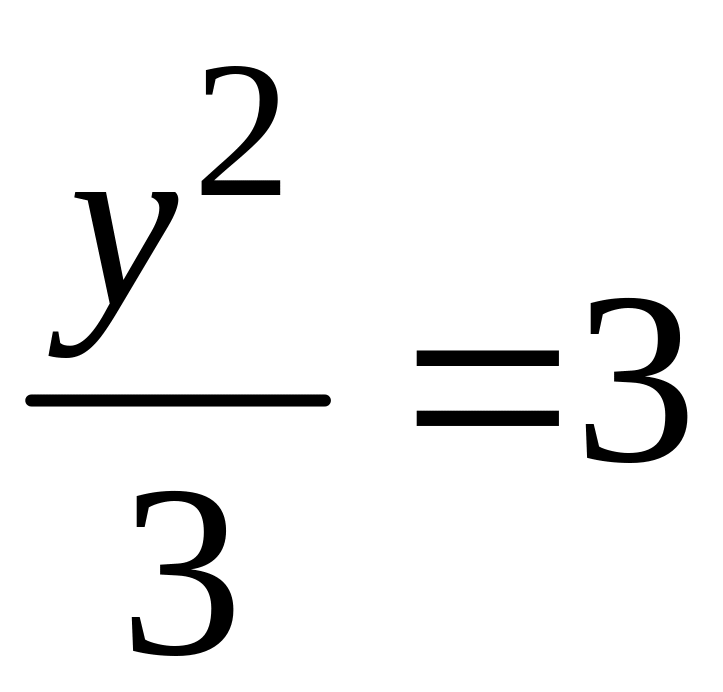
![]() .
.
Решая
последнее уравнение, находим
![]() ,
,
![]() .
Тогда точки пересечения имеют координаты
.
Тогда точки пересечения имеют координаты
![]() и
и
![]() .
С учетом вычислений выполним построение
фигуры. Эта фигура ограничена слева
параболой
.
С учетом вычислений выполним построение
фигуры. Эта фигура ограничена слева
параболой
![]() ,
справа прямой
,
снизу и сверху – прямыми
и
,
справа прямой
,
снизу и сверху – прямыми
и
![]() (см. рис. 18). Площадь фигуры вычислим по
формуле:
(см. рис. 18). Площадь фигуры вычислим по
формуле:
,
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() (см. раздел
Справочный
материал,
Геометрические
приложения определенного интеграла).
Получим
(см. раздел
Справочный
материал,
Геометрические
приложения определенного интеграла).
Получим


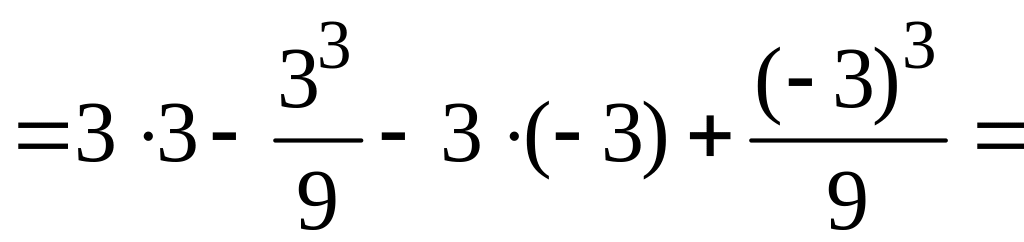
![]() (кв.
ед.)
(кв.
ед.)
Р и с. 18
Пример
31. Найти
координаты центра тяжести однородной
плоской фигуры, ограниченной параболой
![]() и прямой
и прямой
![]() .
.
Решение.
Построим фигуру, координаты центра
тяжести которой нужно найти. Абсцисса
вершины параболы
находится по формуле
,
где
![]() ,
.
Имеем:
,
.
Имеем:
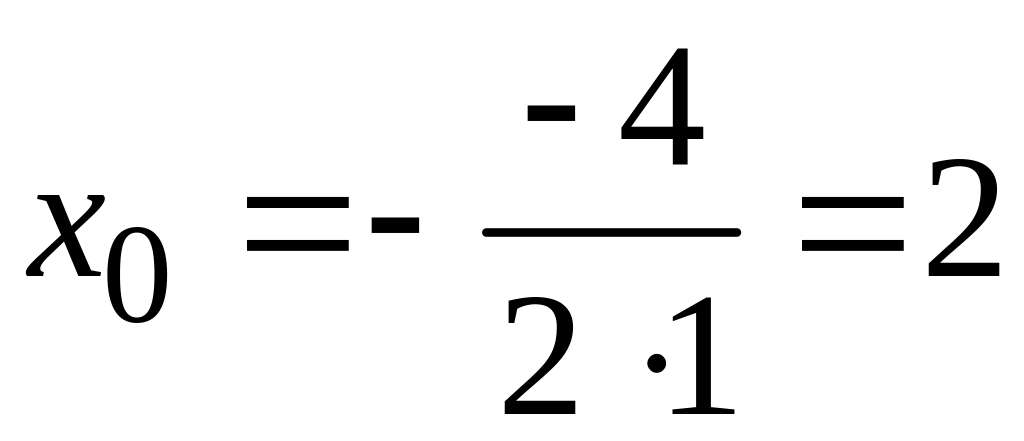 ,
,
![]() ,
,
т.е.
координаты вершины параболы
![]() .
Найдем точки пересечения параболы и
прямой
.
Для этого решим систему
.
Найдем точки пересечения параболы и
прямой
.
Для этого решим систему

![]()
![]() .
.
Решая
последнее уравнение, находим
,
![]() .
Тогда точки пересечения имеют координаты
.
Тогда точки пересечения имеют координаты
![]() и
и
![]() .
С учетом вычислений выполним построение
фигуры. Эта фигура ограничена снизу
параболой
,
сверху прямой
.
С учетом вычислений выполним построение
фигуры. Эта фигура ограничена снизу
параболой
,
сверху прямой
![]() ,
слева и справа – прямыми
и
(см. рис. 19). Координаты центра тяжести
плоской однородной фигуры находятся
по формулам:
,
слева и справа – прямыми
и
(см. рис. 19). Координаты центра тяжести
плоской однородной фигуры находятся
по формулам:
 ,
,
,
,
Р и с. 19
где
,
![]() ,
,
![]() ,
,
![]() (см. раздел
Справочный
материал,
Геометрические
приложения определенного интеграла).
Получим
(см. раздел
Справочный
материал,
Геометрические
приложения определенного интеграла).
Получим
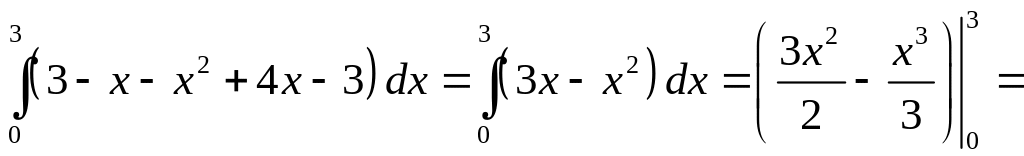
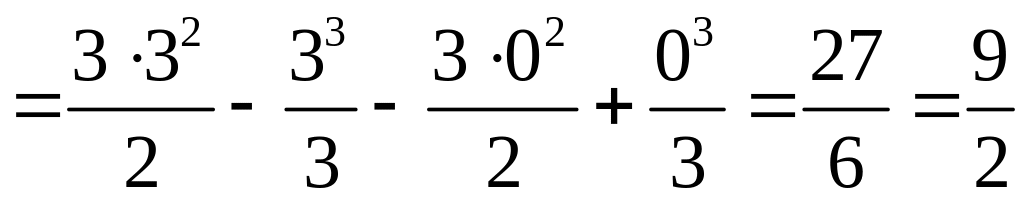 ;
;
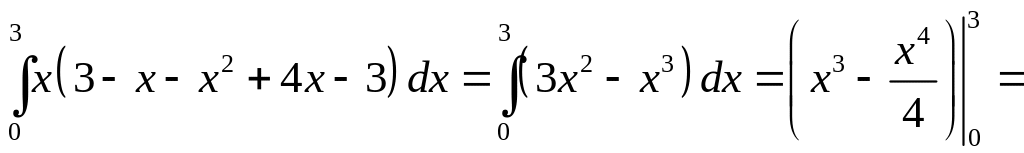
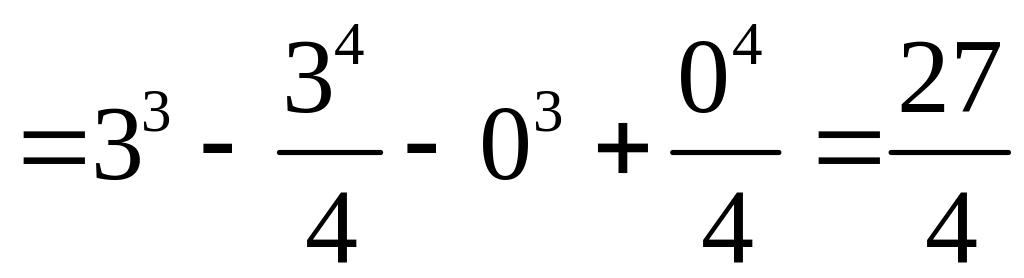 ;
;
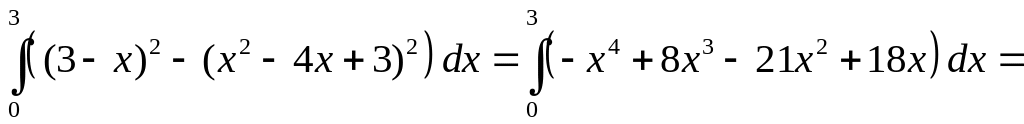

 .
.
Тогда
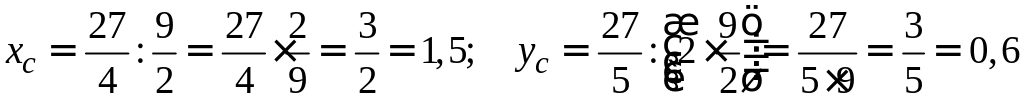 .
.
Итак, центр тяжести данной фигуры имеет координаты (1,5; 0,6).
Пример
32. Найти
объем тела, полученного при вращении
вокруг оси
фигуры, ограниченной кривой
![]() и прямыми
,
и прямыми
,
![]() .
.
Р ешение.
Выполним на чертеже фигуру, которая
вращается вокруг оси
.
Эта фигура ограничена сверху кривой
ешение.
Выполним на чертеже фигуру, которая
вращается вокруг оси
.
Эта фигура ограничена сверху кривой
![]() ,
снизу прямой
,
с боков – прямыми
и
(см. рис. 20). Объем тела, полученного при
вращении фигуры вокруг оси
,
вычислим по формуле:
,
снизу прямой
,
с боков – прямыми
и
(см. рис. 20). Объем тела, полученного при
вращении фигуры вокруг оси
,
вычислим по формуле:
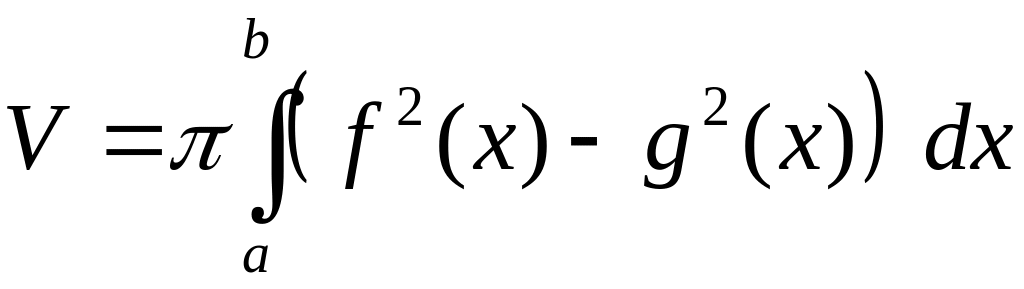 ,
,
где
,
,
![]() ,
,
![]() (см. раздел
Справочный
материал,
Геометрические
приложения определенного интеграла).
Получим
(см. раздел
Справочный
материал,
Геометрические
приложения определенного интеграла).
Получим
Р и с. 20
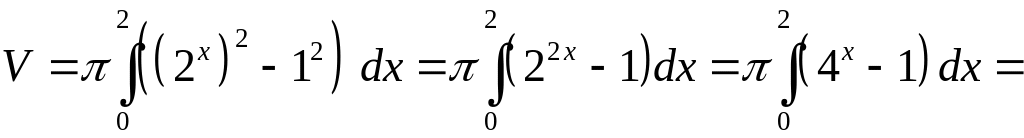

 (куб.
ед.).
(куб.
ед.).
Пример 33. Найти объем тела, полученного при вращении вокруг оси фигуры, ограниченной гиперболой , осью и прямыми , .
Решение.
Построим на чертеже фигуру, которая
вращается вокруг оси
.
Эта фигура ограничена сверху прямой
,
снизу прямой
,
слева осью
(
),
справа кривой
![]() (см. рис. 21). Объем тела, полученного при
вращении фигуры вокруг оси
,
вычислим по формуле:
(см. рис. 21). Объем тела, полученного при
вращении фигуры вокруг оси
,
вычислим по формуле:
,
г де
де
![]() ,
,
,
,
![]() ,
,
![]() (см. раздел
Справочный
материал,
Геометрические
приложения определенного интеграла).
(см. раздел
Справочный
материал,
Геометрические
приложения определенного интеграла).
Получим
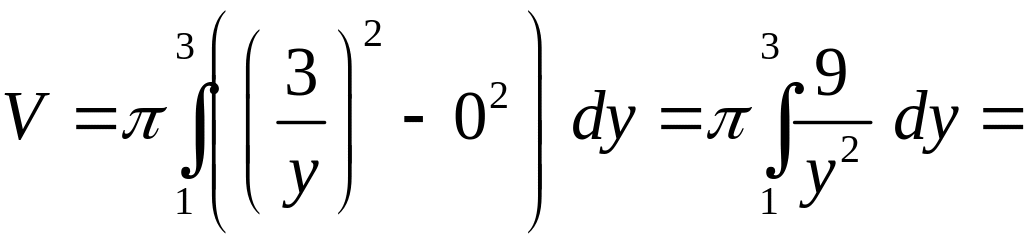
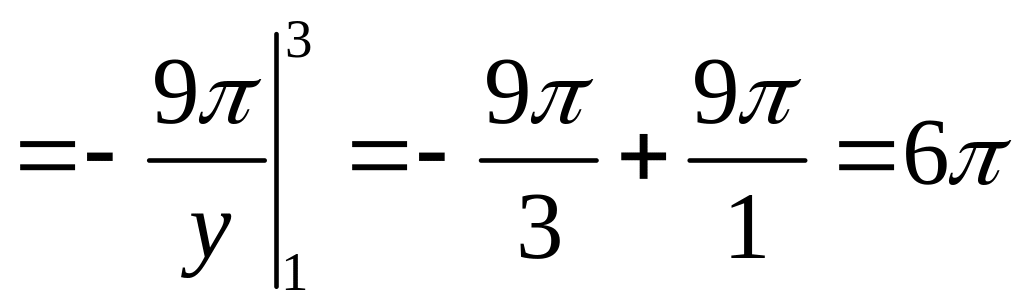 (куб.
ед.).
(куб.
ед.).
Р и с. 21
