
- •Кафедра высшей математики
- •Порядок выполнения контрольных работ
- •Рекомендуемая литература
- •Справочный материал
- •Указания к выполнению контрольной работы 1
- •Примеры решения задач
- •Контрольная работа 1
- •Указания к выполнению контрольной работы 2
- •Примеры решения задач
- •Контрольная работа 2
- •Указания к выполнению контрольной работы 3
- •Примеры решения задач
- •Контрольная работа 3
- •Указания к выполнению контрольной работы 4
- •Примеры решения задач
- •Контрольная работа 4
- •Содержание
- •Ответственный за выпуск м.Г. Плотников Корректор г.Н. Елисеева
Указания к выполнению контрольной работы 1
Т е м а 1. Элементы аналитической геометрии
на плоскости
ЛИТЕРАТУРА:
[5], гл. 1–6;
[6], гл. I, § 1–4, упр. 1, 5, 13; гл. III, § 1–4, § 6–7, упр. 1, 5–8, 11, 18;
[7], задачи 3, 28, 63, 64, 82, 87, 95, 99.
Т е м а 2. Основы векторной алгебры
ЛИТЕРАТУРА:
[5], гл. 7–10;
[6], гл. XVIII, упр. 1, 5;
[7], задачи 372, 373, 376, 380, 383, 386, 390, 394, 399, 400, 402, 418, 426, 427, 434, 438, 439, 444.
Т е м а 3. Элементы аналитической геометрии
в пространстве
ЛИТЕРАТУРА:
[5], гл. 11–13;
[6], гл. XIX, § 1–4, упр. 2;
[7], задачи 474, 475.
Т е м а 4. Системы линейных уравнений
ЛИТЕРАТУРА:
[6], гл. XVII, § 7, упр. 9, 11;
[7], задачи 624, 625, 627.
Примеры решения задач
Пример
1. Даны
координаты вершин треугольника АВС:
![]() ,
,
![]() ,
,
![]() .
Найти: 1) уравнения сторон треугольника
АВС
и угловые коэффициенты этих сторон; 2)
угол
.
Найти: 1) уравнения сторон треугольника
АВС
и угловые коэффициенты этих сторон; 2)
угол
![]() треугольника АВС;
3) уравнение медианы
треугольника АВС;
3) уравнение медианы
![]() ;
4) уравнение высоты
;
4) уравнение высоты
![]() и координаты точки
и координаты точки
![]() ;
5) уравнение прямой
;
5) уравнение прямой
![]() ,
проходящей через вершину
,
проходящей через вершину
![]() параллельно стороне
параллельно стороне
![]() ;
6) построить на координатной плоскости
треугольник
;
6) построить на координатной плоскости
треугольник
![]() ,
медиану
,
высоту
и прямую
.
,
медиану
,
высоту
и прямую
.
Решение.
1) Уравнение прямой, проходящей через
точки с координатами
![]() и
и
![]() на плоскости, имеет вид
на плоскости, имеет вид
 .
(1)
.
(1)
Подставляя
в равенство (1) координаты точек
![]() и
,
получаем уравнение стороны
и
,
получаем уравнение стороны
![]() :
:
 ;
;
 ;
;
 ;
;
![]() ;
;
![]() ;
;
![]() (общее
уравнение стороны
).
(общее
уравнение стороны
).
Выразив
![]() из общего уравнения стороны
,
находим угловой коэффициент прямой
:
из общего уравнения стороны
,
находим угловой коэффициент прямой
:
![]() ;
;
 ,
откуда
,
откуда
 .
.
Подставляя
в равенство (1) координаты точек
и
,
получаем уравнение стороны
![]() :
:
 ;
;
 ;
;
 ;
;
![]() ;
;
![]() ;
;
![]() (общее
уравнение стороны
).
(общее
уравнение стороны
).
Выразив из общего уравнения стороны , находим угловой коэффициент прямой :
![]() ,
откуда
,
откуда
![]() .
.
Подставляя в равенство (1) координаты точек и , получаем уравнение стороны :
 ;
;
 ;
;
 ;
;
![]() ;
;
![]() ;
;
![]() (общее
уравнение стороны
).
(общее
уравнение стороны
).
Выразив из общего уравнения стороны , находим угловой коэффициент прямой :
 ,
откуда
,
откуда
 .
.
2)
Тангенс угла
![]() между двумя прямыми с угловыми
коэффициентами
между двумя прямыми с угловыми
коэффициентами
![]() и
и
![]() вычисляется по формуле:
вычисляется по формуле:
. (2)
Угол треугольника АВС заключен между прямыми и , угловые коэффициенты которых найдены выше и равны и соответственно. Подставим значения угловых коэффициентов в формулу (2) и найдем:
 .
.
Из
последнего равенства следует, что
тангенс угла
треугольника не существует. По таблице
2, приведенной
в разделе Справочный
материал,
определяем, что
![]() .
.
3)
Чтобы найти уравнение медианы
,
определим сначала координаты точки
![]() ,
которая является серединой отрезка
,
применяя формулы для координат середины
отрезка:
,
которая является серединой отрезка
,
применяя формулы для координат середины
отрезка:
(3)
Подставляя
в формулы (3) координаты точек
![]() и
и
![]() ,
находим:
,
находим:
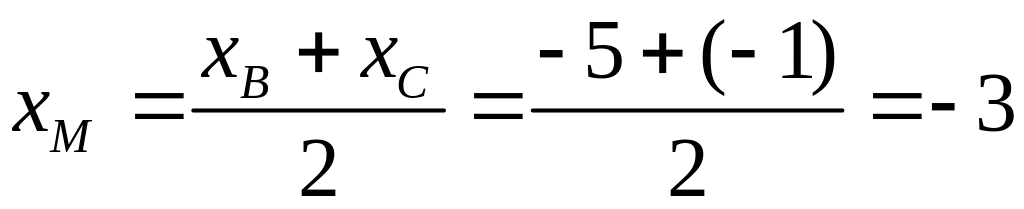 ;
;
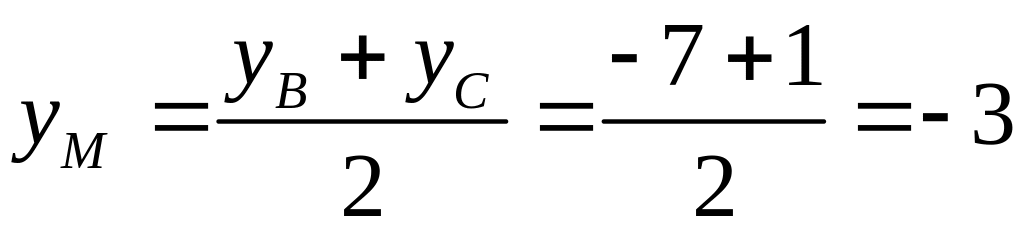 ;
;
![]() .
.
Подставим
в (1) координаты точек
![]() и
и
![]() и
найдем уравнение медианы
:
и
найдем уравнение медианы
:
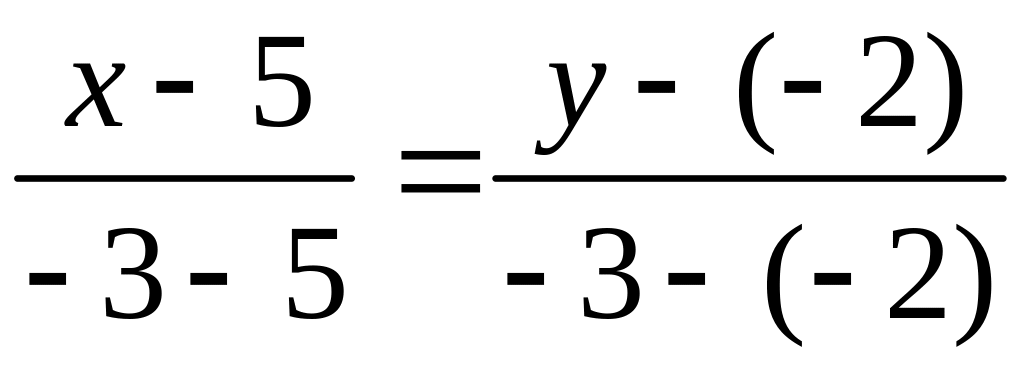 ;
;
![]()
 ;
;
 ;
;
![]() ;
;
![]() ;
;
![]() (общее
уравнение медианы
(общее
уравнение медианы
![]() ).
).
4) Уравнение прямой с известным угловым коэффициентом , проходящей через заданную точку , имеет вид
. (4)
Высота
![]() перпендикулярна стороне
перпендикулярна стороне
![]() .
Угловые коэффициенты взаимно
перпендикулярных прямых в произведении
дают
,
т.е.
.
Угловые коэффициенты взаимно
перпендикулярных прямых в произведении
дают
,
т.е.
![]() ,
откуда
,
откуда
 .
.
Подставим
координаты точки
и найденный угловой коэффициент
![]() в равенство (4). Получим
в равенство (4). Получим
![]() ;
;
![]() ;
;
![]() (общее
уравнение высоты
).
(общее
уравнение высоты
).
Найдем
координаты точки
![]() .
Эта точка является точкой пересечения
прямых
и
.
Поэтому координаты точки
можно найти, решив систему, составленную
из общих уравнений прямых
и
.
Решив систему
.
Эта точка является точкой пересечения
прямых
и
.
Поэтому координаты точки
можно найти, решив систему, составленную
из общих уравнений прямых
и
.
Решив систему
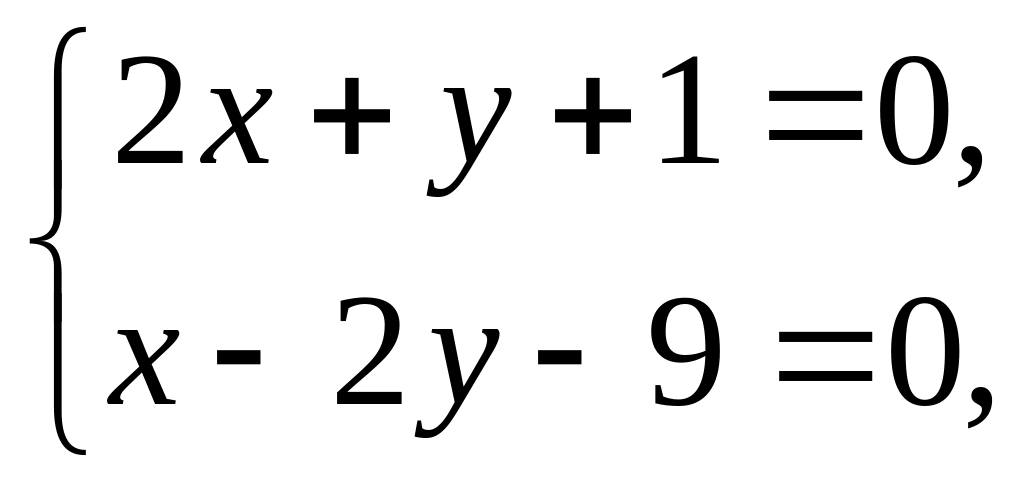
находим
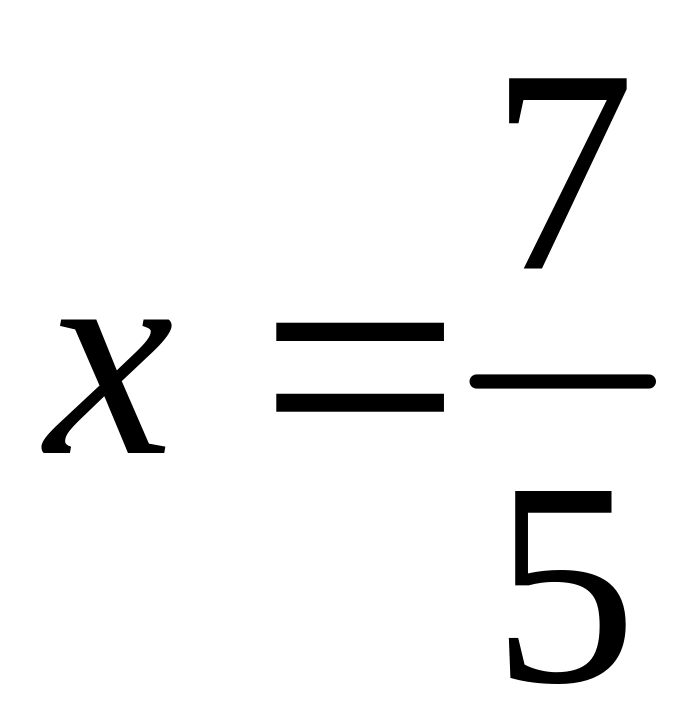 ,
,
 ,
т.е.
,
т.е.
![]() .
.
5)
Так как прямая
![]() параллельна стороне
параллельна стороне
![]() ,
то угловой коэффициент прямой
будет равен угловому коэффициенту
прямой
.
Подставив в (4) координаты вершины
и угловой коэффициент
,
то угловой коэффициент прямой
будет равен угловому коэффициенту
прямой
.
Подставив в (4) координаты вершины
и угловой коэффициент
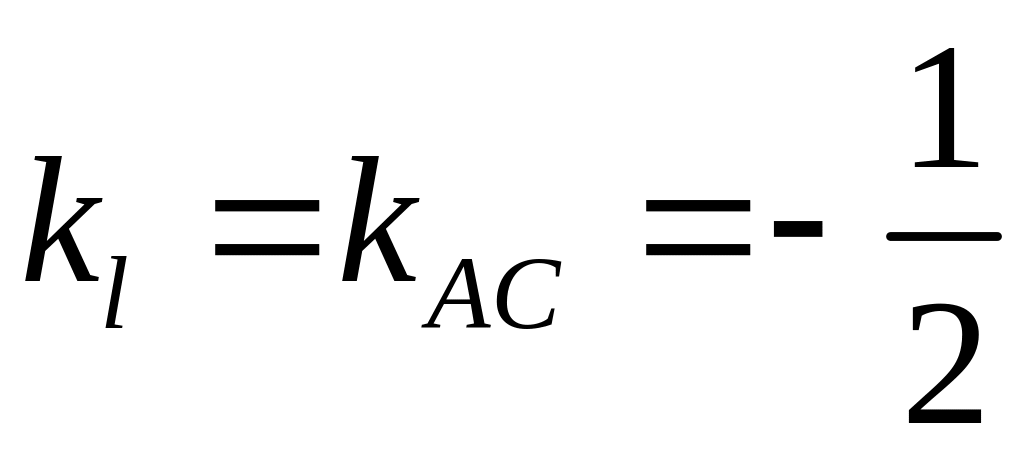 ,
получим
,
получим
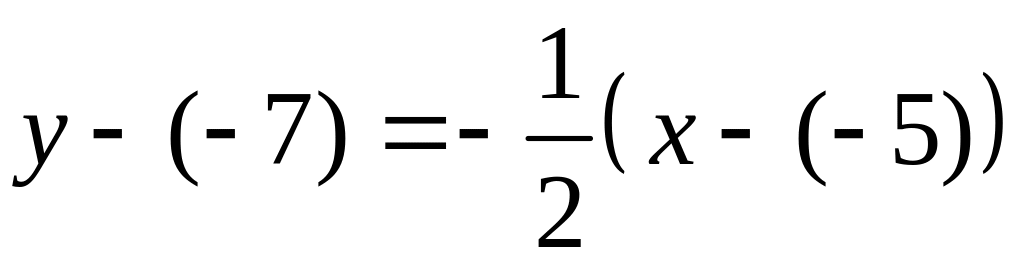 ;
;
![]() ;
;
![]() (общее
уравнение прямой
).
(общее
уравнение прямой
).
6) Построим на координатной плоскости (см. рис. 5) треугольник , медиану , высоту и прямую .

Р и с. 5
Пример
2. Даны
координаты вершин треугольника
:
![]() ,
,
![]() ,
,
![]() .
Построить на чертеже треугольник
и следующие
векторы: 1)
.
Построить на чертеже треугольник
и следующие
векторы: 1)
![]() и
и
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5)
![]() ;
6)
;
6)
![]() .
Найти: 7) длины сторон треугольника
.
Найти: 7) длины сторон треугольника
![]() ;
8) углы
и
треугольника
(в радианах с точностью
;
8) углы
и
треугольника
(в радианах с точностью
![]() ).
).
Решение.

1) В декартовой системе координат на плоскости по заданным координатам построим точки , и , соединим их отрезками.
Получим
треугольник
.
Векторы
![]() и
и
![]() построим, указав направление на отрезках
и
(см. рис. 6).
построим, указав направление на отрезках
и
(см. рис. 6).
Р и с. 6

2)
3) Вектор
![]() направлен также как и вектор
и больше его по длине в 2 раза. На рис. 7
вектор
направлен также как и вектор
и больше его по длине в 2 раза. На рис. 7
вектор
![]() .
Для построения вектора
.
Для построения вектора
![]() продолжим отрезок
.
На рис.7 вектор
продолжим отрезок
.
На рис.7 вектор
![]() .
.
Р и с. 7
4)
Вектор
![]() направлен в сторону, противоположную
вектору
направлен в сторону, противоположную
вектору
![]() ,
и больше его по длине в 3 раза. На рис. 8
вектор
,
и больше его по длине в 3 раза. На рис. 8
вектор
![]() .
.

Р и с. 8
5)
6) Чтобы построить векторы
![]() и
и
![]() ,
достроим треугольник
,
достроим треугольник
![]() до параллелограмма
до параллелограмма
![]() .
Диагонали построенного параллелограмма
с выбранным направлением будут искомыми
векторами:
.
Диагонали построенного параллелограмма
с выбранным направлением будут искомыми
векторами:
![]() и
и
![]() на рис. 9.
на рис. 9.

Р и с. 9
7) Расстояние между точками на плоскости с координатами и находится по формуле
![]() .
(5)
.
(5)
Подставляя в формулу (5) координаты вершин треугольника , находим длины сторон:
![]() ,
,
![]() ,
,
![]() .
.
8) Найдем углы и треугольника , используя следующую формулу:
 ,
(6)
,
(6)
где – угол между векторами и . Найдем координаты векторов , и их модули:
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Тогда по формуле (6) получаем

![]()
 (радиан).
(радиан).
Найдем
координаты векторов
![]() ,
,
![]() и их модули:
и их модули:
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Тогда по формуле (6) получаем
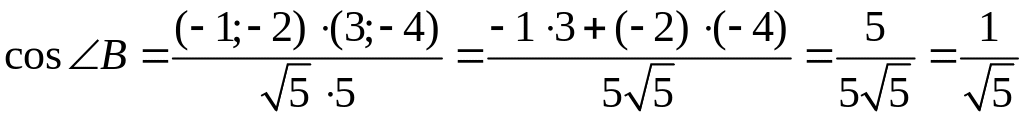
 (радиан).
(радиан).
Пример
3. Даны
координаты вершин пирамиды
![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Требуется
найти:
1) площадь грани
;
2) объем пирамиды
;
3) расстояние от вершины
.
Требуется
найти:
1) площадь грани
;
2) объем пирамиды
;
3) расстояние от вершины
![]() до плоскости, проходящей через вершины
,
и
.
до плоскости, проходящей через вершины
,
и
.
Решение. 1) Грань пирамиды является треугольником, построенным на векторах и . Найдем координаты векторов и :
![]() ,
,
![]() .
.
Площадь треугольника, построенного на двух векторах, равна половине модуля векторного произведения этих векторов. Найдем векторное произведение по формуле из раздела Справочный материал, Векторы на плоскости и в пространстве:
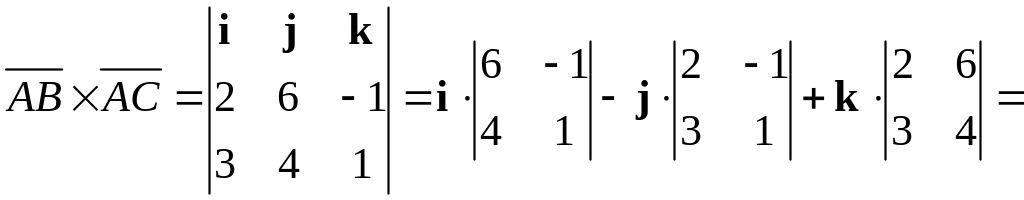
![]()
![]() .
.
Модуль векторного произведения
![]() .
.
Тогда площадь треугольника
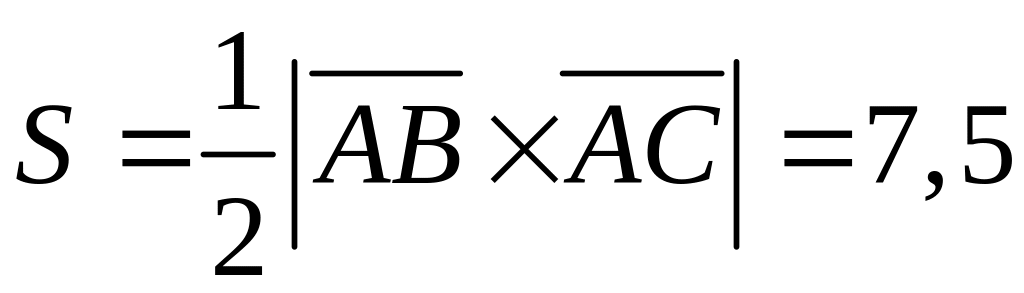 (кв.
ед.).
(кв.
ед.).
2)
Пирамида
построена на векторах
![]() ,
,
![]() и
и
![]() .
Вектор
.
Вектор
![]() .
Найдем сначала объем параллелепипеда,
построенного на векторах
,
и
.
Этот объем равен модулю смешанного
произведения этих векторов. Найдем
смешанное произведение по формуле из
раздела Справочный
материал,
Векторы на
плоскости и в пространстве:
.
Найдем сначала объем параллелепипеда,
построенного на векторах
,
и
.
Этот объем равен модулю смешанного
произведения этих векторов. Найдем
смешанное произведение по формуле из
раздела Справочный
материал,
Векторы на
плоскости и в пространстве:
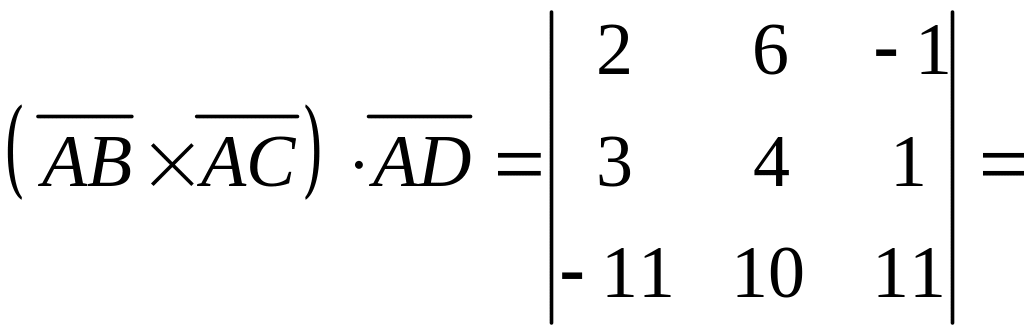
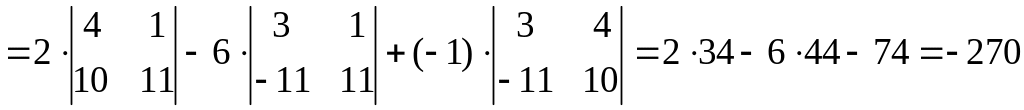 .
.
Тогда объем параллелепипеда
![]() (куб.
ед.).
(куб.
ед.).
Объем пирамиды
 (куб.ед.).
(куб.ед.).
3) Расстояние от точки до плоскости, проходящей через точки , и , равно длине высоты пирамиды , проведенной из точки к грани . Из формулы 8 (см. раздел Справочный материал, Основные формулы аналитической геометрии в пространстве) имеем:
,
откуда
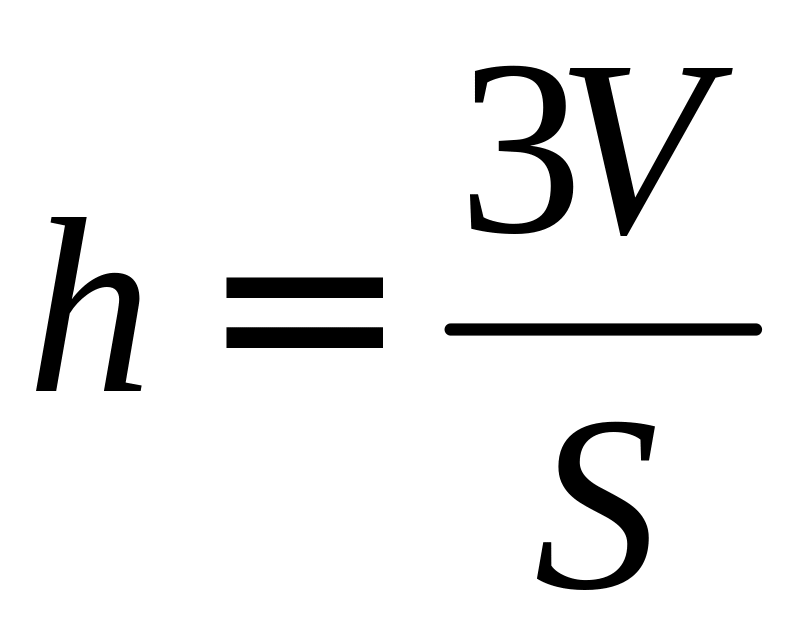 ,
,
где
– объем пирамиды,
– площадь грани
.
Подставляя в последнюю формулу ранее
найденные значения
![]() и
и
![]() ,
получим:
,
получим:
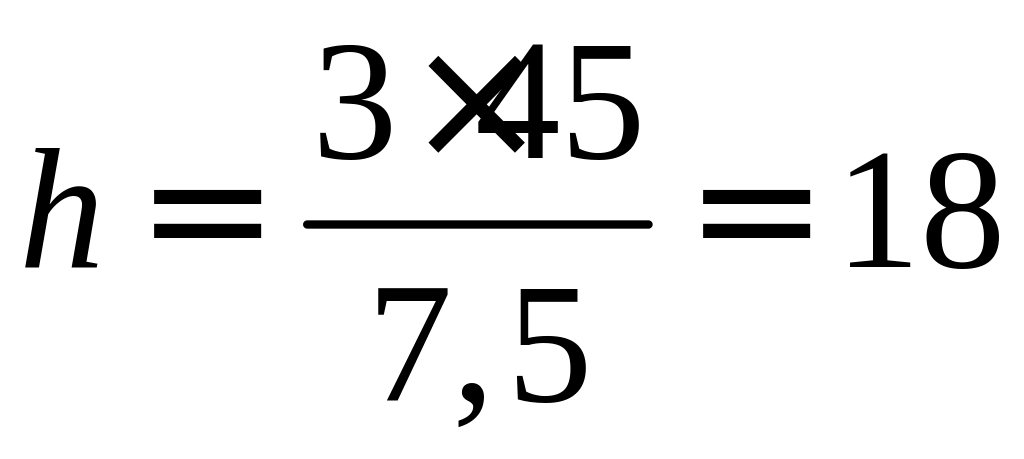 (ед.).
(ед.).
Пример 4. Решить систему трех уравнений с тремя неизвестными методом Гаусса.
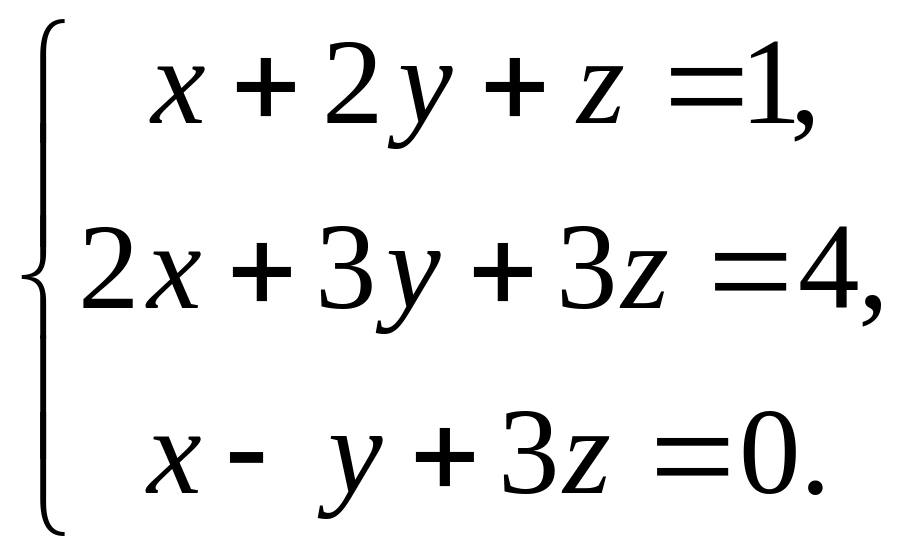
Решение. Преобразуем систему к треугольному виду. Для этого сначала исключим из второго и третьего уравнений системы переменную . Умножим первое уравнение системы на ( ) и сложим его с третьим уравнением системы. Получим:

Умножим
первое уравнение системы на (![]() )
и сложим со вторым уравнением системы:
)
и сложим со вторым уравнением системы:
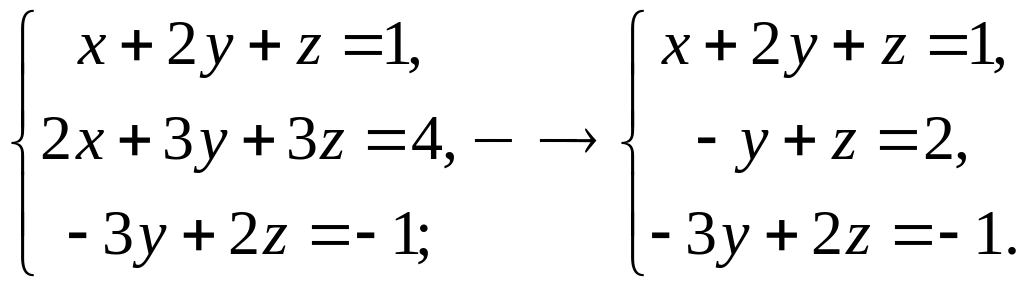
Исключим
из третьего уравнения системы переменную
.
Умножим второе уравнение системы на
(![]() )
и сложим с третьим.
)
и сложим с третьим.
Получим:
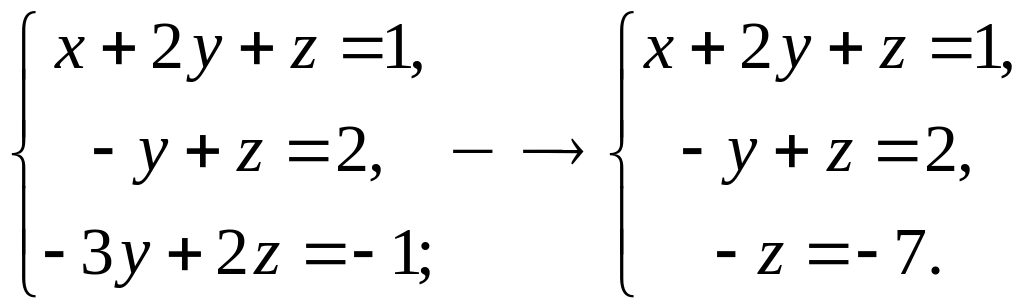
Система
приведена к ступенчатому виду.
Последовательно найдем значения
переменных, начиная с третьего уравнения
преобразованной системы:
![]() ,
,
![]() ,
,
![]() .
.
Рассмотрим пример системы, не имеющей решения.
Пример 5. Решить систему трех уравнений с тремя неизвестными методом Гаусса
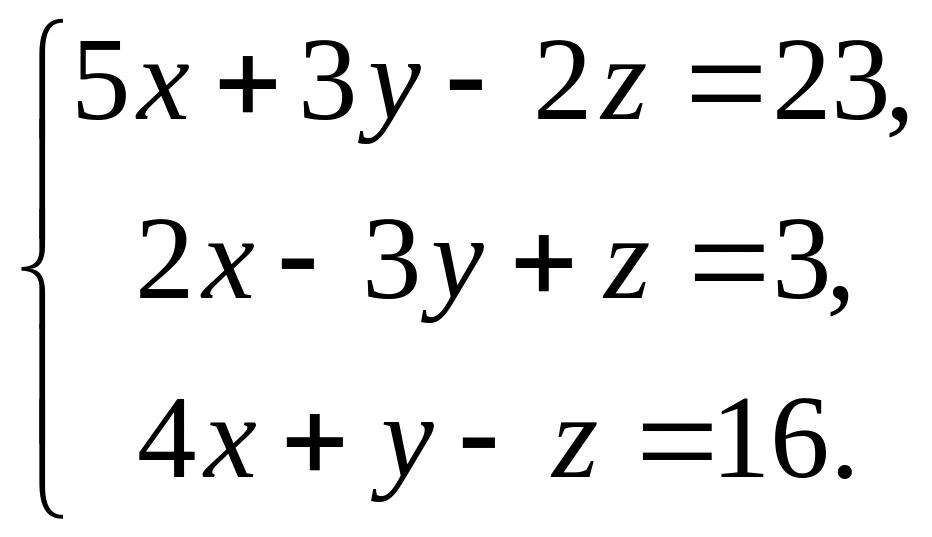
Решение. Преобразуем систему к ступенчатому виду. Для этого сначала исключим из второго и третьего уравнений системы переменную . Умножим второе уравнение системы на ( ) и сложим его с третьим уравнением системы. Получим:
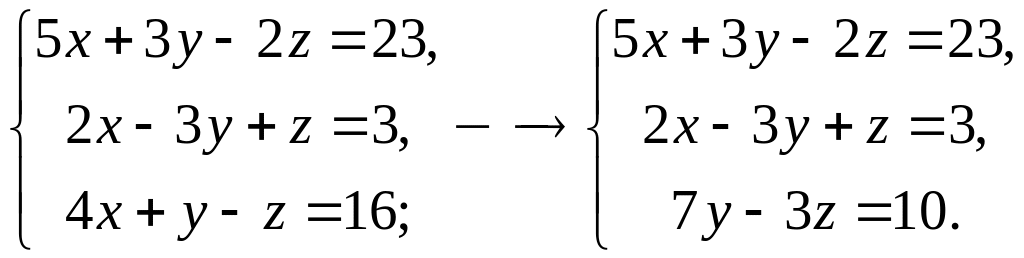
Умножим
первое уравнение системы на (
),
второе на
![]() и сложим их:
и сложим их:
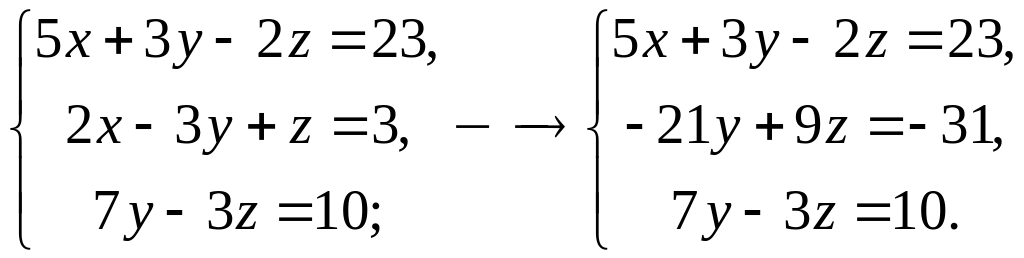
Исключим из третьего уравнения системы переменную . Умножим третье уравнение на 3 и сложим со вторым уравнением системы. Получим:

Последнее
уравнение преобразованной системы
противоречиво, т.к. привелось к неверному
равенству при любых значениях переменных
,
,
![]() .
Следовательно, данная система решений
не имеет.
.
Следовательно, данная система решений
не имеет.
