
Литература
Карта методического обеспечения дисциплины
№
|
Автор |
Название |
Издательство |
Год издания |
1 |
2 |
3 |
4 |
5 |
6.1.1 |
Шевченко Н.П. |
Алгебра и аналитическая геометрия |
ДГТУ. - Ростов н/Д |
2006 |
6.1.2 |
Зубков А.Н., Павлова М.Н |
Матрицы и их применение. Линейные преобразования. |
ДГТУ - Ростов н/Д |
2012 |
6.1.3 |
Данко П.Е.
|
Высшая математика в упражнениях и задачах. Ч.1 |
М. : ОНИКС 21 век: Мир и Образование |
2004 |
6.1.4 |
Ворович Е.И. |
Учебно-методическое пособие по подготовке к интернет экзамену |
ДГТУ. - Ростов н/Д |
2007 |
6.1.5 |
Шипачев В.С. |
Задачник по высшей математике |
М. : Высш. шк.
|
2005 |
6.6.1 |
Абуев Ф.Л. |
Программа и варианты контрольных работ для студентов первого курса заочного факультета |
ДГТУ. - Ростов н/Д |
2006 |
6.6.2 |
Шевченко Н.П. |
Программа, варианты и методические указания к контрольным работам для студентов второго курса заочного факультета |
ДГТУ. - Ростов н/Д |
2007 |
Вариант контрольной работы соответствует последней цифре номера зачетной книжки (нуль соответствует варианту №10) Контрольная работа №1
Задание №1
1.Даны
матрицы А
=
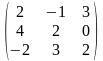 и В
=
и В
=
 .
.
Вычислить ВА+2В.
2.Даны
матрицы А
=
 и В
=
и В
=
 .
.
Вычислить АВ-3В.
3.Даны
матрицы А
=
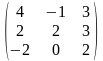 и В
=
.
и В
=
.
Вычислить АВ-3А.
4.Даны
матрицы А
=
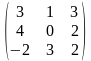 и В
=
и В
=
 .
.
Вычислить 3В + ВА.
5.Даны
матрицы А
=
 и В
=
и В
=
 .
.
Вычислить 2А + ВА.
6.Даны
матрицы А
=
 и В
=
и В
=
 .
.
Вычислить 3В + ВА.
7.Даны
матрицы А
=
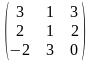 и В
=
и В
=
 .
.
Вычислить 2В + 3ВА.
8.Даны
матрицы А
=
 и В
=
и В
=
 .
.
Вычислить 3В +2 АВ.
9.Даны
матрицы А
=
 и В
=
и В
=
 .
.
Вычислить 3В + ВА.
10.Даны
матрицы А
=
 и В
=
и В
=
 .
.
Вычислить 4А + ВА.
Задание №2
Решить системы линейных алгебраических уравнений матричным способом.
1.
 6.
6.

2.
 7.
7.

3.
 8.
8.

4.
 9.
9.

5.
 10.
10.

Задание №3
Решить систему линейных алгебраических уравнений
методом Гаусса;
1.
 2.
2.

3.
4.

5.
 6.
6.
7.
8.

9.
 10.
10.
Задание №4
Найти собственные числа и собственные векторы матрицы А.
1.
 2.
2.

3.
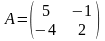 4.
4.
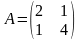
5.
 6.
6.

7.
 8.
8.

9.
 10.
10.
 .
.
Даны точки А, В, С, D.
№ варианта |
А |
В |
С |
D |
1 |
(2;-1;3) |
(-1;3;2) |
(0;1;-1) |
(-1;-3;1) |
2 |
(-2;-1;3) |
(1;3;2) |
(3;1;-1) |
(2;-3;-2) |
3 |
(0;-1;3) |
(-2;3;-1) |
(0;1;-1) |
(-1;-3;1) |
4 |
(3;-2;3) |
(-1;0;2) |
(-3;1;-1) |
(-3;-3;1) |
5 |
(1;-1-2) |
(-1;2;-2) |
(2;1;-2) |
(-1;-2;3) |
6 |
(1;-1;3) |
(-1;-2;2) |
(1;1;-1) |
(0;-3;1) |
7 |
(2;-2;3) |
(-2;3;2) |
(1;1;-1) |
(-1;-3;0) |
8 |
(-2;1;-3) |
(2;3;2) |
(3;-1;-1) |
(-1;-3;1) |
9 |
(-1;-1;3) |
(-1;3;-2) |
(-3;1;-1) |
(-1;-3;2) |
10 |
(2;-1;2) |
(-1;-3;2) |
(2;1;-1) |
(-1;-3;0) |
