Системы m линейных уравнений с n неизвестными.

1. Дана система m линейных уравнений с n неизвестными

(1)

Напишите систему:

а) с помощью знака суммирования; б) в матричном виде.

а )

б )

2. Дана система (1). Напишите основную A расширенную 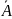матрицы коэффициентов системы.

3. Решением системы (1) называется

4. Система (1) называется совместной, если

в противном случае система

5. Теорема Кронкера – Капелли . Приведите формулировку теоремы.

6. Дана система (1). Является ли система совместной, если да, то число решений системы в каждом из указанных случаев:

а)

б)

в)

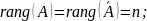
г)

7. Укажите методы решения систем линейных уравнений.

а )

б )

в )

8. Решите системы с помощью правила Крамера.

а)

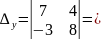
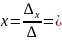
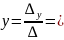
б)

в)

г)

9. Решите системы с помощью правила Крамера.

а) ;

б)

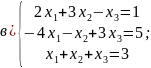
г)

10. Решите системы методом Жордана – Гаусса.

а)

б)

в)

г)

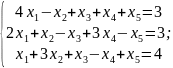
д)

е)