Описание работы

Курсовая работа представляет собой расчет нелинейной САУ с двухпозиционным регулятором. Рассчитывается система автоматической стабилизации сил натяжения левой и правой кромок движущейся ленты ткани. Принципиальная схема системы показана на рис.1.

Рис. 1.

Принцип действия САУ

Движущаяся ткань последовательно обходит ролики 1 и 2. Ролик 2 может поворачиваться вокруг вертикальной оси двигателем М со встроенным редуктором. Это приводит к изменению разности сил натяжения левой и правой кромок ткани на выходе системы. Обозначается эта разница сил – f (t). Она представляет собой ошибку регулирования, которая измеряется датчиком Д и выдается в регулятор Р в форме электрического сигнала:

, где k_D – коэффициент передачи датчика.

Регулятор Р представляет собой электрической реле и выходной сигнал описывается следующим математическим выражением:

U(t) – электрическое напряжение на выходе регулятора;

b, c – постоянные параметры статической характеристики реле.

График зависимости U (ε) показан на рис.2.

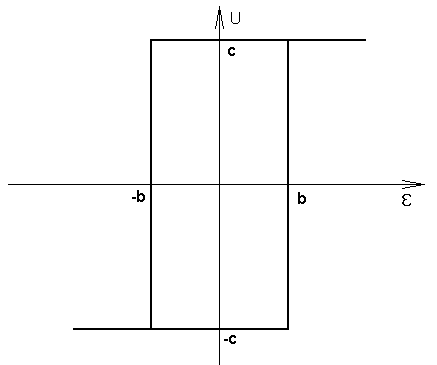
Рис. 2.

Напряжение U (t) поступает на управляющую обмотку двигателя М и обеспечивает через редуктор поворот ролика 2 в таком направлении, чтобы обеспечить уменьшение разности сил натяжения кромок ткани f (t).

Двигатель с редуктором и нагрузкой описывается уравнением:

φ (t) – угол поворота ролика 2 вокруг вертикальной оси;

f_B (t) – случайно изменяющаяся во времени разность сил натяжения левой и правой кромок ткани на выходе системы, т.е. перед роликом 1 (возмущающее воздействие);

k₁ – коэффициент передачи по управляющему воздействию;

k₂ – коэффициент передачи по возмущающему воздействию;

Т – постоянная времени.

Разность сил натяжения ткани на выходе системы за роликом 2 вблизи датчика Д связана с разностью сил натяжения ткани на входе системы соотношением:

k₃ – постоянный коэффициент преобразования угла поворота валика 2 в разность сил натяжения.

Величину напряжения C на выходе регулятора необходимо определить в процессе выполнения работы.

Исходные данные (7 вариант)

K_D = 0.134 В / Н

K₁ = 0.247 рад / сּВ

K₂ = 0.0728 рад / сּН

K₃ = 131 Н / рад

T = 0.46 c

b = 0.0104 B

Δ = 0.0129 рад

Задание

1. Построить структурную схему рассматриваемой системы автоматического регулирования. Преобразовать структурную схему таким образом, чтобы на ней было показано задающее воздействие g = 0 (соответствует идеальному алгоритму управления f (t) = 0), и чтобы при этом возмущающее воздействие поступало в замкнутый контур в одном месте.

2. С целью исследования автоколебаний привести схему к расчетной, содержащей безинерционный нелинейный элемент и линейную часть. При выполнении этого задания считать, что f (t) = 0, т.к. автоколебания представляют собой свободное движение системы.

3. Используя метод гармонической линеаризации получить гармоническую передаточную функцию нелинейного элемента.

4. Используя уравнение гармонического баланса, доказать что при любом С в системе возникают устойчивые автоколебания. Найти наибольшую величину С, при которой амплитуда колебаний ролика не превосходит допустимого значения . Определить частоту и амплитуду этих колебаний.

5. Построить зависимость амплитуды и частоты автоколебаний от величины напряжения регулятора, выбрать рабочее значение этого напряжения.

Расчёт

1. Построим структурную схему системы, для чего сначала найдем передаточные функции всех элементов системы:

Регулятор:

Датчик:

Двигатель:

Рамка:

В результате получаем структурную схему системы, изображенную на рис.3.

Рис.3.

Преобразуем структурную схему таким образом, чтобы возмущающее воздействие поступало в замкнутый контур управления в одном месте и покажем задающее воздействие g(t) = 0. Преобразованная схема изображена на Рис. 4.

Рис.4.

2. Для применения метода гармонической линеаризации приведем схему к расчетной, т.е. содержащей безинерционный нелинейный элемент и собранную в одно звено линейную часть. Расчетная схема изображена на рис.5.

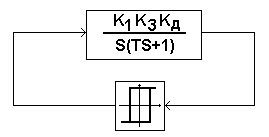
Рис. 5.

3. Метод гармонической линеаризации состоит в том, что автоколебания в системе ищутся в виде гармонического сигнала, т.е.:

а – амплитуда автоколебаний

ω – частота автоколебаний

Заменим нелинейное звено эквивалентным линейным с передаточной функцией:

– коэффициенты гармонической линеаризации

Для реле с гистерезисом:

4. Для доказательства того, что при любом с  0 в системе возникают устойчивые автоколебания воспользуемся графическим методом Гольдфарба. Из метода следует, что если равенство:

существует, т.е. соответствующие годографы пересекаются, то в системе возникают автоколебания. Для выяснения вопроса о пересечении годографов рассчитаем и построим их:

Видно, что мнимая часть годографа Z(a) не зависит от a, и следовательно он будет представлять из себя прямую параллельную действительной оси. Расстояние до нее зависит только от параметров статической характеристики нелинейного элемента. В частности, асимптотически приближается к оси при увеличении значения с.

Рис. 6.

Из графика видно, что пересечение годографов будет происходить при любом значении с, т.е. в системе всегда будут наблюдаться автоколебания.

Найдем такое значение с, при котором амплитуда колебаний ролика не превышает Δ, а это значит, что амплитуда автоколебаний на входе системы не превышает a_max.

Соответствующее этой амплитуде значение с будем искать, пользуясь уравнением гармонического баланса:

Решая систему получаем:

При a = a_max :   

5. При построении зависимостей ω(с) и а(с) воспользуемся только что полученными уравнениями:

Задаваясь значениями ω можно получить значения а и с. Построим эти зависимости:

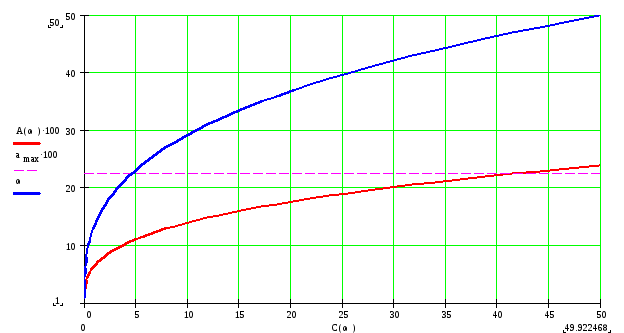
Рис. 7.

Выбираем рабочее значение напряжения регулятора с = 40 В.

Выводы.

В результате исследования автоколебаний системы

1. Построена структурная схема рассматриваемой системы управления.

2. Выведена передаточная функция линейной части системы управления.

3. С помощью метода гармонической линеаризации выведена гармоническая передаточная функция нелинейной части системы управления.

4. Доказано, что при любом с в системе будут иметь место устойчивые автоколебания.

5. Выбрано рабочее значение регулятора с = 40 В.