Добавил:

Vezen Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Коломенский институт филиал МГМУ

Предмет:

Теоретические основы электротехники

Файл:

ТОЭ - Расчет линейных электрических цепей переменного тока

.pdf

Скачиваний:

Добавлен:

20.06.2014

Размер:

829.16 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 84 5 6 7 8 > Следующая >>>

3. Расчет разветвленных цепей синусоидального тока комплексным методом

3.1. Общие сведения

Переход от вещественных синусоидальных функций времени токов и напряжений к их изображению в комплексной форме записи позволяет распространить методы расчета разветвленных цепей постоянного тока на расчет разветвленных цепей синусоидального тока.

Каноническая форма уравнений метода узловых напряжений для случая трех независимых узлов имеет вид

Y11 U&10 –Y12 U&20 –Y13 U&30 = J&11 ;

–Y 21 U&10 +Y 22 U&20 –Y 23 U&30 = J&22 ;

–Y 31 U&10 –Y 32 U&20 +Y 33 U&30 = J&33 ,

где Y11 ; Y 22 ; Y 33 – собственные комплексные проводимости ветвей, принадлежащих узлам, Y12 =Y 21 ; Y 23 =Y 32 ; Y13 =Y 31 – общие комплексные проводимости ветвей одновременно принадлежащих двум узлам, J&11 ; J&22 ; J&33 – узловые токи.

Каноническая форма уравнений метода контурных токов для случая трех независимых контуров имеет вид

Z11 I&11 + Z12 I&22 – Z13 I&33 = E&11 ;

		Z 21 I&11 + Z 22 I&22 + Z 23 I&33 =E&22 ;
		Z 31 I&11 + Z 32 I&22 + Z 33 I&33 =E&33 ,
где Z11	;	Z 22 ; Z 33 – собственные комплексные сопротивления контуров,
Z12 =Z 21	;	Z 23 =Z 32 ; Z13 =Z 31 – общие комплексные сопротивления ветвей од-

новременно принадлежащих двум контурам, E&11 ; E&22 ; E&33 – собственные э. д. с. контуров.

Правила получение узловых и контурных уравнения остаются такими, как в цепях постоянного тока.

Схема и граф обобщенной ветви цепи синусоидального тока показаны на рис. 3.1. Уравнения Кирхгофа в матричной форме для электрической цепи со схемой, имеющей b обобщенных ветвей и q узлов, имеют вид

A I& = 0 ;

B U& = 0.

Матрицы соединений (инциденций) А и главных контуров В составляются по тем же правилам, что в цепи постоянного тока.

Матрицы э. д. с. ветвей Eb , токов

I&b

источников тока J&b формируются по

J&b

тем же правилам, что для цепи постоян-

Y b =

ного тока. Коэффициенты в этих мат-

Z b

E&b

рицах– комплексные действующие зна-

чения. Коэффициенты в матрицах со-

противлений – комплексные сопротив-

ления Zb , в матрицах проводимостей –

Рис. 3.1

комплексные проводимости Y b ветвей.

Матрицы приобретают вид Zb и

Yb .

Матричное уравнение метода узловых напряжений для цепи синусои-

дального тока имеет вид

A Yb A

T &

Un0 = −A YbEb + A Jb .

Обозначив через Ynn = Ab Yb AT

квадратную матрицу комплексных уз-

ловых проводимостей,

через Jnn

= − A YbEb

+ A Jb столбцевую матрицу ком-

плексных действующих значений узловых токов, получим узловые уравнения в матричной форме

YnnU& n0 = J&nn .

Решение этого уравнения

U& n0 = Ynn−1 J&nn

определяет матрицу комплексных действующих значений узловых напряжений. Далее рассчитываются напряжения

&	T &	,	&	&	&
U	= A Un0	,	Ub = U + E
и токи
&	&		&	&	&
Ib = YbUb ,			I	= Ib − J .

Матричное контурное уравнение для цепи синусоидального тока имеет вид

B ZbBT I&nn = −B ZbJ&b + B E&b .

Обозначив через Znn = B ZbBT квадратную матрицу комплексных контурных сопротивлений, через E& nn = −B ZbJ&b + B E&b матрицу комплексов действующих значений э. д. с. контуров, получим контурное уравнение в матричной форме

Znn &Inn = E&nn .

Решение этого уравнения

&Inn = Znn−1 E& nn

определяет матрицу комплексных контурных токов. Далее рассчитываются токи ветвей:

I& = BT I&nn ; I&b = I& + J& ,

и напряжения:
&	& & &		&
Ub = ZbIb ; U = Ub		−E.
3. 2. Решение типовых задач
Задача. 3.1
На рис. 3.1 показан фрагмент цепи синусоидального тока.
Найти действующее значение напряжения U& , ес-			&			Z
π					E	Z	I&
ли E& = 220 В; I&=15e− j 6 А; Z =4 + j 2 Ом.


Решение
Назначаем положительные направления тока I&		и			U&
напряжения U& .				Рис. 3.1

Уравнение второго закона Кирхгофа для принятого на рис. 3.1 направления обхода контура имеет вид

U& – I& Z =– E& .

Откуда

− j π

U& = I& Z – E& = 15e 6 – 220 = – 267,6 – j 47,2 В.

Действующее значение напряжения равно:

U = U& = 271,8 В.

Задача. 3.2
На рис. 3.2 показан фрагмент цепи синусоидального тока.
Найти ток I&, если U& = 380 В; E& = 220 e j120o В;		I&
J& = − j 20 А; Z =5 – j 2 Ом.			I&b	J&
Решение. Назначаем положительные на-			Z	J&
правления токов ветвей и напряжения U& .	U&		Z
правления токов ветвей и напряжения U& .	U&
Уравнения Кирхгофа имеют вид			E&
– I&+ J&+ I&b = 0;
– I&+ J&+ I&b = 0;
U& – I&b Z =– E& .
U& – I&b Z =– E& .
Из второго уравнения находим:		Рис. 3.2

&	U& + E&		380	+ 65,18	− j210
Ib =		=				=91,25 – j 5 А.
Ib =	Z	=		5 − j2		=91,25 – j 5 А.
	Z			5 − j2

Из первого уравнения получаем:

I&=J&+ I&b = –j 20 + 91,2 – j 5 = 91,25 – j 25 = 94,75 e− j15,6o А.

Программа расчета в пакете Mathcad приводится ниже.

. .

← Исходные данные.

380

220.e

e = 65.185

210.121i j

j .20

ib = 91.247

5.525i

← Расчет тока ветви.

i = 91.247

25.525i I

I = 94.75

← Расчет тока I& в показа-

ψi

180

.arg(i)

ψi =

15.628

тельной форме записи. Ар-

гумент в градусах.

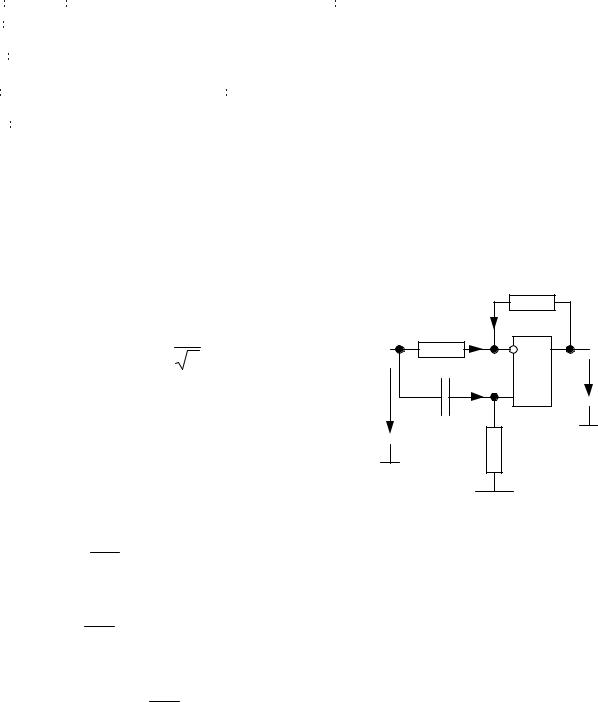
Задача 3.3

Цепь со схемой рис. 3.3 содержит идеальный операционный усилитель ОУ. Па-

раметры цепи	R1 =R2 =R3 =R = 47 кОм, С = 0,068 мкФ. Найти напряжение
uвых , если uвх	=10sin 314t В.

Решение

Назначаем положительные направления токов (рис. 3.3). U&вх = 102 В. Поскольку

усилитель идеальный (токи входов равны нулю), уравнение по законам Кирхгофа имеют вид

I&1 + I&2 = 0;

–U&вх + I&С Z = 0;

–U&вх + I&1 R1 – I&2 R2 +U&вых = 0,

где Z = R − ωjC = (4,7 – j 4,68) 10 4 Ом.

Из второго уравнения находим

I&С = U&Zвх .

По закону Ома

U&R3 = I&С R3 =U&Zвх R3 .

		R2
	R1	i2
	C i1	∞
uвх	C i1	uвых
uвх	iC	ОУ
	iC

		R3
	Рис. 3.3

Токи

I& =U&вх −U&R3 ;

1 R1

I&1 = – I&2 .

Комплексное действующее значение выходного напряжения определяется из уравнения Кирхгофа

U&вых = U&вх – I&1 R1 + I&2 R2 .

Программа расчета в пакете Mathcad приводится ниже. Расчет ведется относительно комплексных амплитуд.

Ubxm

47.103 C

0.068.10 6 ω

314

ubxm

Ubxm

j .

z = 4.7 104

4.683 104 j

ω.C

uR3m

ubxm

i1m

ubxm

uR3m

i2m

i1m

uvxm

ubxm

i1m.R

i2m.R

uvxm= 0.035 + 10j

Uvxm

uvxm

Uvxm= 10

ψu

180

.arg(uvxm) ψu = 89.797

Амплитуда выходного напряжения

Uвых m = 10 В.

Начальная фаза

ψu = 89,8°.

Мгновенное значение выходного напряжения uвых =10sin(314t +89,8o ) В.

Задача 3.4

←Исходные данные.

←Комплексная амплитуда входного напряжения.

←Расчет комплексного сопротивления Z .

←Расчет напряжения на резисторе R3.

←Расчет тока ветвей.

←Расчет выходного напряжения в показательной форме записи. Аргумент в градусах.

В цепи со схемой рис. 3.4 найти комплексные действующие значения токов ветвей. Действующее значение синусоидального напряжения U = 220 B. Активные сопротивления: R1 = 91 Ом; R3 = 510 Ом; R4 = 820 Ом. Реактивные сопро-

тивления: X1 = ω L1 = 240 Ом; X2 = 1/ ω C2 = 150 Ом; X3 = 1/ ω C3 = 190 Ом.

Расчет выполнить методом узловых напряжений.

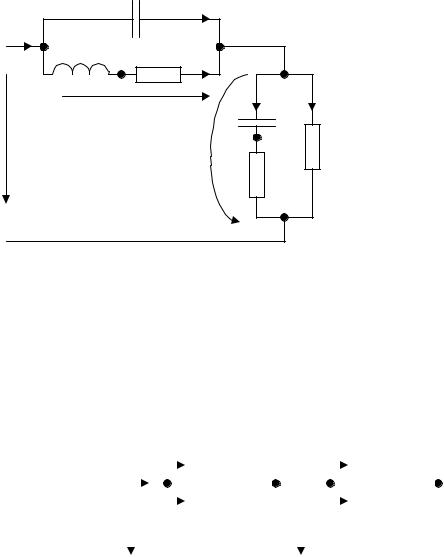
		C2	i2
1 i				2
L1	a	R1	i1	3
	a	R1	i1	3
	u12			i3 C3	i4

u34

Рис. 3.4

Решение

Комплексные сопротивления ветвей рассчитаны в задаче 2.5. Имеем:

= R

+ jX

= 91 + j240 = 256,67e j69o Ом;

Z 2

= − jX2

= − j150 = 150e− j90o

Ом;

= R

− jX

= 510 − j190 = 544,24e− j20,4o

Ом;

Z 4

= R4 = 820 Ом.

I&2

Z 2

I&3

Z 4

Для расчета

схему

цепи

удобно представить

как

на

рис. 3.5.

I&1

U&34

I&4

Рассчитываем

методом

узловых напряжений.

Узловое уравнение имеет вид

Рис. 3.5

(

− (

Z 2

Z 3

Z 4

)U34

Z 2

)U = 0 ,

откуда

U&34

Z 2

Z 3

Z 4

Токи ветвей:

I&1 =

U& −U&34

= 0,46e− j97,2o А; I&2 =

U& −U&34

= 0,78e j62o А;

I&3 =

U&34

= 0,24e j 45,6o А; I&4 =

U&34

= 0,16e j 25o А;

Z 4

Z 3

I& = I&1 + I&2 = 0,39e j37,4o А.

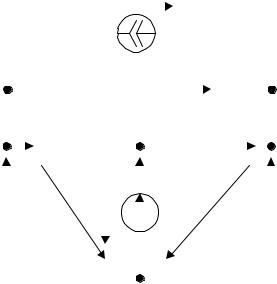
Задача 3.5

Для цепи со схемой рис. 3.6 найти

U&J

комплексы

действующих

значений

токов ветвей, если

J&1

Z 4

I&4

Z1 = j10 Ом, Z 2 = 6 + j8 Ом,

Z 3 = 3 Ом, Z 4 = Z1 , Z5 = − j7 Ом,

Z 2

J& = 5А, E&

= j110 В.

Проверить

выполнение

баланса

I&3

I&5

мощностей.

U& U&20

Решение

Z 3

Назначаем

положительные направ-

U30

ления токов ветвей.

Выбираем в качестве базисного узел

0. Напряжение узла 2 относительно

Рис. 3.6

базисного U&20 = E& .

Напряжения U&10 и U&30 определяем методов узловых напряжений. Узловые уравнения имеют вид:

Y U&

−Y U&

= J& ;

−Y U&

+Y U&

= J&

где Y11 =

1 +

= 0,33 − 0,2 j

Ом–1;

Z 3

Z 4

j10

j10 3

Y 33 =

= 0,06 − 0,037 j

Ом–1 – собственные

Z 2

Z 4

+ j8

− j7

j10

комплексные проводимости узлов 1 и 3, Y12

= − 0,1 j Ом–1;

j10

Y13 =

= − 0,1 j Ом–1; Y 31 =Y13

; Y 32

= 0,06 −0,08 j Ом–1

j10

Z 2

+ j8

Z 4

– общие комплексные проводимости,

J&11 = J&1 = j5 А; J&33 = −J&1 = − j5 А узловые токи.

Поскольку U&20

= E& , решив матричное уравнение

−Y

−1

U10

Y12 E

−

−Y

найдем значения узловых напряжений:

U&10 = 2 − j42,4 В; U&30

= 35,32 − j128,13 В.

Токи ветвей определяются по уравнениям:

I&1 =

− E&

= −4,24 +

10,8 j =

11,6e j111 А;

I&2

−U&

+ E&

= 14,73

+1,71 j = 14,83e j6,6 А;

I&3

−U&10

= −0,67 +14,13 j =14,15e j92,7o А;

Z 3

I&4

−U&

= 8,57 + 3,33 j = 9,2e j21 А;

Z 4

I&5 =

−U&30

= −18,3 −5,05 j =18,99e− j164o А;

I& = I&2

− I&1

=18,97 – 9,09 j = 21,03e− j25,6o А.

Баланс мощностей. Комплексная мощность источников

Sист= E&I + (U&10 −U&30 )J1 =1,92 103 +1,43 103 j ВА.

Комплексная мощность потребителей

Sпот = I12 Z1 + I22 Z 2 + I32 Z 3 + I42 Z 4 + I52 Z 5 =1,92 103 +1,43 103 j ВА.

Здесь

J1 ,

– сопряженные комплексные значения.

Баланс мощностей выполняется, Sист = Sпот.

Программа расчета в пакете Mathcad приводится ниже.

.10 z2

j .8

j .7 ← Исходные данные.

110

180

← Расчет собственных и общих

y11

y33

комплексных проводимостей.

y11

= 0.33

0.2i

y33 = 0.06

0.04i

y12

y32

y13

y31

y13

y12

0.1i

y32 = 0.06

0.08i

y13 =

0.1i

← Расчет комплексных узловых на-

u10

y11

y13 .

y12 e

пряжений.

y32.e

u30

y31

y33

u10 = 2

42.4i

u30 = 35.32

128.13i

u10

ψi1

rg.arg(i1)

ψi1 = 111.43

4.24 + 10.8i

I1 = 11.6

u30

ψi2

rg.arg(i2)

ψi2 = 6.64

= 14.73 + 1.71i

I2 = 14.83

u10

ψi3

rg.arg(i3)

ψi3 = 92.7

0.67 + 14.13i

I3 = 14.15

u10

u30

ψi4

rg.arg(i4)

ψi4 = 21.24

= 8.57 + 3.33i

I4 = 9.2

u30

ψi5

rg.arg(i5)

ψi5 =

18.3

5.05i

I5 = 18.99

164.59

ψi

rg.arg(i)

i = 18.97

9.09i

I = 21.03

ψi =

25.59

(u10

u30).

se = 1.92 103 + 1.43 103 i

I12.z1

I22.z2

I32.z3

I42.z4

I52.z5

sz = 1.92 103 + 1.43 103 i

Задача 3.6

← Расчет комплексных токов ветвей.

Баланс мощностей.

←Расчет комплексной мощности источников.

←Расчет комплексной мощности нагрузок.

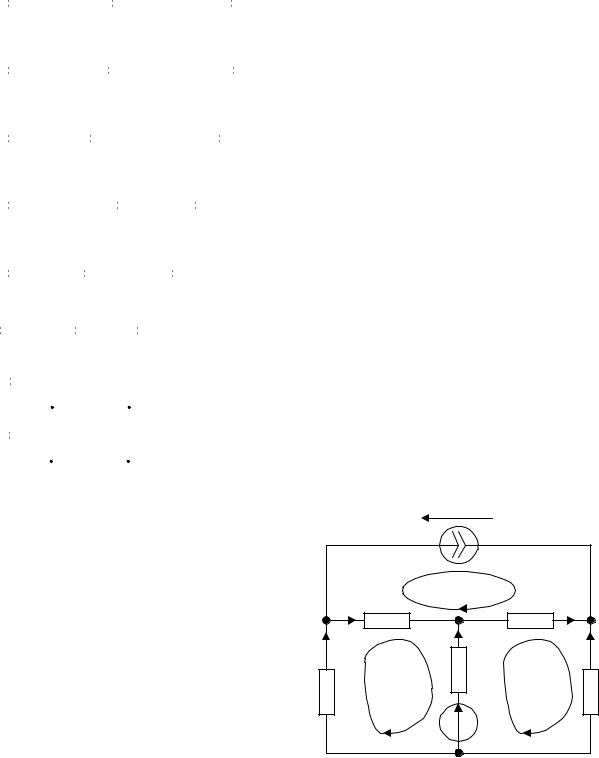
Для цепи со схемой рис. 3.7 найти					U&J
комплексные действующие	значения				J&1
токов ветвей. Комплексные сопротив-					J&1
ления: Z1 = j10 Ом, Z 2 = 6 + j8 Ом,		I&1	Z1	J&1		Z 2	I&2
Z 3 = 3 Ом, Z 4 = Z1 , Z5 = − j7 Ом,		I&1	Z1			Z 2	I&2
Z 3 = 3 Ом, Z 4 = Z1 , Z5 = − j7 Ом,					I&4
J&1 = 5А, E&4 = j110В.		I&3			I&4		I&5
Проверить выполнение баланса мощ-					Z 4
ностей.		Z 3	I&11		E&4	I&22	Z5
Решение					E&4
Назначаем положительные направле-
ния токов ветвей. Определяем неза-				Рис. 3.7
висимые контуры с токами I&11 и I&22				Рис. 3.7
висимые контуры с токами I&11 и I&22

как показано на рис. 3.7. Ветвь с источником тока не должна входить в эти контуры. Контурный ток J&1 равен току источника тока.

Уравнения относительно контурных токов I&11 и I&22 имеют вид:

Z11I&11 + Z12 I&22 + Z13 J&1 = −E&4 ;

Z 21I&11 + Z 22 I&22 + Z 23 J&1 = E&4 ,

где:

Z11 = Z1 + Z 3 + Z 4 = j10 + 3 + j10 = 3 + j20 Ом;

Z 22 = Z 2 + Z5 + Z 4 = 6 + j8 – j7 + j10 = 6 + j11 Ом;

Z12 = −Z 4 = – j10 Ом, Z 21 = Z12 ;

Z13 = −Z1 = – j10 Ом;

Z 23 = −Z 2 = – 6 – j8 Ом.

Решение уравнения

−1 − E&

Z11

Z12

− Z

11 =

Z 22

I&22

Z 21

E&4

− Z 23 J&1

дает значения контурных токов:

I&11 = 2,26 + j 3,98 А;

I&22 = 11,72 + j 7,29 А.

Токи ветвей:

I&1 = I&11 − J&1 = −2,74 + j3,98 = 4,83e j124,5o

А;

I&2

= I&22 − J&1 = 6,72 + j7,29 = 9,91e j 47,3o

А;

I&3

= I&11 = 2,26 + j3,98 = 4,58e j60,4o

А;

I&4

= I&22 − I&11 = 9,46 + j3,3 =10,02e j19,25o

А;

I&5

= −I&22 = −11,72 − j7,29 =13,8e− j148,1o

А.

Рассчитываем баланс мощностей.

Комплексная мощность источников

Sист =U&J J1 + E&I4 ,

где U&J – напряжение на источнике тока,

J1; I4

– сопряженные комплексные то-

ки. Напряжение

U&J

= −I&1 Z1 − I&2 Z 2

= 90,84e− j50,5o

В.

Подставляя данные, получаем

Sист = 652,26 + j689,82 ВА.

Комплексная мощность Sпот потребителей:

Sпот= I12 Z1 + I22 Z 2 + I32 Z 3 + I42 Z 4 + I52 Z 5

= 652,26 + j689,82 ВА.

Получили Sист = Sпот, баланс мощностей выполняется. Программа расчета в пакете Mathcad приводится ниже.

<<< < Предыдущая 1 2 34 / 84 5 6 7 8 > Следующая >>>

Соседние файлы в предмете Теоретические основы электротехники

#
20.06.20141.01 Mб91Лекции Теоретические основы электротехники (Основы теории цепей).doc
#
20.06.2014829.16 Кб59ТОЭ - Расчет линейных электрических цепей переменного тока.pdf
#
20.06.2014412.09 Кб31ТОЭ - Расчет линейных электрических цепей постоянного тока.pdf