2-й семестр / Электричество и магнетизм. Курс лекций. Задерновский

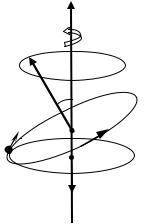
51

вих сильном намагничивании в относительно слабых внешних полях. К тому же у ферромагнетиков величина χ не постоянна, а зависит от напряженности внешнего поля.

Особенности поведения различных магнетиков объясняются различиями

вих магнитной структуре. Рассмотрим подробнее, как ведут себя атомы в маг-

нитном поле. Как уже отмечалось, движущийся по орбите электрон, подобно круговому току, имеет магнитный

нитный момент атома, противоположный полю.

Описанное явление называется диамагнитным эффектом и присутствует во всех магнетиках. Однако, этот эффект практически не заметен в парамагнетиках и ферромагнетиках, атомы которых обладают собственными магнитными моментами. Ориентация этих моментов во внешнем поле создает намагниченность параллельную этому полю, и значительно превышающую намагниченность, связанную с диамагнитным эффектом.

В диамагнетиках суммарный магнитный момент всех электронов в атоме, и, соответственно, магнитный момент атома, равен нулю. Поэтому их намагничивание обусловлено только диамагнитным эффектом.

Поведение парамагнетиков в магнитном поле аналогично поведению полярных диэлектриков в электрическом поле. Магнитные моменты атомов стремятся ориентироваться вдоль линий поля. Этому процессу мешает тепловое движение. Изменение интенсивности теплового движения с температурой обуславливает и температурную зависимость χ. Она оказывается обратно пропорциональной абсолютной температуре.

Как в парамагнетиках, так и в диамагнетиках намагниченность линейно зависит от напряженности внешнего поля. Их магнитная восприимчивость χ (а также и μ) остаются постоянными при данной температуре.

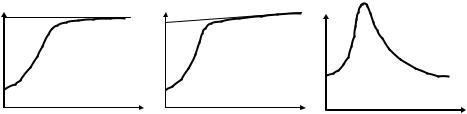
Рис. 5.8

Несколько иначе происходит намагничивание ферромагнетиков. Как показали опыты А.Г. Столетова (1872 г.), их намагниченность зависит от Н сложным образом. Типичная зависимость J от Н для изначально не намагниченного образца показана на рисунке 5.8а. Это так называемая, основная кривая намагничивания. По мере возрастания Н намагниченность J сначала растет быстро (и нелинейно), затем медленнее и, наконец, достигается магнитное насыщение, значение J уже не зависит от напряженности H.

График зависимости В от Н (рис. 5.8 б) отличается от графика J=f(H) отсутствием горизонтальной участка: как только наступает насыщение, магнит-

напряженности магнитного поля. Из первых двух графиков вытекает зависимость от Н, показанная на рис. 5.8 в). Максимальные значения соответствуют области наиболее быстрого роста намагниченности. Численные значения μмакс. для ферромагнетиков очень велики: макс 103 106.

Описанное поведение ферромагнетиков объясняется наличием в них областей самопроизвольно (спонтанно) намагниченных до насыщения. В этих областях, называемых доменами, магнитные моменты атомов под действием определенных внутренних сил выстраиваются параллельно друг другу. При этом энергетически выгодным оказывается такое расположение доменов, при котором суммарный магнитный момент образца равен нулю.

Уже в слабом магнитном поле начинается смещение границ между доменами. При этом домены, намагниченность которых близка по направлению к направлению внешнего поля, растут за счет других доменов. В результате общая намагниченность образца быстро увеличивается. Вторая стадия процесса – поворот магнитных моментов доменов в направлении поля соответствует более медленному росту намагниченности вплоть до достижения насыщения.

Интересно, что описанные процессы являются необратимыми. Если намагнитить ферромагнетик до насыщения, а затем уменьшать напряженность

53

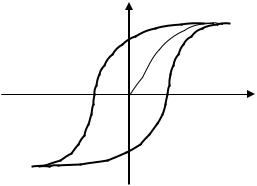
магнитного поля, то намагниченность будет изменяться по кривой, лежащей выше основной кривой намагничивания (рис.5.9). При Н = 0 в ферромагнетике наблюдается остаточная намагниченность Jост, что объясняет существование постоянных магнитов. Намагниченность обращается в нуль только в размагни-

ниченностью.

Различные ферромагнетики дают разные гистерезисные петли. В зависимости от значения коэрцитивной силы различают магнито-мягкие и магнитожесткие ферромагнетики. Магнито-мягкие ферромагнетики отличаются малым значением коэрцитивной силы. Они легко перемагничиваются и используются при изготовлении трансформаторов, электрических машин и т.п. Из магнитожестких ферромагнетиков изготавливаются постоянные магниты.

Как показывает опыт, при достаточно высоких температурах доменная структура ферромагнитных веществ разрушается. Для каждого ферромагнетика есть определенная температура, при которой он теряет ферромагнитные свойства. Эта температура называется точкой Кюри. При температурах выше точки Кюри ферромагнетик ведет себя так же, как обычный парамагнетик. Для железа, например, эта температура равна 768°С, а для никеля - 365°С.

ЛЕКЦИЯ 6. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. УРАВНЕНИЯ МАКСВЕЛЛА

6.1. Явление электромагнитной индукции. Правило Ленца. Закон Фарадея

Открытие Эрстедом магнитного поля, создаваемого проводником с током, навело английского ученого Фарадея на мысль о возможности противоположного явления. Он предположил, что с помощью магнитного поля можно создать электрический ток. После многочисленных опытов Фарадею в 1831 году удалось обнаружить появление электрического тока в замкнутом проводящем

54

контуре при изменении магнитного потока Ф через поверхность, ограниченную данным контуром. Это явление называют электромагнитной индукцией а, полученный таким образом ток - индукци-

онным током.

Схема одного из опытов Фарадея показана на рис. 6.1. При движении постоянного магнита внутрь катушки, замкнутой на гальванометр, в ней возникает индукционный ток. При движении в обратном направлении меняется и направление тока. Появление тока указывает на то, что в цепи начинает действовать электродвижущая сила, называемая ЭДС индукции εi .

Из определения магнитного потока dФ BdS cos видно, что его величина может изменяться не только при увеличении или уменьшении индукции магнитного поля, как в рассмотренном выше опыте. Изменение потока происходит и при изменении площади контура, находящегося в постоянном магнитном поле (например, при деформации контура). К такому же результату приво-

Ряд других опытов показал, что при любом изменении магнитного потока через замкнутый контур в нем появляется индукционный ток. Направление этого тока можно определить по, так называемому, правилу Ленца: индукционный ток всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего этот ток.

значно вытекает указанное на рисунке направление тока (против часовой стрелки).

55

Существует и более общая формулировка правила Ленца: индукционный ток всегда направлен так, чтобы противодействовать причине его вызываю-

щей. Применим это правило к рассматриваемому нами случаю. В качестве при-

чины возникновения тока будем рассматривать внешнюю силу F , обуславливающую движение перемычки (см. рис. 6.2). Тогда следует сделать вывод, что должна появиться некая противодействующая сила, направленная в противоположную сторону. Действительно, на перемычку с током будет действовать сила Ампера. Определив, таким образом, направление этой силы, нетрудно, используя правило левой руки, установить направление индукционного тока.

Обобщая результаты своих опытов, Фарадей установил, что величина индукционного тока, а, значит, и ЭДС электромагнитной индукции, не зависит от способа, которым осуществляется изменение магнитного потока, и определяется только скоростью его изменения, т. е.

i dt

Данное соотношение носит название закона электромагнитной индукции Фарадея. Знак минус в этом законе иллюстрирует правило Ленца. В са-

мом деле, если нормаль к контуру n выбрать так, как показано на рисунке 6.2,

индукционный ток будет создавать отрицательный магнитный поток, то есть поток, направленный противоположно нормали и внешнему магнитному потоку. Если перемычку перемещать в противоположную сторону поток Ф будет

направление и создаст положительный поток вдоль нормали n , противодействуя тем самым уменьшению внешнего магнитного потока.

Если индукционный ток возникает в катушке, состоящей их N витков, ЭДС индукции будет равна сумме ЭДС, возникающих в каждом витке. Тогда закон электромагнитной индукции можно записать в виде

где Ψ N Φ - полный магнитный поток или потокосцепление.

6.2. Явление самоиндукции. Индуктивность Самоиндукция это частный случай явления электромагнитной индукции.

Самоиндукцией называют возникновение ЭДС индукции в проводящем конту-

Индуктивность соленоида можно существенно увеличить поместив в него сердечник из ферромагнетика с магнитной проницаемостью μ. При этом в μ раз увеличится индукция магнитного поля В, а выражение для индуктивности будет выглядеть следующим образом

Заметим, что в этом случае индуктивность уже не является постоянной величиной. Как было показано ранее, в ферромагнетике μ сложным образом зависит от напряженности магнитного поля. Таким образом, и индуктивность будет, в конечном счете, за-

ствует против ЭДС источника ε и препятствует быстрому увеличению тока. Несложный расчет показывает, что сила тока в цепи I изменяется со временем по закону

Если теперь отсоединить источник, переведя ключ в верхнее положение

отношения R/L. Чем больше индуктивность и меньше активное сопротивление цепи, тем медленнее эти процессы.

58

6.3. Взаимная индукция

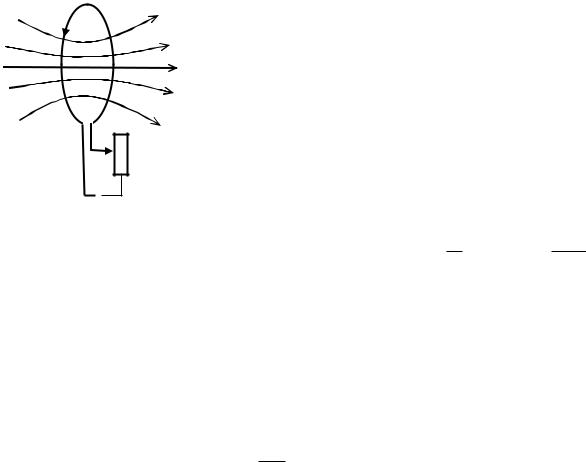
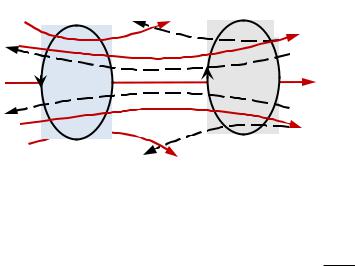
Рассмотрим два контура 1 и 2, расположенные близко друг к другу (рис. 6.6). Если в контуре 1 течет ток силы I1, то он создает через контур 2 полный магнитный поток

пропорциональный I1. Поле, создающее этот поток, изображено на рисунке сплошными линиями. При изменении тока I1 в контуре 2 индуцируется ЭДС

i1 ddtΨ1 .

Контуры 1, 2 называются связанными, а явление возникновения ЭДС в одном из контуров при изменении силы тока в другом называется взаимной индук-

цией.

Коэффициенты пропорциональности L12 и L21 называются взаимной индуктивностью контуров. Их величина зависит от формы, размеров и взаимного расположения контуров, а также от магнитной проницаемости μ окружающей среды. В отсутствии ферромагнетиков μ = const и L12 = L21.

6.4. Энергия магнитного поля

Вернемся к схеме, изображенной на рисунке 6.4. При подключенном источнике ток, текущий в катушке индуктивности, создает внутри нее магнитное поле. Если с помощью ключа отсоединить источник, оставив цепь замкнутой, сила тока, как мы видели, будет убывать по экспоненте. При этом, за малый промежуток времени dt будет совершена работа dA = εSIdt, где εS - ЭДС самоиндукции. Подставив сюда ее выражение (6.4), получим dA = - LI dI. Чтобы найти работу, совершаемую за время практически полного исчезновения тока (и магнитного поля в катушке), проинтегрируем это соотношение по току от его начального значения до нуля

59

Эта работа идет на нагревание проводов и резистора R, и совершается, очевидно, за счет энергии магнитного поля, существовавшего в катушке. Можно, таким образом, заключить, что катушка, по которой течет ток I, обладает энергией

Поскольку носителем этой энергии является магнитное поле, имеет смысл выразить ее через параметры, характеризующие поле, т.е. В и Н. Поскольку

где учтено, что B = μ0μH.

Полученные выражения применимы и в случае неоднородного поля. Формулы (6.12) дают значение плотности энергии в данной точке пространства. Энергия, заключенная в конечном объеме V, может быть вычислена по следующей формуле

6.5. Уравнения Максвелла для электромагнитного поля

Теория электромагнитного поля была разработана британским физиком Джеймсом Максвеллом в 1865 г. Это поле представляет собой совокупность электрического и магнитного полей, которые могут, при определённых условиях, порождать друг друга.

Как показал Фарадей, индукционный ток в проводящем замкнутом контуре возникает при любом изменении магнитного потока, пронизывающего этот контур. Допустим, что контур неподвижен, а меняется индукция магнитного поля. Движение зарядов в замкнутом проводнике подразумевает суще-

60

ствование в нем электрического поля, циркуляция которого не равна нулю, то есть вихревого электрического поля.

Максвелл предположил, что любое переменное магнитное поле порождает в окружающем пространстве вихревое электрическое поле, независимо от

наличия в нем носителей тока. Обозначим напряженность этого поля символом

Ев . Работа A перемещения заряда q по замкнутому контуру L будет равна

напряженность вихревого и электростатического полей, поскольку для электростатического поля циркуляция равна нулю. Интеграл в правой части берется по произвольной поверхности, опирающейся на контур L. Переход к частной про-

изводной связан с тем, что B зависит в общем случае еще и от координат. Выражение (6.14) дает, таким образом, полное описание явления элек-

тромагнитной индукции. Оно показывает, что переменное магнитное поле приводит к появлению вихревого электрического поля, величина которого (т.е.

циркуляция вектора E ) определяется скоростью изменения магнитного потока. Это уравнение является одним из основных в теории электромагнитного поля Максвелла, устанавливающей связь между электрическими и магнитными явлениями.

Развивая свою теорию, Максвелл предположил, что существует и обратное явление: переменное электрическое поле должно порождать вихревое магнитное поле. Поскольку магнитные поля создаются токами, Максвелл назвал переменное электрическое поле током смещения. Этот ток, в отличие от тока проводимости, не связан с движением зарядов.

Рассмотрим цепь, содержащую источник переменного тока и конденсатор

без диэлектрика (рис. 6.7). При зарядке и разрядке конденсатора в цепи суще-

ствует ток проводимости, плотность которого обозначим j .