Центр дистанционного
обучения
ФИЗИКА
Электромагнитные колебания. Колебательный контур
ФИО преподавателя: Экономов Николай Андреевич
mail: economov@list .ru
Online- edu.mirea.ru
online.mirea
.ru
Центр дистанционного
обучения
online.mirea
.ru
Центр дистанционного
обучения
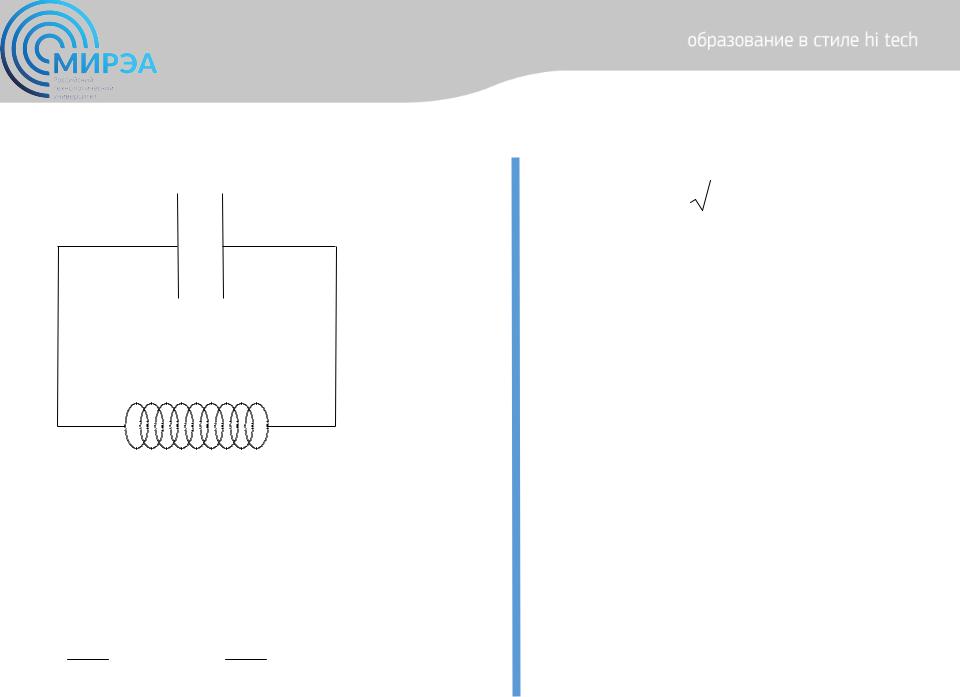
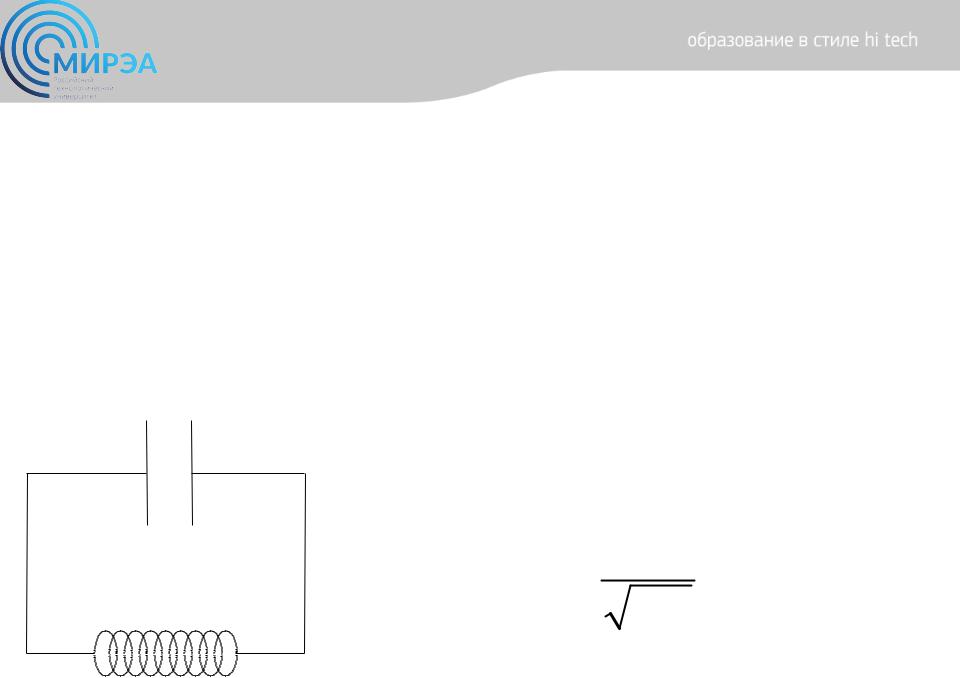
Электромагнитные колебания. Колебательный контур
С
Рис. 1 |
|
L |
|
|
Wполная WC WL const |
(1.7) |
|||
q2 |
LI 2 |
q02 |
LI02 |
(1.8) |
2C |
2 |
2C |
2 |
|
T 2 |
|
|
|
|
(1.1) |
||||
|
LC |
||||||||
q q0 cos( t) |
(1.2) |
||||||||
U |
q |
|
q0 |
cos( t) |
(1.3) |
||||
|
|
|
|||||||
|
C |
C |
|
||||||
U U0 cos( t) |
(1.4) |
||||||||
U0 |
q0 |
|
|
|
|
|
(1.5) |
||
C |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
I q q0 sin( t) |
(1.6) |
||||||||
online.mirea
.ru
Центр дистанционного
обучения
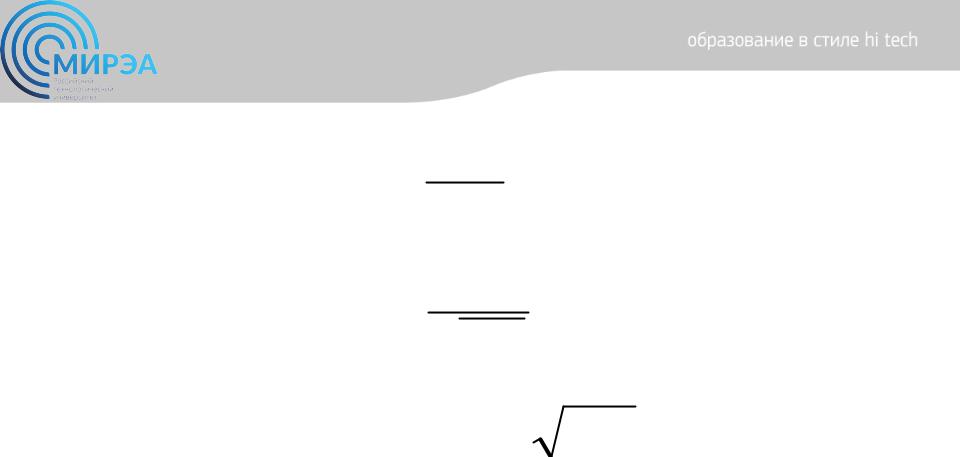
q LCq 0
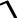
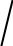LC1
T 2 2 LC
(1.13)
(1.14)
(1.15)
online.mirea
.ru
Центр дистанционного
обучения
Задача 1. Амплитуда силы тока в контуре 1,4 мА, а амплитуда напряжения 280 В. Найти силу тока и напряжение в тот момент, когда энергия магнитного поля катушки равна энергии электричес- кого поля конденсатора.
CU 2 |
|
LI |
2 |
CU 2 |
|
LI 2 |
|||||||
0 |
|
0 |
|
2 |
2 |
||||||||
2 |
|
|
|
|
|
|
2 |
|
|
|
|||
CU 2 |
|
LI 2 |
|
|
|
|
|||||||
|
2 |
|
|
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
CU 2 |
2 |
CU 2 |
|
|
|
||||||||
0 |
|
2 |
|
|
|
||||||||
2 |
U |
|
|
|
|
|
|
|
|
||||
U |
0 |
|
|
200B |
|
|
|
||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
||
(2.1)
(2.2)
(2.3)
(2.4)
LI |
2 |
2 |
LI 2 |
0 |
2 |
||
2 |
|
|
|
I I02 1мА
(2.5)
(2.6)
online.mirea
.ru
Центр дистанционного
обучения
Задача 2. Максимальное напряжение в колебательном контуре, состоящем из катушки индуктивностью
L 5мкГн и конденсатора ёмкостью C 13330пФ, равноU0 1,2В. Сопротивление ничтожно мало. Определить: а) действующее значение тока в контуре; б) максимальное значение магнитного потока через
один виток, если число витков катушки N = 28.
С
|
|
q q0 cos t |
(3.1) |
|
|
|
2 |
1 |
(3.2) |
|
|
T |
LC |
|
|
|
|
||
|
Рис. 2 |
q CU |
0 |
(3.3) |
L |
0 |
online.mirea |
||
|
|
|
.ru |
|
Центр дистанционного
обучения
I q q0 sin t
I0 q0 CULC0 
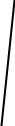CLU0
I Д I02 
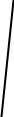2CLU0
(3.4)
(3.5)
(3.6)
|
|
|
|
I Д |
13330 10 12 |
1,2 44 10 3А |
|
|
2 5 10 6 |
|
|
online.mirea
.ru
|
|
|
|
|
|
|
|
|
|
|
Центр дистанционного |
|||||
|
|
|
LI0 |
|
обучения |
|
||||||||||
|
|
|
|
|
|
|
|
|
(3.7) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
N |
|
|
|
|
|
|
(3.8) |
|||||
|
|
|
|
|
|
|
LI0 |
|
|
|
|
|
|
|
|
(3.9) |
|
|
|
|
N |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
L |
|
C |
U0 |
|
|
LC |
|
U0 |
(3.10) |
||||
|
|
|
N |
|
L |
N |
|
|||||||||
|
|
|
|
|
|
|||||||||||
|
|
5 10 6 13330 10 12 |
|
|
1,2 1,1 10 8Вб |
|||||||||||
|
28 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
.ru |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
online.mirea |
Центр дистанционного
обучения
Задача 3. Конденсатор колебательного контура приемника
имеет ёмкость C. На какую длину волны резонирует |
|
||||||
контур приёмника, если отношение максимальных |
|
||||||
значений напряжения на контуре и тока в катушке |
|
||||||
контура при резонансе равно m/n. |
|
|
|
||||
CU02 |
|
LI02 |
(4.1) 2 c |
m |
C |
(4.5) |
|
2 |
2 |
|
n |
||||
|
|
(4.2) |
|
|
|||
|
|
|
|
||||
cT c2 LC |
|
|
|
||||
U0 |
|
|
|
|
|
m |
|
|
L |
|
|
(4.3) |
|||
I0 |
C |
|
n |
||||
|
|
|
|
|
|||
|
m |
|
(4.4) |
|
|
|
|||
L n C |
||||
|
||||
online.mirea
.ru
Центр дистанционного
обучения
Задача 4. Длина воздушной линии передачи 300 км. Частота напряжения 50 Гц. Найти сдвиг по фазе в начале и в конце линии.
UU0 sin t
t - фаза
2 1
2 t21 t1
(5.1
)
(5.2
)
(5.3
)
(5.4
)(5.5
)
online.mirea
.ru