2-й семестр / Лекция 10

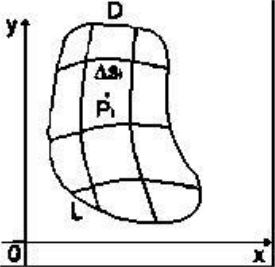
Двойной интеграл

К понятию определенного интеграла приводит, в частности, задача о вычислении площади криволинейной трапеции. Задача о вычислении объема «криволинейного параллелепипеда» приводит к понятию двойного интеграла. Приведем точные определения.

Рассмотрим в плоскости ограниченную замкнутую область с границей . Разобьем эту область какими-нибудь линиями на частей 1, 2, . . . , (теми же символами 1, 2, . . . , будем обозначать и площади соответствующих частей). Наибольшие расстояния между точками в каждой из этих

=1

называется интегральной суммой для функции (, ) в области .

1

Замечание. С геометрической точки зрения (при (, ) ≥ 0) интегральная сумма представляет собой сумму объемов цилиндров с основаниями и высотами ( ).

Определение 2. Если существует предел интегральных сумм при → ∞ и → 0, не зависящий ни от способа разбиения области на части, ни от выбора точек в них, то он называется

двойным интегралом от функции (, ) по области и обозначается

для разбиения

В этом случае говорят, что функция (, ) интегрируема в области .

Теорема. Если функция непрерывна в ограниченной замкнутой области , то она интегрируема в этой

области.

2

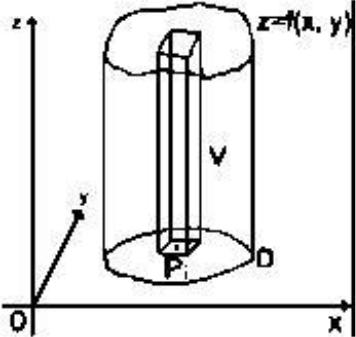
Рассмотрим тело , ограниченное частью поверхности, задаваемой графиком функции = (, ),

проекцией этого графика на плоскость и боковой цилиндрической поверхностью, полученной из вертикальных образующих, соединяющих точки границы поверхности с их проекциями (это то тело,

которое часто называют «цилиндрическим телом»).

Объем этого тела есть, очевидно, предел суммы объемов цилиндров, основаниями которых являются части

области , а высотами – отрезки длиной ( ), где точки принадлежат . Другими словами,

переходя к пределу при → 0, получим, что

для разбиения

о есть двойной интеграл представляет собой объем тела .

3

Свойства двойных интегралов

Свойства двойного интеграла непосредственно вытекают из его определения или из свойство пределов :

1. Линейность интеграла Если функция (, ) интегрируема в , то функция (, ), где = ,

тоже интегрируема в этой области и при этом

(, ) = (, )

2. Линейность интеграла Если в области интегрируемы функции (, ) и (, ),

то в этой области интегрируемы и функции (, ) ± (, ), и при этом

((, ) ± (, )) = (, ) ± (, )

4

3. Монотонность интеграла. Если для интегрируемых в области функций (, ) и (, ) выполняется неравенство (, ) ≤ (, ) для всех (, ) из , то

(, ) ≤ (, )

4. Аддитивность интеграла. Если область разбита на две области 1 и 2 без общих внутренних точек

ифункция (, ) интегрируема в области , то

(, ) = (, ) + (, )

1 2

Доказательство: интегральную сумму по области можно представить в виде:

где разбиение области проведено так, что граница между 1 и 2 состоит из границ частей разбиения.

Переходя затем к пределу при → 0, получим требуемое равенство.

5

5.Если функция (, ) интегрируема в области , то функция | (, )| также интегрируема в и имеет место неравенство

| (, ) | ≤ | (, )|

Доказательство: учитывая, что

|∑ ( ) | ≤ ∑| ( )| ,

откуда с помощью предельного перехода при → 0 получаем нужное неравенство

6.Площадь области можно найти по формуле

= , где – площадь области .

Доказательство: этого утверждения получим, подставляя в интегральную сумму (, ) ≡ 1.

7.(Теорема об оценки интеграла) Если интегрируемая в области функция (, ) удовлетворяет неравенству ≤ (, ) ≤ , то

6

≤ (, ) < .

Доказательство: проводится предельным переходом из очевидного неравенства

Геометрический смысл теоремы о среднем.

Теорема о среднем имеет простой геометрический смысл: существует точка 0 = (0, 0) такая, что объем «цилиндрического тела » равна объему цилиндра с площадью основания

= и имеющего высоту ( 0)

7

Вычисление двойного интеграла

Определение.Область называется простой в направлении оси , если всякая прямая параллельная оси, проходящая внутри отрезка [, ], пересекает границу области только в двух точках.

8

Рассмотрим область , ограниченную графиками непрерывных функций = 1( ), = 2( ) (1( ) ≤ 2( )), определенных на отрезке [, ] и прямыми = и =

Теорема. Если функция (, ) непрерывна в простой в направлении оси области , то

Вэтом случае двойной интеграл вычисляется по формуле

2( )

т. е. сводится к последовательному вычислению определенных интегралов, или, как говорят, к повторному

интегрированию.

Традиционно выражение справа записывают так

Если область можно разбить линиями на конечное число подобластей, каждая из которых является простой, то используя свойство 4 двойного интеграла, мы снова сводим его вычисление к повторному интегрированию.

9

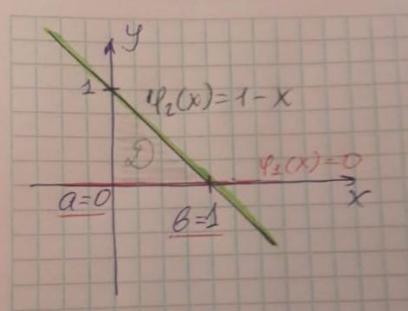
Пример 1.

Вычислим двойной интеграл от функции ( , ) = + по области, представляющей собой треугольник с вершинами в точках (0,0), (0,1) и (1,0)

Здесь = 0, = 1, 1( ) = 0, 2( ) = 1 − .

Теорема. Если функция ( , ) непрерывна в простой в направлении оси области , то

Вэтом случае двойной интеграл вычисляется по формуле

2( )

т. е. сводится к последовательному вычислению определенных интегралов, или, как говорят, к повторному

интегрированию.

10