
2-й семестр / Лекция 07
.pdf
ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Определенные интегралы имеют многочисленные приложения в самых разнообразных задачах. Здесь мы ограничимся рассмотрением некоторых геометрических приложений.
На предыдущей лекции уже были рассмотрены некоторые геометрические приложения определенного интеграла. Мы напомним эти приложения и рассмотрим новые.
1.Площадь плоской области
a)Вычисление площади в прямоугольных координатах
Найти площадь плоской области, ограниченной двумя непрерывными линиями – графиками функций ( ) и ( ) (см. рис.).
Такая площадь находится по следующей формуле:
= ∫ [ ( )− ( )] ,
где – площадь криволинейной плоской области, ограниченной графиками функций у = ( ), у = ( ) таких, что ( ) ≥ ( ) на [a, b], и по бокам
- отрезками прямых = и = .
б) Площадь криволинейного сектора в полярных координатах
Пусть кривая задана в полярных координатах уравнением ( ),, причем функция ( ) непрерывна и неотрицательна на отрезке [ , ]. Плоскую фигуру, ограниченную дугой AB этой кривой и двумя лучами, составляющими с полярной осью углы и ( , ),
|
|
i |
|
B |
|
|
|
A |
|
|
|
|
|
|
0 |
|
C |
называют криволинейным сектором (см. рис.).

Тогда площадь криволинейного сектора вычисляется по формуле:
= ∫ ( ) .
Обоснование этой формулы было приведено в предыдущей лекции.
2. Нахождение объема тела, используя площади его поперечных сечений
Пусть имеется тело объема V. Пусть дана площадь любого поперечного сечения тела в виде непрерывной функции Q = Q(x).
Тогда объем данного тела может быть найден по формуле:
= ∫ ( ) ,
где ( ) – площадь поперечного сечения тела в точке .
Обоснование этой формулы было приведено в предыдущей лекции.
Объем тела вращения
Пусть функция f (x) непрерывна и неотрицательна на отрезке [a,b]. Найдем объем тела, образованного вращением криволинейной трапеции,
ограниченной кривой y f (x) и прямыми y a, |
y b, x 0, вокруг оси x. |
|||||||
В данном случае поперечное сечение в точке |
представляет собой круг |
|||||||
радиуса |
|
, площадь которого равна |
|
. |
Применяя к нахождению |
|||
объема этого( )тела общую формулу, полученную( )выше, получаем: |
= |
|||||||
Объем, |
тела |
вращения, образованного вращением графика функции |
||||||
], |
вокруг оси OX находится по формуле: |
|||||||
( ) ≥ |
[ , |
= |
( ) . |
|
|
|
||
|
|
|
|
|
|
|
||
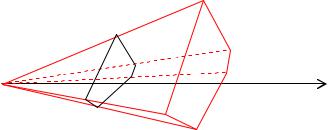
Пример: Найти объем произвольной пирамиды с высотой Н и площадью основания S.
Решение. При пересечении пирамиды плоскостями, перпендикулярными высоте, в сечении получаем фигуры, подобные основанию. Коэффициент подобия этих фигур равен отношению x/H, где х – расстояние от плоскости сечения до вершины пирамиды.
Из геометрии известно, что отношение площадей подобных фигур равно коэффициенту подобия в квадрате, т.е.
Q |
|
x 2 |
|
|
|
|
|
S |
|
||
H |
|||
Отсюда получаем функцию площадей сечений: Q(x) |
S |
x2. |
||||||||||
H2 |
||||||||||||
H |
|
|
|
|
|
|
|
|
|
|
||
S |
|
|
Sx |
3 |
|
H |
1 |
|
|
|
||
Находим объем пирамиды: V |
|
x2dx |
|
|
|
SH |
|
|||||
|
|
|
|
|||||||||
H |
2 |
3H |
2 |
3 |
|
|||||||
0 |
|
|
|
|
0 |
|
|
|
||||
Рассмотрим теперь другие приложения определенного интеграла.
3. Нахождение длины дуги кривой
a) Кривая задана в явной форме
|
Пусть требуется определить длину дуги AB кривой y f (x), a x b, |
|||||
где |
f C1[a,b]. |
Разобьем отрезок |
[a,b] |
на |
n частей |
точками |
a x0 x1 ... xn 1 |
xn b. Тогда длина |
L дуги AB приближенно равна |
||||
длине ломаной, вписанной в данную кривую: |
|
|
|
|||
|
|
n 1 |
|
|
|
|
|
|
L li , |
|
|
(1) |
|
|
|
i 0 |
|
|
|
|
где li – длина хорды (одного звена ломаной) |
MiMi 1 (рис. 6). Здесь точка |
|||||
Mi |
имеет координаты Mi (xi, f (xi )). Естественно длиной L дуги AB считать |
|||||
предел длин ломаных, вписанных в эту кривую, при d 0, где |
|
|||||
|
|
|
|
n 1 |
|
|
|
|
d max (xi 1 xi ):L lim li |
, |
(2) |
||
|
|
0 i n 1 |
d 0 i 0 |
|
|
|
если, конечно, этот предел существует.

y |
|
|
|
|
M n |
|
M 1 |
|
M 2 |
M n 1 |
|
|
|
|
|
|
|
|
M 0 |
|
|
|
|
|
|
|
x2 |
|
x |
0 |
a x0 |
x1 |
xn 1 |
xn b |
По теореме Пифагора имеем ( li )2 (xi 1 xi )2 (yi 1 yi )2 . Но в силу теоремы Лагранжа получим
|
|
|
|
|
yi 1 yi f (xi 1) f (xi ) f ( i )(xi 1 xi ), |
|
|
||||||||||||||||||||||||||
где i (xi |
,xi 1). Тогда li |
|
1 ( f ( i ))2 |
|
|
xi |
, |
|
xi |
xi 1 |
|
xi . |
|
||||||||||||||||||||
Если подставить эти равенства в правую часть соотношения (21), то |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получим |
интегральную |
сумму функции |
|
|
|
|
|
|
2 |
|
на |
отрезке [a,b]. |
|||||||||||||||||||||
|
1 f |
(x) |
|||||||||||||||||||||||||||||||
Функция |
|
|
|
|
2 |
|
непрерывна на отрезке [a,b], поэтому предел (22) |
||||||||||||||||||||||||||
|
1 f (x) |
||||||||||||||||||||||||||||||||
этой суммы существует и равен определенному интегралу |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
=длину |
полукубической+ ( ( )) |
|
параболы. |
|
(3) |
|||||||||||||||||||||
Пример. Вычислить |
∫ |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
y x 2 , если 0 x 5. |
|
|
|
|
|
|
|
|
|
||||||||||||||||
Решение. Общее |
уравнение |
полукубической |
параболы имеет |
вид |
|||||||||||||||||||||||||||||
a2x3 y2 |
0. В данном случае нужно найти длину дуги верхней ветви. Из |
||||||||||||||||||||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
3 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
уравнения |
|
y x |
2 находим: |
|
y |
|
|
x 2 . |
Следовательно, |
|
по |
формуле |
(23) |
||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
9x |
|
|
|
|
8 |
|
9x |
|
335 |
|
|
|||||||||||||
получим |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||||||||||
L 1 (y ) |
dx |
1 |
|
|
|
|
dx |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
4 |
|
|
|
|
4 |
|
|
|
27 |
|
|||||||||||||||||||||||
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
27 |
|
|
|
|
|
0 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) Кривая задана в параметрической форме |
|
|
||||||||||||||||||||||||||||
Рассмотрим гладкую кривую L, заданную параметрически: x=x(t); y=y(t); z=z(t), где t [α,β], значению α отвечает точка А – начало кривой, а значению β – точка B – конец кривой. Разобьем кривую на «n» частей точками A=M0 , M1,..., Mn=B. Точки Мi соединим ломаной, которая будет вписана в кривую L.
Вычислим периметр ломаной M0 , M1,..., Mn. Если каждой точке деления Mi отвечает значение параметра ti, то длина звеньев ломаной определится из теоремы Пифагора:

| |
=x( |
| |
) -∆ |
+∆ i |
+∆i |
|
|
|
|
|
|
|
∆ |
|
|
= |
|
|
, где, по теореме Лагранжа о среднем, |
||||||
|
|
x( |
)=x′(t′) t |
|
|
|
|
|
|
|||
=y( |
|
) - y( |
)=y′′(t′′′i′′) ti |
|
|
|
|
|
|
|||
∆ |
=z( |
|
) - z( |
)=z(ti |
) ti , причем ti = ti+1 - ti |
|
|
|
|
|||
∆ |
|
|
|
|
|
|||||||
При n , ti 0, длина кривой L будет равна: |
|
|
|
|
||||||||
|
L = lim → |
∑ | |
|
| = lim → |
∑ |
|
|
|
|
= |
||
|
∆ |
+∆ |
ti |
+∆ |
||||||||
|
|
( )+ ( |
)+ |
( |
) |
|
||||||
|
|
|
lim → |
∑ |
|
|
|
|||||
Таким образом, получаем:
Длина кривой, заданной параметрически, находится по формуле:
L = ∫ |
( )+ ( )+ ( ) |
Пример. Вычислить длину дуги астроиды:
x = acos3t, y = asin3t, t [0,2π]
Применяя формулу, находим:
L = 4∫ / |
9 |
cos ( ) sin= |
(6) +9 |
sin=(6) cos ( ) |
= |
12 |
∫ / |
|
| |
/ |
|
в) Плоская кривая задана в полярных координатах
Предположим, что кривая лежит в плоскости XOY и задана в параметрическом виде x=x(t); y=y(t); где t [α,β]. Тогда полученная формула для ее длины принимает вид:
|
|
|
L = ∫ |
( ) + ( ) . |
|
Перейдем в этой формуле к полярным координатам по формулам:
x rcos ,
y rsin ,
и найдем dx rcos d (r cos rsin )d , dy rsin d (r sin rcos )d .
Подставив найденные дифференциалы в формулу длины кривой, получим:
Длина дуги в полярных координатах находится по формуле:
L = ∫ ( )+ ′ ( )
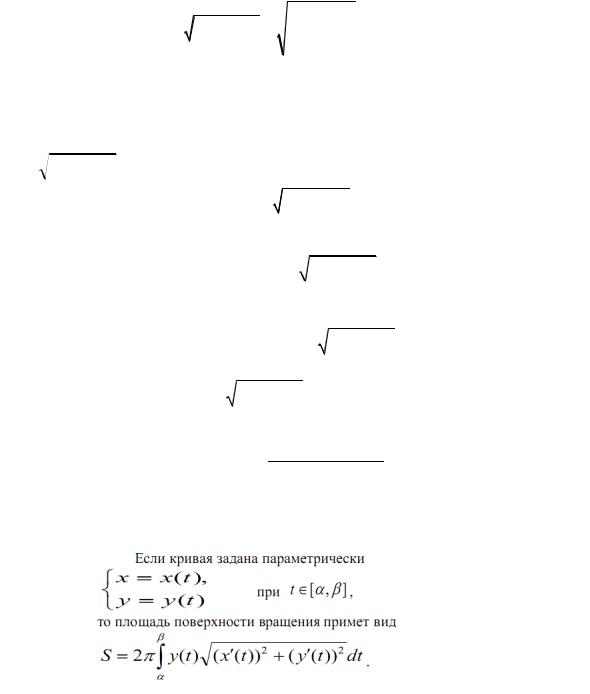
4. Площадь поверхности тела вращения
Площадью поверхности вращения кривой АВ вокруг данной оси называют предел, к которому стремятся площади поверхностей вращения ломаных, вписанных в кривую АВ, при стремлении к нулю наибольших из длин звеньев этих ломаных.
Разобьем дугу АВ на n частей точками M0, M1, M2, … , Mn. Координаты вершин полученной ломаной имеют координаты xi и yi. При вращении ломаной вокруг оси получим поверхность, состоящую из боковых поверхностей усеченных конусов, площадь которых равна Si. Эта площадь может быть найдена по формуле:
|
|
|
|
S 2 |
yi 1 yi |
l |
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
i |
|
|
|
2 |
|
|
|
i |
|
|
|
Здесь li – длина каждой хорды. |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
1 |
yi |
2 |
|
||||
|
|
l x2 |
y2 |
x |
|||||||||||
|
|
x |
|
||||||||||||
|
|
|
i |
i |
i |
|
|
|
i |
||||||
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
||
Применяем теорему Лагранжа к отношению |
yi |
|
. Получаем: |
||||||||||||
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
xi |
|
|
||
|
yi |
|
f (xi ) f (xi 1) |
f ( i ), |
|
|
|
xi 1 xi |
|||||||
|
xi |
|
|
|
|
||||||||||
|
|
xi |
xi 1 |
|
|
|
|
|
|
|
|
||||
Тогда li 
 1 f 2( i) xi и, следовательно,
1 f 2( i) xi и, следовательно,
|
yi 1 yi |
|
|
|
|
|
1 f |
2 |
|
||
Si 2 |
|
( i) xi |
|||
|
|||||
2 |
|
|
|
|
|
Площадь поверхности, описанной ломаной равна:
n
Sn f (xi 1) f (xi)  1 f 2( i) xi
1 f 2( i) xi
i 1
Эта сумма не является интегральной, но можно показать, что
|
|
|
|
n |
f (x |
) f (x ) |
|
|
|
|
|
|||||
|
|
|
|
1 f 2( |
|
|
|
|||||||||
S |
lim |
|
|
) x |
|
|||||||||||
max x 0 |
|
|
|
|
i 1 |
|
i |
|
i |
|
i |
|
||||
|
i |
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
2f ( |
) |
1 f 2( |
) x |
|
|
|
|||||||
max x 0 |
|
|
i |
|
|
|
i |
|
|
i |
|
|
|
|||
i |
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Получаем формулу для вычисления площади поверхности тела вращения
= |
( ) +( ( )) |
Дополнение.
