Добавил:

Rumpelstilzchen Rumpelstilzchen2018@yandex.ru Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

МИРЭА - Российский технологический университет

Предмет:

Линейная алгебра

Файл:

Лекция 15

.pdf

Скачиваний:

Добавлен:

02.06.2020

Размер:

849 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Построение ортонормированного базиса из собственных

векторов для симметричного линейного оператора

На прошлой лекции мы изучили ортогональные и симметричные операторы в евклидовом пространстве.

Мы выяснили, что

Ортогональная матрица может не иметь действительных собственных значений.

Симметрическая матрица ВСЕГДА имеет действительное собственное значение.

Все собственные значения симметрической матрицы – действительные числа.

Собственные векторы симметрической матрицы, принадлежащие различным собственным значениям, ортогональны.

Для любой симметрической вещественной матрицы A существует ортогональная матрица U, такая, что матрица U-1AU – диагональная матрица.

Алгоритм нахождения ортонормированного базиса из собственных векторов симметрической матрицы:

I. Найти характеристические числа i заданной симметрической матрицы.

II. Если i - простой корень характеристического уравнения, то ему отвечает с точностью до множителя один собственный вектор. Нормируем его и получаем единичный вектор.

Если i - корень кратности k , то ему отвечают k линейно независимых собственных векторов. В этом случае их необходимо отогонализировать и подвергнуть нормировке - получаем k линейно независимых ортонормированных вектора,

отвечающих собственному значению i . Так как собственные векторы, отвечающие различным характеристическим числам, ортогональны, то, собирая их вместе,

получаем ортонормированный базис из собственных векторов.

Пример 1. Привести к диагональному виду с помощью ортогональной матрицы

1		2	2

симметрическую матрицу A	2	1	2	. Указать ортонормированный базис.
	2	2	1
	2	2	1

Решение.

На первом шаге необходимо найти собственные значения данного линейного оператора.

Составим характеристическое уравнение данного преобразования: Ae E 0 .

					2		2		II III			5	5	5
			1		2		2		II III			5	5	5

Ae E			2		1		2					2	1	2
			2		2		1					2	2	1
		1			1					1	1		1
	1	1			1					1	1		1
(5 )	2	1			2		2I	(5 )		0	1		0	(5 )(1 )2	0
	2	2		1		2II				0	0		1

		1, алг кратность 2
Корни уравнения	1		- собственные значения линейного
	2	5, алг кратность 1

ˆ
оператора A .
На втором шаге найдем собственные векторы, относящиеся к каждому
собственному значению.
1. 1 1	. Решим матричное уравнение (Ae 1 E)X 0 .
	2 2			2 x			0
						1
( Ae E)	X	2 2		2		x2		0
		2 2		2				0
		2 2		2	x3			0
											1				1

Решением	является			вектор			U		С1			1	С2		0	, C1,C2	0 , базис
								1
												0			1
												0			1
пространства решений образуют векторы u ( 1;1;0)T , u														2	( 1;0;1)T
								1						2
2. 2 5 . Решим матричное уравнение (Ae 5 E)X 0 .
		4		2		2 x				0
								1
( Ae 5E) X			2	4 2			x2				0
			2	2 4 x							0
								3

					1
		векторы U 2		С3		C3 0 ,
Решением являются		векторы U 2		С3	1 ,	C3 0 ,	базисом	пространства

					1
решений является вектор u		(1;1;1)T .
	3
Вектор	u3 (1;1;1)	ортогонален векторам				u1 ( 1;1;0) и		u2 ( 1;0;1) ,
поскольку они относятся к различным собственным значениям.
Ортогонализируем векторы u1 ( 1;1;0)					и u2	( 1;0;1) .
Пусть	f1 u1
f2 u2 f1 . Выберем			таким	образом,		чтобы	векторы	f1, f2 были

ортогональны, то есть ( f1, f2 ) 0 ( f1, f2 ) ( f1, u2 f1) ( f1, u2 ) ( f1, f1) 0

( f1,u2 ) (u1,u2 ) 1 ( f1, f1) (u1,u1) 2

f		u		1	f		1		( 1;1;0) ( 1;0;1) (													1	;		1		;1)
f		u			f				( 1;1;0) ( 1;0;1) (														;				;1)
	2		2	2	1		2															2			2
Теперь векторы						f1, f2 , u3							ортогональны.

																3
						f						2 ,
Нормируем их.													f	2				,	u	3 .
Нормируем их.													f					,	u	3 .
						1										2			3
								1			1					2																1			1		1

					h (					;			;0)			h			(		1	;		1		;		2	)		h (			;		;		)
Векторы					h (					;			;0)		,	h			(			;				;			)	,	h (			;		;		)
Векторы					1		2					2			,		2				6		6				3			,	3		3		3		3
							2					2									6		6				3						3		3		3

составляют искомый ортономированный базис.

	1		1	1


	2	6		3
	1		1	1
Ортогональная матрица U

	2	6		3
	2	6		3
	0	2		1


		3		3
		3		3

Матрица обратная к U совпадает с UТ, то есть

	1		1
					0

		2	2
		2	2
U 1		1		1	2


		6	6		3
		6	6		3
		1	1		1

		3	3		3
		3	3		3

f (x1, x2,..., xn ) с

f (x1, x2,..., xn ) .

f (x1, x2,..., xn ) ,

преобразование

	ˆ
Матрица оператора A в базисе из собственных векторов имеет вид
1		0	0

Ah U 1AeU	0	1	0
	0	0	5
	0	0	5

ОРТОГОНАЛЬНОЕ ПРЕОБРАЗОВАНИЕ, ПРИВОДЯЩЕЕ КВАДРАТИЧНУЮ ФОРМУ К КАНОНИЧЕСКОМУ ВИДУ

Ранее мы говорили о методе Лагранжа приведения квадратичной формы к каноническому виду – методе выделения полных квадратов. В результате получалось некоторое линейное преобразование, в общем случае не однозначно определенное, но

среди всех таких матриц всегда можно выбрать ортогональную.

С другой стороны, рассмотренная нами выше формула приведения матрицы к диагональному виду с помощью ортогонального преобразования D = U-1AU= UTAU ( в

силу U-1= UT) аналогична преобразованию симметрической матрицы A квадратичной формы с линейным преобразованием неизвестных U. Поскольку диагональную матрицу имеет квадратичная форма, приведенная к каноническому виду, получаем

следующую теорему.

Теорема 1. Для каждой действительной квадратичной формы

заданной в евклидовом пространстве, можно указать ортогональное неизвестных, приводящее ее к каноническому виду.

Геометрически такой выбор матрицы означает переход к новой декартовой системе координат, определяемой ортонормированным базисом собственных векторов матрицы A. Новые оси координат называют в этом случае главными осями матрицы A

и соответствующей квадратичной формы Теорема 1 называется

теоремой о приведении действительной квадратичной формы к главным осям.

Теорема 2. Каково бы ни было ортогональное преобразование, приводящее к

каноническому виду квадратичную форму матрицей A,

коэффициентами этого канонического вида будут характеристические корни матрицы

A, взятые с их кратностями.

В матричной формулировке теорема 2 может быть переписана в виде

Теорема 3. Какова бы ни была ортогональная матрица, приводящая к диагональному виду симметрическую матрицу A, на главной диагонали полученной

f (x1, x2,..., xn )

диагональной матрицы будут стоять характеристические корни матрицы A, взятые с их кратностями.

Приведению квадратичной формы к главным осям можно

придать следующую геометрическую формулировку: в евклидовом пространстве уравнение f (x1, x2,..., xn ) С определяет некоторую поверхность второго порядка.

Ортогональное преобразование X Ce f Y , приводящее форму к каноническому

виду означает поворот декартовых осей, осуществляющий преобразование уравнения

поверхности второго порядка	к каноническому виду, по которому легко узнать тип
данной поверхности.
Пример 2. Найти ортогональное преобразование, приводящее к каноническому
виду квадратичную форму f (x , x ) 17x2			12x x			8x2
1	2	1		1	2	2
Решение.
		17		6
Матрица квадратичной формы:		A
			6
			6	8

Найдем корни характеристического уравнения							Ae E	0 .
Найдем корни характеристического уравнения							Ae E	0 .
	Ae E	17	6						20
		17	6						20
			8	2	25 100	( 20)( 5)		0 1		-
		6	8					2	5

собственные значения.

Найдем собственные векторы, относящиеся к каждому собственному значению:

1 20 . Решим матричное уравнение (Ae 20Е)X 0 .
3	6		x1			0	3	6			1 2
						,		12
6	12		x			0	6	12				0 0
			2
Решением		являются				векторы		U				2	C 0	,		базисом пространства
Решением		являются				векторы		U	1	С		,	C 0	,		базисом пространства
									1		1		1
												1
решений является вектор u1 (2;1)T .								Нормируем его:					h1 (		2		;	1	)

															5			5
															5			5
2 5 . Решим матричное уравнение (Ae 5Е)X 0 .
12	6	x1		0	,	12	6	2			1
					,
									0
6	3	x2		0		6	3		0		0

Решением являются векторы	U		С		1	,	C		0	, базисом пространства
		2		2				2
					2

решений является вектор u2 ( 1;2)T . Нормируем его:															h2	(	1	;	2	)

																	5		5
																	5		5
		2			1


		5			5
U		5			5
		1			2


		5
		5				5
												2	1
															y


											X UY	5		5
Искомое преобразование											X UY	5		5	1
Искомое преобразование												1	2
												1	2		y2
															y2
												5
												5		5
x		2		y			1	y
x				y				y	2
1		5	1				5		2
		5					5
		1					2
x		1		y			2	y
x	2			y				y		2
	2	5	1				5			2
		5					5

Канонический вид квадратичной формы:				f 20 y2			5y2
						1	2
Пример 3. Найти ортогональное преобразование, приводящее к каноническому
виду квадратичную форму f (x , x , x ) 2x2				x2	x2		4x x	4x x	2x x
1	2	3	1	2		3	1 2	1 3	2	3
Решение.
		2		2	2

Матрица квадратичной формы		A	2	1	1
			2	1	1
			2	1	1

Составим характеристическое уравнение данного преобразования: Ae E 0 .

		2	2			2
		2	2			2
	A E	2	1			1	(2 )2 (4 ) 0
	A E	2	1			1	(2 )2 (4 ) 0
	e
		2	1		1
Корни уравнения				2		- собственные значения.
Корни уравнения			1			- собственные значения.
			2	4

На втором шаге найдем собственные векторы, относящиеся к каждому собственному значению.

1. 1 2 , решая матричное уравнение (Ae 2 E)X 0 ,

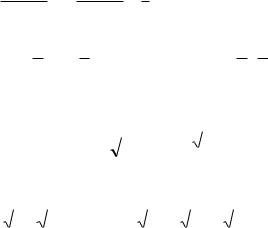
				4			2	2 x1		0

( Ae		2E) X			2		1	1	x2	0
					2					0
					2		1 1 x3			0
4		2	2		2		1 1

	2	1	1			0	0 0
	2	1 1				0	0 0

	1					1
Решением является вектор U 1					С2
Решением является вектор U 1	С1	2			С2		0	, C1,C2	0 , базис пространства
		0					2
		0					2
решений образуют векторы u ( 1;2;0)T ,		u		2	(1;0;2)T . Ортогонализируем их.
1				2
Пусть f1 u1
f2 u2 f1 . Выберем	таким		образом,					чтобы	векторы f1, f2 были

ортогональны, то есть ( f1, f2 ) 0 ( f1, f2 ) ( f1, u2 f1) ( f1, u2 ) ( f1, f1) 0

( f1,u2 ) (u1,u2 ) 1 ( f1, f1) (u1,u1) 5

f2 u2 12 f1 15 ( 1;2;0) (1;0;2) ( 54 ; 52 ;2)

Теперь векторы f1, f2 ортогональны.

																				2		30
Нормируем их.								f			5 ,			f	2


								1													5
			1		2																5
h (			1	;	2		;0)			h	(		2				;				1			;	5		)
h (				;			;0)		,	h	(						;							;			)
	1	5				5			,	2			30								30				30
		5				5							30								30				30
2. 2		4 . Решим матричное уравнение (Ae 4 E)X 0 .
									2			2				2 x										0
																						1
( Ae 4E) X 2											5 1										x2					0
									2		1 5															0
									2		1 5							x3								0
2		2			2			2			2		2						1				1 1

	2	5 1							0		3 3										0 1				1
	2	1 5							0		3 3										0 0				0
	2	1 5							0		3 3										0 0				0

			2
Решением является	векторы U 2	С3	1	,	C3 0 , базисом	пространства
Решением является	векторы U 2	С3	1	,	C3 0 , базисом	пространства
			1
			1
решений является вектор u	( 2; 1;1)T .
3
Вектор u3 ( 2; 1;1) ортогонален векторам					u1 ( 1;1;0) и	u2 ( 1;0;1) ,

поскольку они относятся к различным собственным значениям и, как следствие,

																									(			2			1						1
векторам h1	и h2			. Нормируем его.													u3				6 , h3							2		;	1			;			1		)


																										6					6						6
				h (				1		;	2		;0)					h	(				2		;		1		;		5				)				h	(	2	;	1	;	1	)
Векторы				h (						;			;0)			,		h	(						;				;						)	,			h	(		;		;		)
Векторы				1		5					5					,	2						30			30					30					,		3		6		6			6
						5					5												30			30					30									6		6			6
составляют искомый ортономированный базис.
																1			2					2


																	5		30						6
																	5		30						6
Ортогональная матрица U																	2		1					1


																	5		30						6
																	5		30						6
																			5						1
																	0		5						1

																			30						6
																			30						6
																				1						2					2



																							5			30							6				y
																						2				1					1							1
Искомое преобразование X UY																																					y2

																							5			30					6
																							5			30					6
																						0				5						1					y3

																										30
																										30							6
x		1	y		2		y					2			y
x			y				y		2						y
1	5			1	30				2		6			3
	5				30						6

	2		y1		1			y2			1
x2															y3

	5				30						6
	5				30						6
					5		y2				1
x3					5						1				y3

					30						6
					30						6

Канонический вид квадратичной формы: f 2y12 2y22 4y32 .

Применим рассмотренный алгоритм приведения квадратичной формы к каноническому виду с помощью ортогонального преобразования для классификации кривых и поверхностей второго порядка.

Пример 4. Найти тип и каноническое уравнение кривой второго порядка

9x2 6y2 4xy 16x 8y 2 0

Решение. Рассмотрим уравнение кривой: 9x2 6 y2 4xy 16x 8y 2 0

			квадратичная часть
Выпишем матрицу квадратичной части:
Матрица квадратичной формы:	9	2
Матрица квадратичной формы:	A
		6
	2	6

Найдем корни характеристического уравнения							Ae E	0 .		5
Найдем корни характеристического уравнения							Ae E	0 .
			9	2
			9	2
	Ae	E	2	6	2	15 50 ( 5)( 10) 0			1		-
			2	6						10
									2

собственные значения.

Найдем собственные векторы, относящиеся к каждому собственному значению:

1 5 . Решим матричное уравнение									(Ae 5Е)X 0 .
4	2	x		0	4	2			2		1
					,
						1					0
2 1		y		0	2	1			0		0
Решением			являются		векторы		U		С	1		C 0	, базисом пространства
Решением			являются		векторы		U	1	С		,	C 0	, базисом пространства
								1	1	2		1
										2

решений является вектор u (1;2)T .						Нормируем его: h1 (								1		;		2			)


			1										5		5
													5		5
2 10 . Решим матричное уравнение (Ae 10Е)X 0 .
1	2	x	0		1	2		1		2
					,
	4					4
2	4	y	0		2	4		0		0
Решением		являются		векторы		U		С	2		, C		0 ,			базисом
Решением		являются		векторы		U	2	С			, C	2	0 ,			базисом
							2	2				2
										1
решений является вектор u ( 2;1)T						. Нормируем его: h2 (											2		;	1		)


			2												5					5
															5					5

H {h1, h2} - собственный ортонормированный базис.
Перейдем		к новым координатам						(x', y')		с	помощью					матрицы

пространства

перехода от

исходного ортонормированного базиса {i, j} к собственному ортонормированному

базису {h1, h2}

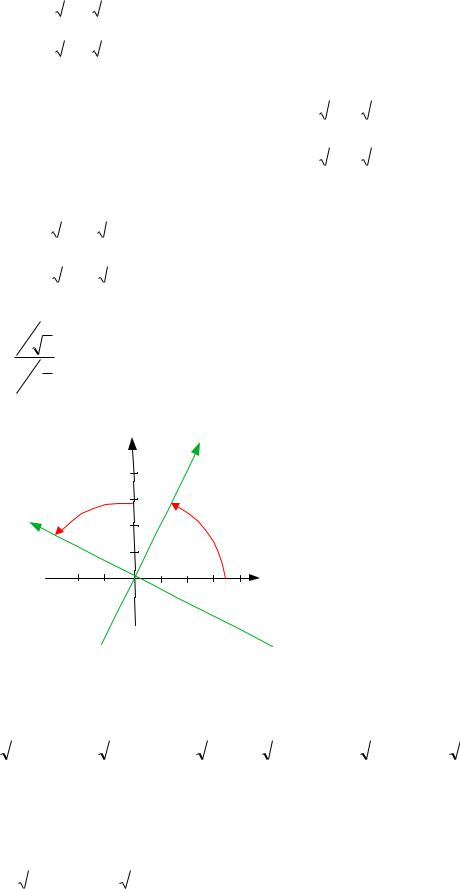
	1		2


	5	5
U	5	5		- матрица перехода
	2	1


	5	5
	5	5

		1
x	x'

		5

	U
Искомое преобразование		2
y	y'	2
y	y'
		5
		5

Выпишем преобразование координат:

2
	x'
5


1		.
1	y'
	y'
5
5

	1		2
x		x'		y' x'cos y'sin
x		x'		y' x'cos y'sin
	5		5
	2		1
y	2	x'	1	y' x'sin y'cos
y		x'		y' x'sin y'cos
	5		5
	5		5

Данное преобразование соответствуют повороту системы координат на угол :

tg 1 5 2 против часовой стрелки (т.к. угол положительный): по y 2 единицы,

по x - 1 единица

	y	x'
	4
y'	3
y'	2
	2

	1
		x
-3 -2 -1 0 1 2 3 4

Перейдем к новым координатам, подставив x' и y' в уравнение кривой:

x' 2 y' 2			2x' y' 2		x' 2 y'		2x' y'		x' 2 y'			2x' y'
9		6			4				16		8			2	0


	5			5		5		5		5			5

Раскроем скобки и приведем подобные слагаемые:

9	x'2	4x' y' 4 y'2			6		4x'2	4x' y' y'2 2			4	2x'2 3x' y' 2 y'2
5	x'2	4x' y' 4 y'2			5		4x'2	4x' y' y'2 2			5	2x'2 3x' y' 2 y'2
5					5						5
	16x' 32 y'			16x' 8y'
									2	0


			5			5

1 / 21 2 > Следующая >>>

Соседние файлы в папке Лекции Пронина Е.В.

#
02.06.2020641 Кб32Лекция 10.pdf
#
02.06.2020742 Кб43Лекция 11.pdf
#
02.06.2020722 Кб42Лекция 12.pdf
#
02.06.2020876 Кб35Лекция 13.pdf
#
02.06.2020774 Кб34Лекция 14.pdf
#
02.06.2020849 Кб39Лекция 15.pdf
#
02.06.2020955 Кб31Лекция 16.pdf