
2-й семестр / Лекции Пронина Е.В. / Лекция 13
.pdf
1
ОБОБЩЕНИЕ И СИСТЕМАТИЗАЦИЯ ЗНАНИЙ ПО ТЕМЕ
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
Пример 1. Найти длины элементов p(t) 3t 2 , |
|
q(t) t 3 евклидова про- |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
произведением ( p, q) |
|
p(t)q(t)dt . |
||||||||||||||||||
странства всех многочленов P [t] со |
скалярным |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
Найти угол между этими элементами. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Решение. Чтобы найти длины элементов p и q, найдем скалярные квадраты |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
(3t 2)3 |
|
1 |
|
|
125 |
|
|
1 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
( p, q) (3t 2)(3t 2)dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|||||||||||||||||||
|
9 |
|
|
|
|
9 |
|
|
9 |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
p |
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
(t 3)3 |
|
1 |
64 |
|
|
|
8 |
|
|
|
|
56 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
(q, q) (t |
3)(t 3)dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
3 |
|
3 |
|
3 |
|
3 |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
q |
|
|
56 |
|
|
2 |
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Нам понадобится скалярное произведение векторов p и q.
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
( p, q) (3t |
2)(t 3)dt (3t 2 11t 6)dt |
|
||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
|
11t |
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
t3 |
|
|
6t |
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
cos ( p, q) |
|
( p, q) |
|
14 |
|
|
|
|
|
|
3 |
|
|
|
||||||||||||||||
|
|
p |
|
|
|
q |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
56 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Значит ( p, q) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример 2. Найти длины элементов |
f (x) sin x , |
g(x) cosx евклидова про- |
||||||||||||||||||||||||||||
странства С[ , ] |
всех функций, непрерывных отрезке [ , ] со скалярным произведе- |
|||||||||||||||||||||||||||||
нием ( f , g) f (x)g(x)dx
Решение. Чтобы найти длины элементов f и g, найдем скалярные квадраты

2
(sin x, sin x)
f 
(cos x, cos x)
g 
|
|
1 |
|
1 |
|
sin 2x |
|
|
|
|
|
||||||||
|
sin 2 xdx |
|
(1 cos 2x)dx |
|
x |
|
|
|
|
|
|
|
|||||||
|
|
2 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|||||
|
1 |
|
1 |
|
sin 2x |
|
|
|
|
||||||||
cos2 xdx |
|
(1 cos 2x)dx |
|
x |
|
|
|
|
|
|
|
||||||
|
2 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|||||
Для нахождения угла нам понадобится скалярное произведение векторов f и g.
|
|
1 |
|
cos 2x |
|
( f , g) (sin x, cos x) |
sin x cos xdx |
|
sin 2xdx |
|
|
2 |
4 |
||||
|
|
|
0
cos ( f , g) |
|
( f , g) |
|
0 |
|
|
|
0 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
f |
g |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Значит ( f , g) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 3. Найти длины элементов |
p(t) 1 2t t 2 , q(t) 2 t евклидова |
|||||||||||||||||
пространства |
всех |
многочленов |
|
P2[t] |
со |
скалярным |
произведением |
|||||||||||
( p, q) p(0)q(0) p(1)q(1) p(2)q(2) . Найти угол между этими элементами.
Решение. В этой задаче удобно сначала записать значения заданных многочле-
нов при t=0, 1, 2.
p(0) 1, p(1) 0, p(2) 1 q(0) 2, q(1) 1, q(2) 0
Чтобы найти длины элементов p и q, найдем скалярные квадраты
( p, p) p(0) p(0) p(1) p(1) p(2) p(2) 1 1 0 0 1 1 2 p 
 2
2
(q, q) q(0) q(0) q(1) q(1) q(2) q(2) 2 2 1 1 0 0 5 q 
 5
5
Для нахождения угла, найдем скалярное произведение ( p, q)
( p, q) p(0) q(0) p(1) q(1) p(2) q(2) 1 2 0 1 1 0 2
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
cos ( p, q) |
( p, q) |
|
|
|
2 |
|
|
|
|
2 |
10 |
|
|
10 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
p |
q |
|
2 5 |
10 |
5 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Значит ( p, q) arccos |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

|
|
|
|
|
|
3 |
Пример 4. В базисе {e1,e2,e3} |
пространства E3 скалярное произведение задано |
|||||
8 |
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
матрицей Грама Г |
3 |
2 |
0 |
|
. Найти |
длины базисных векторов и угол между ними. |
|
1 |
0 |
1 |
|
|
|
|
|
|
|
|||
Найти длины векторов x и y пространства E3 , если x e1 2e2 e3, y 2e1 e3
Решение
1) Составим матрицу Грама в базисе {e1,e2,e3} :
|
(e , e ) |
(e , e ) |
(e , e ) |
||||
|
1 |
1 |
1 |
2 |
1 |
3 |
|
Г |
(e2 , e1) (e2 , e2 ) |
(e2 |
, e3 ) . |
||||
|
(e3, e1) |
(e3, e2 ) |
|
|
|
||
|
(e3, e3 ) |
||||||
|
(e , e ) (e , e ) |
(e , e ) |
8 |
3 |
1 |
||||||
|
1 |
1 |
1 |
2 |
1 |
3 |
|
|
|
|
|
Тогда |
(e2 |
, e1) |
(e2 |
, e2 ) |
(e2 |
, e3 ) |
= |
3 |
2 |
0 |
|
|
(e3, e1) (e3, e2 ) |
|
|
|
1 |
0 |
1 |
|
|||
|
(e3, e3 ) |
|
|
||||||||
(e1, e1) 8 e1 
 (e1, e1) 2
(e1, e1) 2
 2 , (e2 , e2 ) 2 e2
2 , (e2 , e2 ) 2 e2 
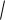 (e2, e2 )
(e2, e2 ) 
 2 ,
2 ,
|
|
|
|
|
|
|
|
(e , e ) |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
cos (e , e |
) |
1 |
2 |
|
|
|
|
|
|
|
(e , e ) arccos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
1 |
2 |
|
|
|
|
e |
|
|
|
|
e |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(e3, e3) 1 |
e3 |
(e3, e3) 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
(e , e ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||||||||||||||||||||||||
cos (e , e ) |
|
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(e , e ) arccos |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
1 |
3 |
|
|
|
|
e |
|
|
|
|
|
e |
|
|
|
|
|
|
2 |
|
2 |
|
|
|
4 |
|
|
|
|
|
1 |
3 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, e ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
cos (e , e ) |
(e2 , e3 ) |
|
0 |
0 (e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
2 |
3 |
|
|
|
e2 |
|
e3 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos (x, y) |
|
(x, y) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
2) |
x |
(x, x) , |
|
|
|
y |
|
|
|
( y, y) , |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
3 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(x, x) X T ГX = (1 2 |
|
|
1) |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
3 |
2 0 |
|
= 7 |
x |
(x, x) 7 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
3 |
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
( y, y) Y T ГY = (2 0 |
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
3 |
2 0 |
|
0 |
= 29 |
y |
( y, y) 29 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Для нахождения угла между векторами, найдем сначала скалярное произведе-
ние (x, y)

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
8 |
3 |
1 |
|
|
|
2 |
|
||||
(x, y) X T ГY = (1 |
2 |
1) |
3 |
2 |
0 |
|
|
|
0 |
= 4 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
|
|
|
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos (x, y) |
|
|
|
4 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
7 29 |
203 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(x, y) arccos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
203 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Задание *. В пространстве |
P [t] многочленов степени не выше 3-х скалярное |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
1
произведение задано формулой ( p, q) t2 p(t)q(t)dt . Показать евклидовость ска-
0
лярного произведения ( p, q) . Проверить, что для векторов p(t) 1 t 2 , q(t) t вы-
полнено неравенство Коши-Буняковского. Составить матрицу Грама скалярного про-
изведения в каноническом базисе пространства {1,t,t 2} . Записать скалярное произве-
дение в векторно-матричной форме.
ОРТОГОНАЛИЗАЦИЯ БАЗИСА
Ортонормированный базис Линейная независимость ортогональной системы векторов
Определение 1. Два вектора x и y называются ортогональными, если их ска-
лярное произведение равно 0, т.е.
Обозначается x y.
Свойства ортогональных векторов:
1. Два ненулевых вектора x и y ортогональны тогда и только тогда, когда угол между ними равен .
(x, y) 0 (x, y) 2 .
2.Нулевой вектор и только он ортогонален каждому вектору пространства.
3.Если вектор ортогонален самому себе, то он нулевой.
4.Если x y, то x y , , R

5
Определение 2. Система векторов x1, x2,..., xn называется ортогональной, ес-
ли все векторы системы попарно ортогональны, т.е. (xi , x j ) 0 при i j
Свойства ортогональной системы векторов
1. Теорема 1. Ортогональная система ненулевых векторов линейно независима.
Доказательство. Пусть векторы x1, x2,..., xn попарно ортогональны. Рассмот-
рим равенство нулевому вектору пространства линейной комбинации этих векторов:
1x1 2x2 ... n xn 0
Умножим обе части этого равенства скалярно на вектор x1 :
( 1x1 2x2 ... n xn , x1) (0, x1) .
Пользуясь аксиомой II скалярного произведения (линейность по первому со-
множителю):
( 1x1, x1) ( 2x2, x1) ... ( n xn , x1) (0, x1) .
Пользуясь аксиомой III скалярного произведения:
1(x1, x1) 2 |
(x2 |
, x1) ... n (xn , x1) |
(0, x1) . |
|
|
||||||
|
|
|
|
|
|
||||||
|
|
|
0 |
|
|
|
0 |
0 |
|
|
|
Следовательно |
|
1 |
|
|
x |
|
2 0 , так как x |
0 , |
то остается |
0 . |
|
|
|
||||||||||
|
|
|
|
1 |
|
1 |
|
1 |
|
|
|
Применяя этот прием, получаем, что 2 |
... k 0 |
|
|
||||||||
Получаем, |
|
что |
рассматриваемая |
линейная |
комбинация |
||||||
1x1 2x2 ... n xn 0 |
тривиальная. Значит, |
ортогональная |
система векторов |
||||||||
x1, x2,..., xn линейно независима. Что и требовалось доказать.
2. Равенство нулю суммы взаимно ортогональных векторов возможно только в случае, если каждое из слагаемых есть нулевой вектор пространства.
3. Если вектор x ортогонален каждому вектору системы x1, x2,..., xn , то он ор-
тогонален и любой их линейной комбинации.
4. Обобщение теоремы Пифагора.
Для ортогональной системы векторов x1, x2,..., xn верно утверждение:
x1 x2 ... xn 2 x1 2 x2 2 ... xn 2
Задание *. Доказательство провести самостоятельно.

|
|
|
|
|
|
|
|
|
|
|
|
6 |
||
|
|
Определение 3. Вектор x |
|
называется нормированным или единичным, если |
||||||||||
x |
|
1 |
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Если x ≠ 0 вектор, то x |
|
|
|
|
( x |
|
|
|
|
) есть нормированный вектор. Нахож- |
||
|
|
|
|
x |
|
|
|
|
x |
|
|
|||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дение для данного вектора нормированного ему вектора называется нормированием вектора.
Множитель |
|
1 |
|
|
есть нормирующий множитель. |
|
|
|
x |
|
|
||
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение 4. Система векторов x1, x2,..., xn называется ортонормирован-
ной, если все векторы этой системы попарно ортогональны и длина (норма) каждого
вектора системы равна единице, т.е.
1, |
i j |
(xi , x j ) |
i j |
0, |
Определение 5. Базис e1, e2 ,..., en евклидова пространства называется орто-
нормированным, если все его векторы попарно ортогональны и длина каждого из них
равна единице, т.е.
1, |
i j |
|
|
(ei , e j ) |
i j |
|
|
0, |
|
|
|
Теорема 2. (Метод Грама-Шмидта). В конечномерном n-мерном евклидовом |
|||
пространстве существует ортонормированный базис. |
|
||
Доказательство. Пусть e1, e2,..., en - некоторый базис данного евклидова про- |
|||
странства En . |
|
|
|
Сначала сформируем новый ортогональный базис |
f1, f2,..., fn . |
||
Составим ортогональную систему векторов следующим образом: |
|||
1. Пусть f1 e1 |
|
|
|
2. f2 зададим, как f2 e2 21 f1 , где |
21 - |
некоторый коэффициент. По- |
|
скольку e1 и e2 линейно независимы, то вектор |
f2 0 при любом значении 21 . |
||
Подберем 21 |
таким образом, чтобы векторы f1 |
и f2 были ортогональны (ор- |
|
тогональность означает равенство нулю их скалярного произведения):

7
( f1, f2 ) ( f1, e2 |
21 f1) 0 ( f , e ) ( f , f ) 0 |
||
|
|
1 2 |
21 1 1 |
e1 |
e1 |
|
|
|
|
|
( f1, e2 ) |
( f1, e2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
21 |
|
|
( f1, f1) |
|
|
|
f |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Графически, в пространстве геометрических векторов, это можно представить |
|||||||||||||||||||||||||||||||||
следующим образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Первоначальный базис пространства |
|
|
|
Ортогональный базис, |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
полученный из исходного |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
e1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3. |
f3 зададим следующим образом: |
|
f3 e3 31 f1 32 f2 , |
где 31 , |
32 |
- не- |
|||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
которые коэффициенты, подобранные таким образом, чтобы векторы f3 и |
f1 , |
f3 и |
||||||||||||||||||||||||||||||||
f2 |
были ортогональны: ( f3, f1) 0 , ( f3, f2 ) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
( f1, f3) ( f1, e3 31 f1 32 f2 ) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
( f , e ) ( f , f ) |
( f , f |
|
|
) 0 |
( f1, e3 ) |
|
( f1, e3 ) |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
1 |
3 |
|
31 |
1 |
1 |
32 |
1 |
2 |
|
31 |
( f1, f1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
2 |
|
|
|
|
|
|
||||||||||||
e1 |
|
|
|
e1 |
e1 1 |
|
|
0 т.к. f1 f 2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
( f2, f3) ( f2, e3 31 f1 32 f2 ) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
( f2 |
, e3 ) 31 |
( f1, f2 ) |
32 ( f2 , f2 ) 0 32 |
|
( f2 , e3 ) |
|
( f2 , e3 ) |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( f2 , f2 ) |
|
|
|
|
|
|
f |
2 |
|
|
|
|
|
||||
|
|
|
|
0 т.к. f1 f 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Графически, в пространстве геометрических векторов, это можно представить
следующим образом:
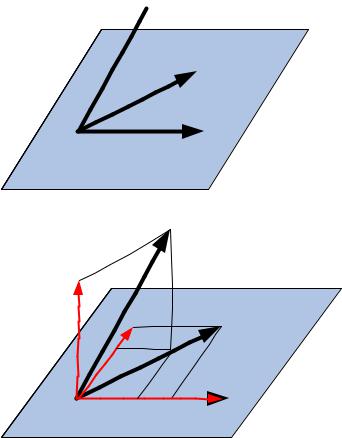
8
 e3
e3
e2
e1
|
|
|
|
|
|
|
|
|
Исходный базис |
|
|
|
||||||
|
|
|
|
|
e3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f3 |
|
e3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
f2 |
|
e2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
f1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e1 |
|
|
|
Ортогональный базис |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k. Пусть уже найдены взаимно ортогональные векторы f1, f2,..., fk 1 . Вектор |
|||||||||||||||||
fk |
выберем таким образом, чтобы он был ортогонален каждому из векторов уже по- |
|||||||||||||||||
строенной |
системы |
f1, f2,..., fk 1 . |
В качестве |
|
|
fk |
|
возьмем |
вектор |
|||||||||
fk |
ek k1 f1 k 2 f2 |
... k,k 1 fk 1. Рассуждая, как и ранее, |
получаем, |
что век- |
||||||||||||||
тор |
fk 0 при любых |
значениях |
|
k1, k 2 ,..., k,k 1 . |
Из условий ортогональности |
|||||||||||||
( fk , f j ) 0 |
|
|
|
|
|
|
kj |
( f j , ek ) |
|
( f j , ek ) |
|
|||||||
находим последовательно |
|
|
|
|
|
|
|
, j 1,2,..., k 1. |
||||||||||
( f j , f j ) |
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
f j |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Продолжая этот |
процесс, |
мы |
построим новую |
ортогональную |
систему |
||||||||||||
f1, f2 ,..., fn . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Делением каждого элемента |
|
fk |
на его длину, получаем ортонормированную |
||||||||||||||
систему векторов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
9
h1 |
|
f1 |
, h2 |
|
f2 |
, …, hn |
|
fn |
. |
|
f1 |
|
f2 |
|
fn |
||||
|
|
|
|
|
|
|
Процесс построения по данному базису ортонормированного базиса называется ортогонализацией данного базиса.
Описанный при доказательстве метод носит название метода Грама-Шмидта.
Теорема 3. Скалярное произведение векторов в ортонормированном базисе имеет единичную матрицу Грама.
Доказательство.
Пусть h1, h2,..., hn - ортонормированный базис. То есть
1, |
i j |
|
|
(h1, h1) |
(h1, h2 ) ... |
(h1, hn ) |
|
1 |
0 |
... |
0 |
|||||
(hi , h j ) |
|
, тогда Г |
|
(h , h ) |
(h , h ) ... |
(h , h ) |
|
|
|
0 |
1 |
... |
0 |
|
||
0, |
i j |
|
|
|
2 1 |
2 2 |
2 |
n |
|
|
|
|
|
|
|
|
|
|
|
(hn , h1) |
(hn , h2 ) ... |
(h2 |
, hn ) |
|
|
|
0 |
0 |
... |
1 |
|
||
|
|
|
|
|
|
|
|
|
||||||||
Следствие |
1. Если в |
ортонормированном |
базисе |
|
заданы |
векторы |
||||||||||
x (x1, x2 ,..., xn ) , |
y ( y1, y2,..., yn ) , |
то их скалярное произведение находится по |
||||||||||||||
формуле (x, y) x1y1 x2 y2 ... xn yn .
Доказательство.
Так как в ортонормированном базисе
1 |
0 ... |
0 |
|
|
|
|
|
|
|
|
|
Г |
0 |
1 ... |
0 |
|
, то |
|
0 |
0 ... |
1 |
|
|
|
|
|
|||
|
x1 |
|
|
1 |
0 ... |
0 |
|
|
|
|
|
|
|
|
|
|
|
(x, y) X T ГY |
... |
|
|
|
0 |
1 ... |
0 |
|
y ... |
y |
n |
x y |
x y |
2 |
... x y |
n |
|
|
|
|
|
|
|
|
|
1 |
|
1 1 |
2 |
n |
|||||
|
|
|
|
|
0 |
0 ... |
1 |
|
|
|
|
|
|
|
|
|
|
|
xn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 5. В пространстве R3 |
задан |
базис |
|
e1 (1, 1,1) , |
e2 (2, 3,4) , |
||||||||||||
e3 (2,2,6) . Скалярное произведение задается формулой (x, y) x1y1 x2 y2 x3 y3 .
Ортогонализировать данный базис.
Решение.
Сформируем новый ортогональный базис f1, f2, f3 .
1.Пусть f1 e1 (1, 1,1)
2.f2 зададим, как f2 e2 21 f1 , где 21 - некоторый коэффициент.

10
|
|
Подберем 21 таким образом, чтобы векторы |
|
f1 и |
f2 |
были ортогональны: |
|||||||||||||||||||||||||||||||||||||
|
|
( f1, f2 ) ( f1, e2 |
21 f1) 0 |
( f , e ) ( f , f ) 0 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
21 |
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
e1 |
|
|
|
e1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
21 |
( f1,e2 ) ( f1,e2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
( f1, f1) |
|
|
f |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( f1, e2 ) = (e1, e2 ) 1 2 ( 1) ( 3) 1 4 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
( f1, f1) = (e1,e1) 1 1 ( 1) ( 1) 1 1 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
9 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
21 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
f2 e2 |
|
3 f1 e2 3e1 (2; 3;4) 3(1; 1;1) ( 1;0;1) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
3. |
|
f3 e3 31 f1 32 f2 , где 31 , 32 |
- некоторые коэффициенты, подобран- |
||||||||||||||||||||||||||||||||||||||
ные таким образом, чтобы векторы f3 и |
f1 , f3 |
и f2 |
|
были ортогональны: ( f3, f1) 0 |
|||||||||||||||||||||||||||||||||||||||
, ( f3, f2 ) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
( f1, f3) ( f1, e3 31 f1 32 f2 ) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
( f , e ) ( f , f ) |
|
( f , f |
|
) 0 |
( f1, e3 ) |
|
( f1, e3 ) |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
1 |
3 |
|
|
|
|
31 |
1 |
1 |
|
|
32 |
1 |
2 |
|
31 |
|
|
( f1, f1) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
2 |
|
|
|
|
||||||||||||||||||
e1 |
|
|
|
|
|
|
e1 |
e1 |
|
|
0 т.к. f1 f 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
( f1, e3 ) = (e1,e3 ) 1 2 ( 1) 2 1 6 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
( f1, f1) = (e1,e1) 1 1 ( 1) ( 1) 1 1 3 |
|
|
f1 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
6 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
31 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
( f2, f3) ( f2, e3 31 f1 32 f2 ) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
( f2 , e3 ) 31 |
( f1, f2 ) |
32 ( f2 , f2 ) |
0 32 |
|
( f2 , e3 ) |
|
( f2 , e3 ) |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( f2 , f2 ) |
|
|
|
|
|
|
f |
2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
0 т.к. f1 f 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
( f2 , e3) = ( f2 ,e3 ) ( 1) 2 0 2 1 6 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
( f2 , f2 ) ( 1) ( 1) 0 0 1 1 2 |
|
|
|
|
f2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
32 42 2
f3 e3 2 f1 2 f2 (2;2;6) 2(1; 1;1) 2( 1;0;1) (2;4;2)
|
|
|
|
|
( f3, f3 ) 2 2 4 4 2 2 24 |
|
f3 |
2 6 |
|
