2.7.2 Расчет передачи на выносливость зубьев при изгибе.

Для косозубых колес проверка проводится по формуле:

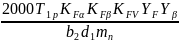
_F = _FP

Коэффициент торцового перекрытия

ε_α= cos(β) = cos(1,55) = 1,46

Коэффициент, учитывающий распределение нагрузки между зубьями

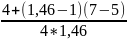= = = 0,84

Коэффициент, учитывающий влияние динамической нагрузки

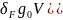= 1+ = 1+ 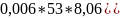= 3,95

_F =

Общее передаточное отношение привода:

.

Намечаем частные передаточные отношения редуктора.

По формулам из таблицы 1.3 [3] имеем:

;

.

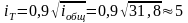Получаем .

Отклонение , что меньше допускаемого .

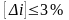Частоты вращения и угловые скорости валов редуктора:

ведущего вала редуктора

;

;

промежуточного вала редуктора

;

;

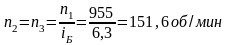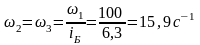ведомого вала редуктора

;

.

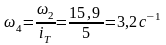2.4. Определение вращающихся моментов на валах

Вращающийся момент на валу электродвигателя (на входном валу редуктора): .

Вращающийся момент на промежуточном валу редуктора:

Вращающийся момент на выходном валу редуктора:

.

3. Расчет зубчатых колес редуктора

Рис.2. Кинематическая схема цилиндрического двухступенчатого соосного редуктора

Так как в задании нет особых требований в отношении габаритов передачи, выбираем материалы со средними механическими характеристиками. По таблице 3.3 [2] принимаем для шестерен сталь 45 улучшенную с твердостью НВ 230; для колес сталь 45 улучшенную с твердостью НВ 200.

Редуктор нереверсивный, предназначен для длительной эксплуатации; работа односменная; валы установлены на подшипниках качения.

3.1. Определение допускаемых контактных напряжений

Допускаемые контактные напряжения на поверхности зубьев цилиндрических колес при проектном расчете

,

здесь 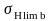– предел контактной выносливости при базовом числе циклов (принимаем по таблице 3.2 [2]):

= .

Коэффициент долговечности при длительной эксплуатации редуктора K_HL = 1. Коэффициент запаса прочности выбирается в пределах 1,1÷1,2, принимаем = 1,15.

Принимаем значения коэффициента нагрузки для случая несимметричного расположения колес К_Нβ = 1,25 (таблица 3.1 [2]).

Коэффициенты ширины венцов по межосевому расстоянию для быстроходной ступени и для тихоходной ступени (так сделано потому, что тихоходная ступень более нагружена, чем быстроходная).

3.2. Расчет тихоходной передачи

3.2.1. Определение межосевого расстояния из условия контактной выносливости поверхностей зубьев

В соосном редукторе межосевые расстояния быстроходной и тихоходной ступеней равны: а_Б = а_Т.

Межосевое расстояние из условия контактной выносливости активных поверхностей зубьев определяется по формуле:

= =246 мм.

Здесь принято .

Округляем межосевое расстояние до ближайшего значения по стандарту СТ СЭВ 229-75 (мм): по первому ряду выбираем а_ω = 250 мм.

3.2.2. Определение нормального модуля

Нормальный модуль:

.

По стандарту СТ СЭВ 310-76 (мм) по первому ряду выбираем m_nТ = 4.

3.2.3. Определение основных размеров шестерни и колеса

Принимаем предварительно угол наклона зубьев β = 10˚и определяем число зубьев шестерни:

= . Принимаем z₃ = 20.

Тогда число зубьев колеса: .

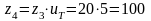Проверим межосевое расстояние.

Для косозубых колес со стандартным модулем:

.

При проверке обнаружилось несоответствие полученного результата с ранее принятым значением, а_ωТ = 250 мм по стандарту. В этом случае надо устранить расхождение изменением угла β по формуле:

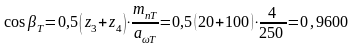; β = 16˚15^’.

Теперь проверяем расчеты, определив диаметры делительных окружностей:

;

.

Проверка: = .

Диаметры вершин зубьев:

;

.

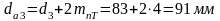Ширина колеса и шестерни:

;

.

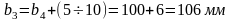Определяем коэффициент ширины шестерни по диаметру:

.