11.2. Включение цепи е резистором и конденсатором на постоянное напряжение (заряд конденсатора)

Из схемы, приведенной на рис. 11.1, следует, что установившаяся составляющая напряжения на конденсаторе 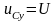, а свободная составляющая, очевидно, равна

Рис. 11.3.

Полагаем, что до замыкания ключа конденсатор не был заряжен (U_C(0.) = 0). На основании законов коммутации u_C(0-) = u_C(0+) = 0, при t = 0; следовательно:

u_c(0) = u_cy(0) + u_cсв(0) или 0 = U + А, откуда А = -U.

Тогда переходное напряжение на конденсаторе

а переходный ток в цепи

Зависимости напряжений и токов от времени показаны на рис. 11.3. Из них видно, что напряжение на конденсаторе возрастает по экспоненциальному закону от нуля до напряжения источника, а ток уменьшается от начального значения до нуля также по экспоненте. Длительность их изменения определяется постоянной времени τ = RC. Здесь как и в п. 11.1 время переходного процесса принимается равным t ≈ (3÷5)τ.

11.3. Включение цепи с резистором и конденсатором на синусоидальное напряжение

Пусть напряжение источника изменяется по закону

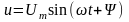
Рис. 11.4

Установившаяся составляющая напряжения на конденсаторе (см. рис. 11.4) равна:

где: 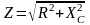- полное сопротивление цепи;

Хс = 1 / (ωC) - емкостное сопротивление;

φ = -arctg(Xc/R) - угол сдвига фаз между установившимся током в цепи и приложенным синусоидальным напряжением.

Свободная составляющая напряжения на конденсаторе

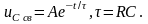
Переходное напряжение на конденсаторе

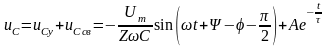
Рис. 11.5

Полагая, что u_C(0-) = 0, для постоянной интегрирования получим

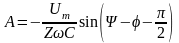
Окончательно напряжение на конденсаторе можно записать в виде

Ток в цепи

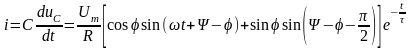
Зависимости переходного напряжения на конденсаторе от времени при различных значениях разностей ψ-φ показаны на рис. 11.5. Их анализ позволяет сделать следующие выводы.

Если в момент включения мгновенное значение установившегося напряжение на конденсаторе равно нулю (ψ - φ - π / 2 = 0), то и свободная составляющая напряжения равна нулю. В цепи сразу устанавливается режим (рис. 11.5 а).

Если в момент включения мгновенное значение установившегося напряжение на конденсаторе имеет наибольшее значение (ψ - φ - π / 2 = π / 2), то переходное напряжение достигает максимального значения приблизительно через половину периода и может приблизиться к удвоенной амплитуде установившегося напряжения, но не превысит его (рис. 11.5 в).

Вопросы для самопроверки.

1. Написать расчёт переходного процесса при разряде заряженного конденсатора на сопротивление.

2. Нарисовать графики изменения переходного напряжения (постоянной и свободной составляющих) на конденсаторе в RC цепи при заряде конденсатора от источника постоянного напряжения.

3. Определите примерное время окончания переходного процесса разряда конденсатора ёмкостью в 15 мкФ на сопротивление 4 кОм.

4. Установившаяся составляющая напряжения на конденсаторе при подключении его через резистор на синусоидальное напряжение . Формула.

5. Уравнение свободной составляющей напряжения на конденсаторе при подключении его через резистор на синусоидальное напряжение.

6. В каком случае отсутствует свободная составляющая напряжения на конденсаторе при подключении его через резистор на синусоидальное напряжение?

7. В каком случае напряжение на конденсаторе при переходном процессе может приблизится к удвоенной амплитуде установившегося напряжения?

Лекция 12.