Билет №1

1)Основные положения. Теория теплообмена

Теория ТМО рассм. пр-сы переноса теплоты и массы в тв., жидких и газооб. телах. Пр-сы переноса теплоты – это обмен внутр. э. м/д телами в форме теплоты. Э.-общ. кол-ная мера различных форм движения материи. Тепловая э.- универ. форма э., возник. в рез. теплового движ. молекул.

Теплота (как и работа) – форма передачи энергии.

Теплообмен – самопроизвольный необратимый пр-с переноса теплоты в прост-ве с неоднор. темп-ым полем. Различают три элементарных вида теплообмена: теплопроводность; конвекция и лучеиспускание (тепловое излучение).

Т/про-ть – молек-ый перенос теплоты в сплошной среде из-за наличия градиента температуры. В чистом виде только ТВ. телах. В диэлектриках и жидкостях т/пр-ть осущ. за счёт упругих волн молекул; в Ме и сплавах – за счёт перемещения свободных электронов и колебания атомов; в газах – за счёт диффузии атомов и молекул. (q,λ)

Конвекция – перенос теплоты самой средой из области высок. t в обл. низ. t,к-рая в движ. средекапел. ж-ти или газа,сопровож. т/пр-тью.(α)

Тепл. излучение (лучистый теплообмен) – т/обмен, обусл. превращением внутр. э. одного тела в э. э/магн. волн, распр. её в прост-ве и поглощ. э. этих волн др. телом,превращ. в тепл. э. Перенос теплоты путём теплопроводности и конвекции возможны только при наличии вещественной среды. Лучистый теплообмен может осуществляться и в вакууме.

Теплопередача – перенос теплоты от одного теплоносителя к другому через разделяющую их стенку или перегородку.

2) Турбулентный перенос теплоты и кол-ва движения в пограничном слое

Отклонения мгновенной скорости потока , от средней во времени называются пульсациями скорости или пульсационными скоростями. При этом скорость равна

, где  – пульсационная скорость

Таким образом, турбулентное движение состоит из регулярного течения и наложенного на него хаотического пульсационного течения (см. рис. 12.4).

Пульсации скорости приводят к переносу теплоты, вследствие чего возникают пульсации температур. Поэтому турбулентное течение не является стационарным.

Зависимость среднего коэффициента теплоотдачи и локального коэффициента теплоотдачи от коэффициента трения аналогична как для турбулентного режима течения (соблюдается гидродинамическая аналогия теплообмена Рейнольдса).

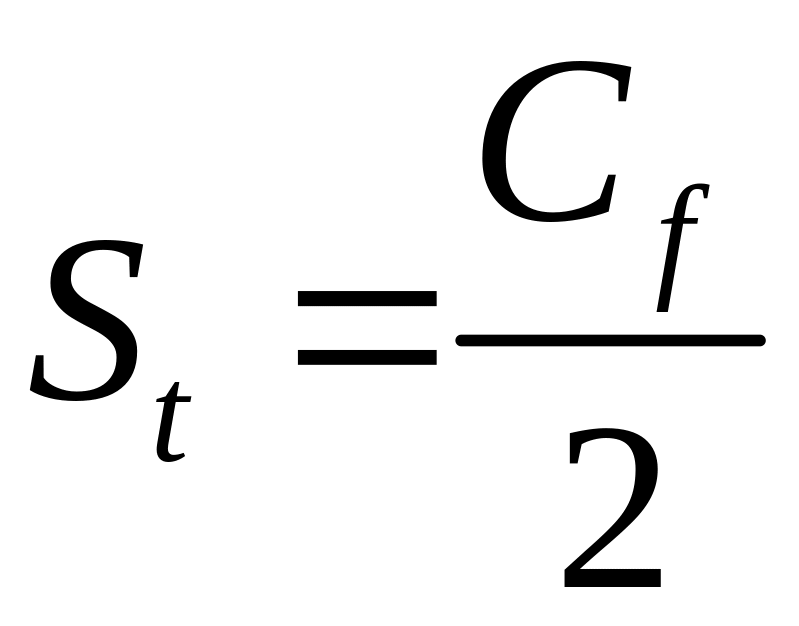(12.24)

Билет №2

1) Температурное поле

Аналитически распределение температуры в теле описывается с помощью уравнения:

. (1.1)

Это математическое описание температурного поля в теле.

Если температура в данной точке не меняется по времени, т.е. то такое температурное поле называется стационарным, если наоборот, если то такое температурное поле называется нестационарным.

Если температура меняется только вдоль одной из координат (пусть х), то такое температурное поле называется одномерным:

, .

Для двухмерного нестационарного температурного поля:

, .