2.5 Сложные учетные ставки

Наращенная сумма по прошествии n лет составит:

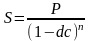
Для начисления процентов k раз в год формула примет вид:

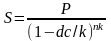
2.6 Аннуитеты

В большинстве современных коммерческих операций подразумеваются не разовые платежи, а последовательность денежных поступлений (или наоборот выплат) в течение определенного периода. Такая последовательность называется потоком платежей.

Поток однонаправленных платежей с равными интервалами между последовательными платежами в течение определенного количества лет называется аннуитетом (финансовой рентой)

Аннуитет – это денежный поток, в котором все суммы возникают не только через одинаковые промежутки времени, но и являются равновеликими.

Аннуитет (финансовая рента) – ряд последовательных фиксированных платежей, производимых через равные промежутки времени.

Примером аннуитета могут быть ежеквартальные суммы процентов по облигациям или сберегательным сертификатам, равномерная уплата взносов за арендуемое имущество выплаты в пенсионный фонд, погашение долгосрочного кредита и т.п. Аннуитет, для которого платежи осуществляются в начале соответствующих интервалов носит название аннуитета пренумерандо, если же платежи осуществляются в конце интервалов - постнумерандо (обыкновенный аннуитет) - самый распространенный случай.

Аннуитеты отличаются между собой следующими характеристиками:

- величиной каждого отдельного платежа

- интервалом времени между двумя последовательными платежами (периодом аннуитета)

- сроком от начала аннуитета до конца его последнего периода

- процентной ставкой, применяемой при наращении или дисконтировании платежей

Обобщающими показателями ренты являются наращенная сумма и современная (текущая и приведенная величина).

Наращенная сумма ренты – сумма всех членов потока платежей с начисленными на них на конец срока, т.е. на дату последней выплаты. Наращенная сумма показывает, какую величину будет представлять капитал, вносимые через равные промежутки времени в течение всего срока ренты с начисленными %.

При работе с рентами часто требуется оценить текущую стоимость аннуитета, текущая стоимость ренты может называться современная, настоящая, приведенная величина.

Последовательность денежных потоков (платежей) в виде аннуитета существенно упрощает процесс наращения или дисконтирования стоимости денег, дает возможность использовать набор упрощенных формул со стандартными значениями отдельных показателей, приводимыми в специальных таблицах.

Так, формула для определения будущей стоимости аннуитета имеет вид:

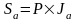
где: S_a - общая будущая стоимость аннуитета на конец определенного периода.

P - сумма аннуитетного платежа,

J_a - множитель наращения аннуитета, определяемый по специальным таблицам с учетом ставки процента и числа периодов.

Соответственно, формула для определения настоящей стоимости аннуитета имеет вид:

Р_а = P /R_а.

где: Р_а - настоящая стоимость аннуитета,

P - сумма аннуитетного платежа;

R_а - дисконтный множитель аннуитета, определяемый по специальным таблицам с учетом дисконтной ставки и числа периодов.

Рассмотрим аннуитет постнумерандо с ежегодными платежами P в течение n лет, на которые начисляются проценты по сложной годовой ставке i_c.

Найдем будущую величину (Sа) аннуитета.

Будущая стоимость аннуетета постнумерандо

0 1 2 3 n-1 n

P P P P P

S_n

S_n-1

S₃

S₂

S₁

S

Сумма S₁ для первого платежа, проценты на который будут начисляться, очевидно (n-1) раз составит:

S₁ = Р(1 + i_c)^n-1

Для второго платежа (проценты на него будут начисляться на один год меньше:

S₂ = Р(1 + i_c)^n-2

На последний платеж, произведенный в конце n-го года проценты уже не начисляются:

S_n = P

Тогда для общей наращенной суммы имеем:

(1 + i_c)ⁿ - 1

Sа = P --------------

i_c

Коэффициент наращения соответственно равен:

(1 + i_c)ⁿ - 1

k_n = --------------

i_c

Современная величина (Pа) аннуитета постнумерандо.

Современная величина аннуитета постнумерандо

0 1 2 3 n-1 n

P P P P P

Pа1

Pа2

Pа3

P а n-1

Pа n

A

При заданной процентной ставке i_c современное значение каждого платежа будет определяться по формуле:

P

Pа = --------------

(1 + ic)ⁿ

Современная величина всего аннуитета:

1- (1 + i_c)^-n

Pа = P _* ---------------------

i_c

Коэффициент дисконтирования соответственно равен:

1- (1 + i_c)^-n

kd = ---------------------

i_c

Текущая стоимость аннуитета часто используется в операциях с недвижимостью.

Некоторые ренты реализуются сразу после заключения контракта. Первый платеж производится немедленно, а последующие платежи - через равные интервалы. Такие ренты называют пренумеранда или авансовые или причитающимися аннуитетами.

Рассмотрим аннуитет пренумерандо с ежегодными платежами P в течение n лет, на которые начисляются проценты по сложной годовой ставке i_c.

Отличие от предыдущего случая здесь в том, что период начисления процентов на каждый платеж увеличивается на один год, т.е. каждая наращенная сумма S_k увеличивается в (1+i_c) раз.

(1 + i_c)ⁿ - 1

Sап = Sа (1 + i_c) = P -------------- (1 + i_c)

i_c

Для определения современных значений каждого платежа дисконтирование по заданной ставке i_c проводится на один раз меньше, чем в случае аннуитета пренумерандо. Поэтому каждая современная величина Pа будет больше в (1+i_c) раз.

1- (1 + i_c)^-n

Pап = Pа (1 + i_c) = P _* ---------------- (1 + i_c)

i_c

Аннуитетами может производиться погашение долга и такой аннуитет называется обязательным.

В экономической литературе часто употребляется выражение «расходы по обслуживанию долга», что означает погашение суммы самого долга (амортизация долга) и выплата % по нему. Участники сделки оговаривают способы погашения задолженности и план её погашения при заключении контракта. Наиболее часто применяется схема погашения кредита в конце каждого года равными срочными уплатами, включающими выплаты основной суммы долга и % по нему называется периодический взнос на погашение долга.

Формула периодического взноса по погашению долга (IAO)

IAO = P + i

Р - осн долг

i - % по долгу

IAO =D * ((i * (1 + i)ⁿ) / ((1 + i)ⁿ – 1)

D - величина долга

i * (1 + i)ⁿ - коэффициент погашения задолженности

Конверсия - такое изменение начальных параметров аннуитета, после которого новый аннуитет был бы эквивалентен данному.

Два аннуитета считаются эквивалентными, если равны их современные величины, приведенные к одному и тому же моменту времени.

На практике необходимость рассчитать параметры эквивалентного аннуитета чаще всего возникает при изменении условий выплаты долга, погашении кредита или займа. При этом конверсия может произойти как в момент начала аннуитета (на этот момент и рассчитываются современные величины эквивалентных аннуитетов), так и после выплаты некоторой части аннуитета. В этом случае все расчеты производятся на остаток долга в момент конверсии.

Распространенные случаи конверсии аннуитетов.

1. Через некоторый промежуток времени n₀ (он может = 0) после начала аннуитета весь остаток долга может быть выплачен за один раз (выкуп аннуитета). В этом случае величина выплачиваемой суммы будет равна современной величине остатка аннуитета, рассчитанной для срока n₁ = n - n₀

2. Задача, обратная предыдущей - задолженность погашается частями, в виде выплаты постоянного аннуитета и требуется определить один из параметров аннуитета при заданных остальных.

3. Период выплаты долга может быть изменен при сохранении прежней процентной ставки. Величину P₁ платежа для срока n₁ находим, используя уравнения эквивалентности (приравниваются современные значения аннуитетов):

1- (1 + i_c)^-n1 1 - (1 + i_c)^-n

P₁ -------------------- = P------------------

i_c i_c

отсюда:

1- (1 + i_c)^-n

P₁ = P ----------------

1- (1 + i_c)^-n1

Очевидно, что срок аннуитета увеличится, значение Р сократится и наоборот.

4. Может возникнуть ситуация, когда величина платежа Р должна быть изменена в ту или иную сторону.

5. Начало выплаты задолженности при заданной процентной ставке i_c может быть отсрочено:

а) при сохранении размера платежа

б) при сохранении срока выплаты.

В первом случае должен увеличиться срок аннуитета, во тором - величина платежа.

6. В некоторых случаях может потребоваться объединение нескольких аннуитетов в один (консолидация аннуитетов). При этом объединяемые аннуитеты могут быть любыми, а в искомом объединяющем аннуитете один из параметров неизвестен, при всех остальных заданных.

При планировании и анализе денежных потоков часто используют 6-ть функций сложного % (денежной единицы), отражающих временную оценку денег:

1) будущая стоимость денежной единицы (накопленная сумма единицы);

2) будущая стоимость аннуитета (накопление единицы за период, фонд накопления капитала);

3) текущая стоимость аннуитета;

4) текущая стоимость единицы (реверсии);

5) фактор фонда возмещения (периодический взнос в фонд накопления);

6) взнос на амортизацию денежной единицы (периодический взнос на погашение кредита).

Все шесть функций сложного % строятся с использованием общей базовой формулы (1 + i)ⁿ описывающей накопленную сумму единицы. Выделяют три основные функции, а остальные получают как обратные к ним величины.

Взаимосвязь между функциями сложного процента.

Функция	Обратная величина
(1 + i)n множитель наращения сложных %, т.е. накопленная величина денежной единицы	(1 + i)-n дисконтный множитель, т.е. текущая стоимость денежной единицы
(1 + i)n – 1 I коэффициент наращения ренты (коэффициент накопления денежной единицы за период)	i (1 + i)n – 1 фактор фонда возмещения денежной единицы
1 – (1 + i)-n I коэффициент приведения ренты, т.е. текущая стоимость аннуитета	i * (1 + i)n (1 + i)n – 1 взнос на амортизацию денежной единицы

Каждая из 6 функций предусматривает, что % приносят деньги, находящиеся а депозитном счете, причем только до тех пор, пока они остаются на этом счете. Каждая из них учитывает эффект сложного %, т.е. такого %, который, будучи полученным, переводится в основную сумму.