2.2 Простые ставки ссудных процентов

Простым процентом называется сумма, которая начисляется по первоначальной (настоящей) стоимости вклада в конце одного периода платежа, обусловленного условиями инвестирования средств (месяц, квартал и т.п.).

Простые ставки ссудных процентов применяются обычно в краткосрочных финансовых операциях, когда интервал начисления совпадает с периодом начисления (и составляет, как правило, срок менее одного года) или когда после каждого интервала начисления выплачиваются проценты.

При расчете суммы простого процента в процессе наращения вклада используется формула:

,

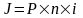где J - сумма процента за обусловленный период инвестирования в целом;

P - первоначальная сумма вклада (инвестиций);

n - продолжительность инвестирования (в количестве периодов, по которым осуществляется каждый процентный платеж);

i - процентная ставка (выраженная в десятичной дроби).

Будущая стоимость вклада (S) с учетом численной суммы процента определяется по формуле

.

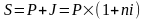Множитель (l+ni) называется множителем (коэффициентом) наращения простых процентов. Его значение всегда должно быть больше единицы.

При расчете процентов применяют две временные базы K = 360 дней (12 месяцев по 30 дней) или K = 365, 366 дней. Если K = 360 дней, то получают ОБЫКНОВЕННЫЕ или КОММЕРЧЕСКИЕ проценты, а при использовании действительной продолжительности года (365, 366 дней) рассчитывают ТОЧНЫЕ проценты.

Число дней ссуды также можно измерить приближенно и точно. В первом случае продолжительность ссуды определяется из условия, согласно которому любой месяц принимается равным 30 дням. В свою очередь точное число дней ссуды определяется путем подсчета числа дней между датой выдачи ссуды и датой ее погашения. День выдачи и день погашения считаются за один день.

На практике применяются три варианта расчета простых процентов.

1. Точные проценты с точным числом дней ссуды. Этот вариант дает самые точные результаты. Данный способ применяется центральными банками многих стран и крупными коммерческими банками. Он обозначается, как 365/365.

2. Обыкновенные проценты с точным числом дней ссуды. Этот метод, иногда называемый банковским, распространен в межстрановых ссудных операциях коммерческих банков. Он обозначается, как 365/360.

3. Обыкновенные проценты с приближенным числом дней ссуды. Такой метод применяется тогда, когда не требуется большой точности, например, при промежуточных расчетах. Он принят в практике коммерческих банков, условно этот метод обозначается как 360/360.

В кредитных отношениях иногда предусматриваются изменяющиеся во времени процентные ставки. Если это простые ставки, то наращенная на конец срока сумма определяется следующим образом:

FV = PV(1 + Σnt rt ),

где rt – ставка простых процентов в период t ; nt – продолжительность периода с постоянной ставкой, n = Σnt .

При расчете суммы простого процента в процессе дисконтирования стоимости денежных средств (т.е. суммы дисконта) используется формула:

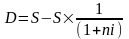
где D - сумма дисконта (по простым процентам) за обусловленный период инвестирования в целом;

S - конечная сумма вклада, обусловленная условиями инвестирования;

n - продолжительность инвестирования (в количестве периодов, по которым предусматривается расчет процентных платежей);

i - используемая дисконтная ставка, выраженная десятичной дробью.

Настоящая стоимость денежных средств (Р) с учетом рассчитанной суммы дисконта определяется по формуле:

Используемый в обоих случаях множитель 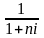называется дисконтным множителем (коэффициентом) простых процентов, значение которых всегда должно быть меньше единицы (коэффициент дисконтирования).

Приведем две формулы для определения неизвестных величин в различных случаях:

,

.
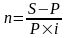