3. Расчётная часть задания

3.1 Оценка устойчивости сар частоты синхронного генератора

по критерию Гурвица

Постановка задачи.

Определить передаточную функцию разомкнутой системы; найти выражение характеристического уравнения замкнутой системы по формуле А(s)= В(s)+ D(s) = 0; определить численные значения коэффициентов а₃, а₂, а₁, а₀ этого уравнения, используя значения исходных параметров системы; оценить устойчивость САР по критерию Гурвица и определить критическое значение коэффициента передачи К_кр, при котором система находится на границе устойчивости.

Решение задачи.

- определение передаточной функции разомкнутой САР

- расчет параметров передаточной функции по исходным параметрам системы:

Значения исходных параметров

Постоянные параметры

f0=400 Гц

P=3

Варьируемые параметры

G=1 N=1

R_оу = 5000 + ( 1 + 0.1× 1)=5001.1

К_рк = 0.001 + 10^-3(0.1 ×1 + 0.01 ×1)=0.00111

К_р = 52.75 + 0.1(1 + 1)=52.95

w_р /w_у = 0.08 - 10^-2(1 + 0.1 ×1)=0.069

n = 5 + 0.01(1 + 1)=5.02

J = 0.04 + 10^-3(2 ×1 + 0.1 ×1)=0.0421

ρ = 0.1 + 10^-2( 1 + 0.1 ×1)=0.111

L_в = 4 + 0.01(1 + 1)=4.02

R_в = 200 + 0.1(2 ×1 + 1)=200.3

С_м1 = 34.12 + 0.01(2 ×1+ 1)=34.15

Значения параметров передаточных функций

К_иу= К_рк R_оу=5.551221

К_u= К_р w_р/w_у=3.65355

Т_му= n/ f₀=0.0126

К_u1= С_м1/ R_в ρ=1.535984

Т₁= J/ ρ=0.379279

Т₂= L_в/ R_в=0.0201

К_сг=Р/2π=0.477469

К = K_иу K_u K_u1 K_сг=5.551221×3.565355×1.535984×0.477469=14.8743

- нахождение выражения характеристического уравнения замкнутой САР

А(s) = В(s) + D(s) = (Т_му s+1) (Т₁ s+1) (Т₂ s+1) + К =

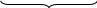
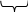= Т_му Т₁ Т₂ s³ +( Т_му Т₁₊ Т₁ Т₂+ Т₂ Т_му) s² +( Т_му + Т₁ +Т₂) s + 1 + К = 0.

а₃ а₂ а₁ а₀

- определение численных значений коэффициентов этого уравнения

а₃ = 0.0126×0.3793×0.0201=0.000096

а₂ = 0.0126×0.3793+0.3793×0.0201+0.0201×0.0126=0.012652

а₁ =0.0126+0.3793+0.0201 =0.412

а₀ = 1+14.8743=15.8743

- оценка устойчивости САР по критерию Гурвица

а₃ > 0; а₂ > 0; а₁ > 0; а₁ > 0 – необходимое условие устойчивости;

∆₂ = а₁а₂ – а₀а₃ =0.412×0.01265-15.8743×0.000096=0.003686 >0 – достаточное условие устойчивости.

Вывод: Система в замкнутом состоянии устойчива.

- определение значения K_кр. Из условия

∆₂ = а₁а₂ – а₀а₃ = а₁а₂–(1+К_кр) а₃=0,

при выполнении которого система находится на границе колебательной устойчивости, выразим K_кр

K_кр= ( a₁ а₂ - а₃)/ а₃ = (0.412×0.01265-0.000096)/0.000096=53.2896

3.2 Разработка схемы моделирования системы стабилизации частоты синхронного генератора в cреде MatLab

Рис.1 Схема моделирования ССЧ с числовыми значениями

в среде MatLab

Рис.2 Переходная характеристика ССЧ

Выводы по переходной характеристике:

-затухающий гармонический характер, то есть система устойчива;

f_уст=375

∆=0,05* f_уст=18,75 Гц

f_max=490 t_рег=0,26

ϐ= (f_макс- f_уст)/ f_уст*100%=30,67%

Построение логарифмических частотных характеристик

>> num1=[14.8743];

>> den1=[0.0126 1];

>> sys1=tf(num1,den1)

sys1 =

14.87

------------

0.0126 s + 1

Continuous-time transfer function.

>> num2=[1];

>> den2=[0.3793 1];

>> sys2=tf(num2,den2)

sys2 =

1

------------

0.3793 s + 1

Continuous-time transfer function.

>> num3=[1];

>> den3=[0.0201 1];

>> sys3=tf(num3,den3)

sys3 =

1

------------

0.0201 s + 1

Continuous-time transfer function.

>> sys=sys1*sys2*sys3

sys =

14.87

-----------------------------------------

9.606e-05 s^3 + 0.01266 s^2 + 0.412 s + 1

Continuous-time transfer function.

>> bode(sys)

Рис. 3 ЛЧХ ССЧ

Вывод: ω_с< ω_π , то есть система является устойчивой.