Методические рекомендации

1. Анализ и обработка ряда динамики

Вычислите цепные, базисные и средние показатели ряда динамики ввода в действие жилых домов строительной организацией. Произведите обработку ряда динамики способами

Динамика ввода в действие жилых домов строительной организацией

Год (номер по порядку)		Введено жилых домов, тыс. кв. м общей площади *
1	33.2
2	35.0
3	35.0
4	37.2
5	39.5
6	38.0
7	43.1
8	45.5
9	48.0
10		50.2

Методические рекомендации

После ознакомления с темой «Ряды динамики» для выполнения задания студенту предлагается:

1. Рассчитать цепные и базисные показатели абсолютного прироста, темпов роста и прироста, абсолютного значения 1% прироста ввода жилых домов, используя методику, приведенную в табл. 3.1:

Ряд динамики представляет собой ряд расположенных в хронологической последовательности числовых значений статистического показателя, характеризующих изменения общественных явлений во времени. Исходные данные подбираются за 8 – 10 лет.

Анализ ряда динамики предполагает расчет системы показателей (табл. 3)

1. Абсолютный прирост (Δy):

Δy_ц= y_i – у_{i - 1} – (цепной) (5)

Δy_б= y_i - у₀ - (базисный), (6)

где у_i – уровень сравниваемого периода;

у_{i - 1} – уровень предшествующего периода;

у₀ – уровень базисного периода.

2. Среднегодовой абсолютный прирост ( ) :

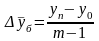
(7) или (8) ,

где n – число абсолютных приростов в изучаемом периоде;

m – число уровней ряда динамики в изучаемом периоде.

3. Темп роста (Тр):

у_i

Тр = ^________ · 100 (цепной) (9)

у_{i - 1}

у_i

Тр = ^_____ · 100 (базисный). (10)

У₀ ^____{___}

4. Среднегодовой темп роста (Тр)

^___ n _______________

Тр = √ Тр₁ · Тр₂ · … Тр_n , (11)

где n – число коэффициентов роста.

5. Темпы прироста (Тпр): Тпр = Тр – 100 (12)

6. Абсолютное значение 1% прироста (А%):

у_{i - 1}

А% = ^________ (13)

100

Таблица 3 - Показатели динамики

Годы	Уровни ряда	Абсолютный прирост			Темп роста %			Темп прироста %			Абсолютное значение 1% прирос-та А%
		цепной Δуц	базисный Δуб	цепной Трц		базисный Трб	цепной Тпрц		базисный Тпрб

3. Провести аналитическое выравнивание динамического ряда.

Наиболее точным способом выявления общей закономерности развития явления является аналитическое выравнивание по прямой.

Прямая линия выражается при помощи следующего уравнения:

ŷ_t = a₀ + a₁t , (14)

где ŷ_t – выравненные значения ряда;

t – время;

а₀ и а₁ – параметры искомой прямой;

Σy

а₀= ^______ (15)

n

Σyt

а₁= ^________ , (16)

Σt²

где у – фактические уровни ряда динамики;

n – число лет.

Уравнение решается по способу наименьших квадратов при котором

Σ (у_i - ŷ_t)² → min и Σt = 0

Если рассматриваемый период имеет нечетное число уровней, то условные обозначения времени примут следующий вид:

годы	1	2	3	4	5	6	7	8	9
t	-4	-3	-2	-1	0	+1	+2	+3	+4

Если рассматриваемый период имеет четное число уровней, то условные обозначения времени примут следующий вид:

годы	1	2	3	4	5	6	7	8	9	10
t	-9	-7	-5	-3	-1	+1	+3	+5	+7	+9

Следует знать, что если выравнивание выполнено правильно, то

Σу = Σŷ_t (табл. 4)

Таблица 4 - Аналитическое выравнивание

ряда динамики _____________

годы	Исход-ные уровни ряда дина- мики	Услов-ные обоз –наче-ния време-ни			Выровненный уровень ряда динамики	Откло-нение факти-ческих уровней от теорети-ческих	Квадраты отклоне-ний
	у	t	t2	уt	ŷt	у - ŷt	(у - ŷt)2

Для оценки степени приближения выравненных уравнений к фактическим данным рассчитывается остаточное среднее квадратическое отклонение и коэффициент вариации:

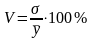σ_ост = ; (17) (18)