2.1.9 Гравітаційне поле. Закон всесвітнього тяжіння. Закон Кеплера. Інертна і гравітаційна маси. Принцип еквівалентності.

Закони Кеплера:1) кожна планета рухається по еліпсу, в одному з фокусів якого знаходить ся сонце; 2) радіус-вектори планет описують за однакові проміжки часу однакові площі; 3) квадрати періодів обертання планет навколо сонця відносяться як куби великих півосей їх орбіт.

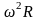За спрощення вважають орбіти коловими. Тоді із законів випливає сила, що сила діє на планети напрямлена вздовж радіуса кола, в центрі якого є сонце; сталими є кутова швидкість і прискорення планет , оскільки , то 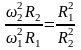оскільки прискорення пропорційне силі, то і це є сил всесвітнього тяжіння або гравітаційна сила (вага тіла). Гравітаційні властивості характеризує гравітаційна маса. Інертну масу визначають за прискоренням, якого набуває тіло під дією сили. Гравітаційну масу визначають так. Якщо до тіла підносити різні тіла, то на них діятиме різна сила тяжіння якщо гравітаційну масу тіла вибрати за 1, то масу іншого вважають в стільки раз більшою (або меншою), в скільки раз більшою (або меншою) сила його притягання до розглядуваного тіла. Отже кожне тіло можна характеризувати гравітаційною масою . Якщо відстань між тілами однакова, то , де – гравітаційна сила взаємодії між і . Відношення сили взаємодії двох тіл до добутку їх гравітаційних мас однакове для любої пари тіл і залежить лише від відстані між ними. Отже або враховуючи третій закон Ньютона Н*м²/кг² – гравітаційна стала. В 1798 р. Кавендіш виміряв сталу . Відхилення від закону помітні в точках, де зосереджені великі маси. Тоді необхідно користуватися теорією Ейнштейна. По своїй дії сили інерції не відрізняються від фундаментальних сил, які діють у гравітаційних полях. І коли ми визначаємо силу на основі закону всесвітнього тяжіння, то гравітаційна маса визначає прискорення, яке отримує точка при дії сили. І в загальному випадку інертна і гравітаційні маси однакові і їх не можливо розрізнити, а отже не можливо розрізнити сили тяжіння і сили інерції.

Принцип еквівалентності. Поле тяжіння у невеликій області простру і часу по своїй дії еквівалентні дії сил інерції в системі, що рухається з прискоренням.

2.1.10 Механічні коливання. Вільні і вимушені коливання. Резонанс. Коливання при наявності тертя.

Коливаннями називаються рухи, які тією чи іншою мірою повторюються у часі. Коливання називаються періодичними, якщо значення фізичних величин, які змінюються у процесі коливань, повторюються через рівні проміжки часу.

Періодом коливань Т називають проміжок часу протягом якого здійснюється одне повне коливання. Найпростішим видом періодичних коливань є гармонічні коливання – коливання які відбуваються за певним законом (найчастіше синусоїдальним): , де А – амплітуда коливань (максимальне відхилення від положення рівноваги), - фаза коливань, - початкова фаза коливань, - циклічна (кругова) частота.

Вільними називаються коливання, які виникають у системі в результаті якогось початкового відхилення системи від стану рівноваги, а зовнішні сили на неї не діють.

Вимушеними коливаннями називають коливання системи, які викликані дією на систему періодичних зовнішніх сил.

Резонанс – явище різкого зростання амплітуди вимушених коливань системи.

При терті.Будь-які реальні коливальні рухи відбуваються з поступовими втратами енергії коливальної системи на роботу проти сил тертя та на випром.,тобто на передавання енергії зовнішньому середовищу.Внаслідок цього амплітуда колив. з часом зменш. Такі колив. назив. затухаючими.

Р-ня механ. колив.,сила опору F_T пропорційна величині швидкості I і напрямлена завжди проти руху , де b-коеф.опору.

Отже на тіло крім квазіпружної сили діє сила опору.Р-ня динам. має вигляд (1)-це р-ня наз. диференц. р-ням затухаючих коливань. Розглянемо такі затухаючі колив.,коли періодичність руху зберігається. Р-ня руху тіла буде: (2). Встановимо характер зміни амплітуди затухаючих коливань з часом. Втрати енергії коливального руху тілом при затухаючих коливаннях визначаються роботою сил опору. За час dt втрати енергії (3). Перепишемо цей вираз так (4). Цю р-сть можна застосувати для визначення сер.втрат E за час одного періоду. Оскільки сер.знач. кінет.енргії коливального руху дорівнює половині його енергії, тобто k = ½ E, то співвідношення (4) можна записати 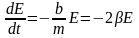(5), де , коеф. β назив. коеф. затухання. З (5) видно, що швидк. пропорційна самій енергії. Отримаємо (6), звідси отримаємо закон втрат енергії з часом (7). Оскільки повна енергія колив. руху пропорційна квадрату амплітуди, то з (7) маємо залежн. затух. колив. від часу (8). Врах. (8) р-ня (2) запишемо (9). Величини А₀ і φ визначаються як і для вільних колив. з початкових умов. Для визначення циклічної частоти ω або періоду Т затухаючих коливань треба знайти 1 і 2 похідні за часом від р-ня (9) і підставимо у (1) буде: (10), тоді 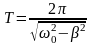(11), де - циклічна частота вільн. колив.

На рис.1 графік затух. колив. Знайдем віднош. двох амплітуд розділених у часі в один період (12). Звідси швидкість затухання коливань дорівнює (13). Замість логарифм. дикремента вводять величину, що наз. добротністю. (14) затухаючі колив. часто х-ють проміжок часу τ, протягом якого аплітуда колив. змінюється в е разів . Звідси і .

Для збільшення затухання коливань у техніці користуються пристроями, які наз. демпферами.

Рис. 1