23. Теорема Поста о полноте

Теорема Поста о функциональной полноте: система 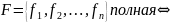она целиком не содержится ни в одном из пяти замкнутых классов (Поста): 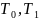, S, M, L.

Лемма : каждый класс Поста замкнут и не совпадает с

⊲(⇒):

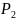
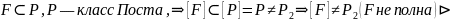
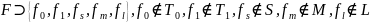
1. Покажем, что с помощью 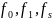можно получить 0 и 1

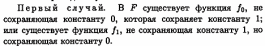
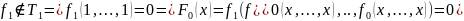
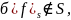
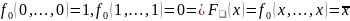Из самодвойственной ф-ии и отрицания можно получить константы (Лемма о несамодвойственной ф-ии)

2. С помощью 0, 1 и 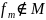можно получить отрицание (Лемма о немонотонной ф-ии)

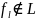3. С помощью 0,1, отрицания и можно получить x∧ y (Лемма о нелинейно ф-ии)

Таким образом ф-ия Функционально-Полной-Системы Q { x∧y,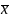 } может быть выражена формулой в базисе F , т.е. – F – ФПС (Функционально-Полная система)

24. Графы, ориентированные графы, связность, слабая связность, силь­ная связность, компоненты связности.

Неориентированный (ориентированный) граф G — это пара множеств , где V — конечное множество, элементы которого называют вершинами или узлами. E — множество неупорядоченных (упорядоченных) пар на V, т.е. подмножество множества двухэлементных подмножеств VV, элементы которого называют рёбрами (дугами). Для неориентированных графов степенью вершины v называют число dg(v) всех инцидентных (ребро инцидентно вершине, если она является одним из его концов) ей ребер. Для ориентированных графов полустепенью захода вершины v называется число 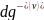заходящих в неё дуг, а полустепенью исхода v — число 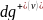исходящих из нее дуг. Степень вершины (ориентированный граф) v — это сумма полустепеней захода и исхода. Дуга называется инцидентной вершине , если она или заходит в v, или исходит из v. 

Неорграф (орграф) 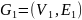называют подграфом неорграфа (орграфа) , если .

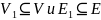Неорграф — ассоциированный с орграфом , если его множество вершин совпадает с множеством вершин орграфа G, а пара {u, v} образует ребро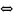 u≠v и из u в v или из v в u ведёт дуга, т.е. V1=V и .

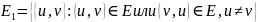Неорграф называют связным, если любые две его вершины u и v соединены цепью 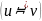. Орграф называют связным, если для .

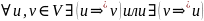Компонента связности графа — его максимально связный подграф.

Орграф слабосвязанный, если ассоциированный с ним неорграф связанный.

Орграф сильно связный, если в нём существует путь из любой вершины в любую другую. Бикомпонента орграфа — его максимальный сильно связный подграф.

25. Графы, изоморфизмы графов, группа автоморфизмов графа. Под­графы, пути, циклы, остовы, связный граф, количество остовных деревьев в связном графе.

Неорграф (орграф) называют подграфом неорграфа (орграфа) G =(V,E), если . Если V₁=V₂, то G₁ называется остовным подграфом графа G. Отображение 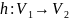множества вершин графа 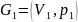в множество вершин графа 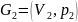называют изоморфизмом графа 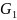в 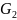, если любые две вершины смежны в первом графе тогда и только тогда, когда их образы смежны во втором графе, т.е. если . Группа автоморфизмов графа- множества всех автоморфизмов графа( - любая подстановка множества вершин, являющихся изоморфизмом G на себя). Цепь в неориентированном (путь в ориентированном) графе G — это последовательность вершин 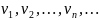, такая, что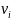 ⊢⊣ для 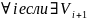. Простая цепь (все входящие в нее ребра попарно различны и все входящие в нее вершины, кроме, быть может, первой и последней, попарно различны) неориентированного (ориентированного) графа ненулевой длины с совпадающими концами называется циклом (контуром). Неориентированный (ориентированный) граф называют связным, если любые две его вершины соединены цепью (для любых его двух вершин u,v вершина u достижима из v или v достижима из u: u*v или v*u). Компонента неориентированного (ориентированного) графа G — его максимальный связный подграф. Диаметр графа D(G) – это расстояние между двумя наиболее удаленными друг от друга вершинами. Остовное дерево- ациклический связный подграф данного связного неориентированного графа, в который входят все его вершины.

Полный граф — граф, у которого каждая пара вершин соединена ребром.

Количество остовов в связном графе равно .

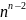Автоморфизм графа 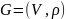— это любая подстановка множества его вершин, являющаяся изоморфизмом G на себя. Группой автоморфизмов называют подгруппу симметрической группы множества вершин графа, т.е. группу по операции композиции автоморфизмов.