17. Двойственная булева функция. Принцип двойственности ( теорема о суперпозиции), скнф.

Двойственной для булевой функции 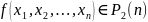называется булева функция

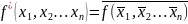
Принцип двойственности: функция, двойственная к суперпозиции функций, равна суперпозиции двойственных функций. Точнее:

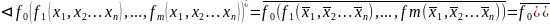
Функция называется самодвойственной, если .

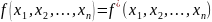Если мы применим принцип двойственности к СДНФ, то получим выражение:

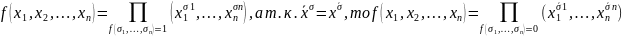
Полученное выражение является СКНФ.

Конъюнктивной нормальной формой (КНФ) называется конъюнкция простых дизъюнкций

Совершенная конъюнктивная нормальная форма, СКНФ — это такая КНФ, которая удовлетворяет условиям: 1)в ней нет одинаковых простых дизъюнкций 2)каждая простая дизъюнкция полная

18. Полиномы Жегалкина. Теорема о представлении булевой функции в виде полинома Жегалкина. Метод неопределенных коэффициентов

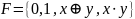– Базис Жигалкина

Полиномом Жегалкина-

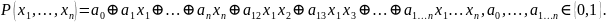
Теорема: Произвольную булеву функцию можно единственным образом представить в виде многочлена Жигалкина.

⊲Т.к. Базис Жигалкина – функционально полный, то каждая функция может быть представлена в виде многочлена Жигалкина. Поскольку число различных многочленов от n переменных . и совпадает с числом булевых функций от того же числа переменных, получается, что каждой булевой функции соответствует единственный многочлен ⊳

Метод неопределенных коэффициентов

Полином Жиаглкина имеет неизвестных коэффициентов.

Записываем ПЖ в общем виде, с неопределенными коэффициентами, выражаем значения ПЖ на фиксированных наборах через коэффиценты и приравнием его значению функции.

Получаем систему из простых уравнений в поле вычетов по модулю 2.

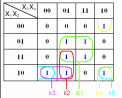
19. Задача о минимизации днф, сокращенные днф, алгоритм Блейка, карты Карно.

Задача о минимизации ДНФ сводится к отысканию такой формы, которая содержит наименьшее число литералов (функций х или 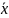) по сравнению с другими эквивалентными ей ДНФ.

D – множество всех ДНФ . D(f) – множество ДНФ предств. f. D=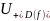

L : D 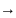R – мера сложности

Опр. Б.Ф. f

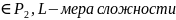
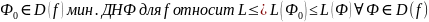
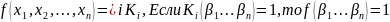
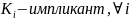
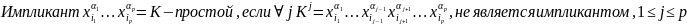
ДНФ, состоящая из всех простых импликант булевой функции f(x₁, …, x_n), называется сокращенной ДНФ этой функции.

Алгоритм Блейка является одним из методов склейки исходной функции и состоит в том, что к любой ДНФ, представляющей функцию применяются следующие тождества:

• Правило обобщенного склеивания:

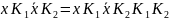
• Правило поглощения:

Сам алгоритм следующий: сначала к ДНФ применяют правило обобщенного склеивания до тех пор, пока не перестанут появляться новые элементарные конъюнкции, а затем, применяют правило поглощения. В результате получаем сокращённую ДНФ.

Карта Карно – прямоугольная таблица, являющаяся одной из форм таблицы истинности, с помощью которой быстро находятся простые импликанты. Карта Карно устроена так, что наборы, определяющие любые две соседние клетки, различаются в точности в одной позиции (т.е. различаются значениями ровно одной компоненты), причем клетки (одной и той же строки или одного и того же столбца), примыкающие к противоположным сторонам прямоугольника, также являются соседними в только что определенном смысле. Это можно представить себе так, что карта закручивается" в цилиндр" по обоим направлениям, т.е. в "тор".