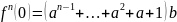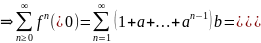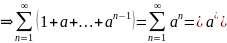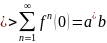- •4. Бинарные отношения: отношения эквивалентности, классы эквивалентности, теорема о разбиении на классы эквивалентности.
- •5. Бинарные отношения: отношения порядка, наибольший (наименьший) элемент, его единственность. Максимальный (минимальный) элемент, инфимум и супремум.
- •6. Равномощные множества. Счетные множества, их свойства. Пример бесконечного несчетного множества.
- •7. Теорема о мощности множества отображений из данного множества в двухэлементное.
- •8. Алгебраические системы: полугруппы, группы, подгруппы, группа перестановок, теорема Кэли.
- •9. Алгебраические системы: группы, подгруппы, циклическая группа, порядок элемента, теорема Лагранжа.
- •Обратный элемент:
- •11. Идемпотентные полукольца. Естественный порядок в идемпотентном полукольце. Супремум конечного множества и сумма его элементов.
- •12. Индуктивно упорядоченные множества. Монотонные отображения. Непрерывные отображения. Связь монотонности и непрерывности.
- •13. Индуктивно упорядоченные множества. Теорема о наименьшей неподвижной точке непрерывного отображения.
- •15. Булевы функции, способы задания, существенные и фиктивные переменные, отношение равенства, поиск существенных переменных.
- •16. Булевы функции, формулы над базисом функций, теорема о разложении, сднф.
- •17. Двойственная булева функция. Принцип двойственности ( теорема о суперпозиции), скнф.
- •18. Полиномы Жегалкина. Теорема о представлении булевой функции в виде полинома Жегалкина. Метод неопределенных коэффициентов
- •19. Задача о минимизации днф, сокращенные днф, алгоритм Блейка, карты Карно.
- •20. Задача о минимизации днф, тупиковые днф, их связь с минимальными днф, методы поиска тупиковых днф.
- •21. Замкнутые классы: классы функций, сохраняющих константу, класс самодвойственных функций, проверка их замкнутости, лемма о несамодвойственной функции.
- •22. Замкнутые классы: класс монотонных функций, класс линейных функций. Проверка замкнутости, лемма о немонотонной функции, лемма о нелинейной функции.
- •23. Теорема Поста о полноте
- •24. Графы, ориентированные графы, связность, слабая связность, сильная связность, компоненты связности.
- •25. Графы, изоморфизмы графов, группа автоморфизмов графа. Подграфы, пути, циклы, остовы, связный граф, количество остовных деревьев в связном графе.
- •26. Графы и матрицы: матрица смежности, её изменение при изменении нумерации вершин. Ранг графа. Проверка корректности определения ранга.
- •27. Деревья. Связь количества вершин и рёбер (неориентированного) дерева.
- •28. Взвешенный граф. Задача о минимальном остовном дереве в связном взвешенном графе. Алгоритм Краскала
- •29. Задача о достижимости в ориентированном графе. Связь матрицы достижимости и матрицы смежности.
- •30. Задача о кратчайшем пути в ориентированном взвешенном графе. Связь матрицы матрицы смежности (с весами) и матрицы стоимости кратчайших путей.
- •31. Алгоритм Дейкстры поиска кратчайшего пути во взвешенном ориентированном графе.
- •32. Алгоритм поиска в глубину в простом графе.
- •33. Алгоритм поиска в ширину в ориентированном графе.
- •34. Алфавит, слово, язык, множество языков над данным алфавитом, его мощность, операции над языками, полукольцо языков над данным алфавитом.
- •35. Регулярные операции и регулярные языки. Мощность множества регулярных языков. Образуют ли регулярные языки замкнутое полукольцо относительно регулярных операций?
- •36. Регулярные языки и автоматы распознаватели. Построение языка по автомату и автомата по языку. Теорема Клини.
- •37. Регулярные языки и автоматы—распознаватели. Поиск языка автомата распознавателя с помощью итерации матрицы смежности.
- •38. Лемма о разрастании для регулярных языков, пример нерегулярного языка.
- •39. Лемма о разрастании для регулярного языка, пример языка, не порождаемого автоматом—распознавателем.
- •40. Конечные детерминированные автоматы, способы задания, покрытия и морфизмы.
- •41. Конечные детерминированные автоматы, постановка задачи о минимизации, эквивалентные состояния, теорема о минимальном автомате.
- •43. Мощность множества языков, порожденных грамматиками. Существование языков, не порождаемых грамматиками.
- •44. Грамматики и автоматы-распознаватели. Место регулярных языков в Иерархии Хомского.
- •46. Задача распознавания в нк-грамматиках. Оценка высоты дерева вывода.
11. Идемпотентные полукольца. Естественный порядок в идемпотентном полукольце. Супремум конечного множества и сумма его элементов.
Полукольцо
— это
алгебра с двумя бинарными и двумя
нульарными операциями 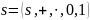 ,
такая, что для произвольных
элементов a,b,c множества S
выполняются следующие равенства,
называемые аксиомами полукольца:
,
такая, что для произвольных
элементов a,b,c множества S
выполняются следующие равенства,
называемые аксиомами полукольца:
(ассоциативность сложения);
(коммутативность сложения);
(0 — нейтральный элемент по сложению);
(ассоциативность умножения);
(1 — нейтральный элемент по умножению);
(дистрибутивность слева и справа)
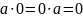
Идемпотентным
называется
полукольцо, в котором операция сложения
идемпотентна,
т.е
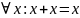
Естественный
порядок
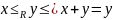
Лемма:
 упорядоченное
множество
упорядоченное
множество
◄рефлексивность, антисимметричность, транзитивность
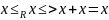
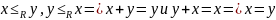


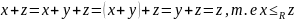
Теорема:
 - идемпотентное полукольцо. Если
Х — конечное подмножество (носителя)
идемпотентного полукольца, то sup
Х относительно естественного порядка
этого полукольца равен сумме всех
элементов множества Х, т.е
- идемпотентное полукольцо. Если
Х — конечное подмножество (носителя)
идемпотентного полукольца, то sup
Х относительно естественного порядка
этого полукольца равен сумме всех
элементов множества Х, т.е
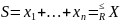
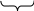
Доказательство:
1) S
– верхняя грань Х, т.е
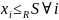
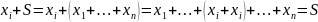
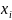
2)
Пусть М – верхняя грань =>
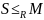
M
– верхняя грань
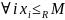
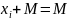

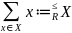
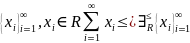
12. Индуктивно упорядоченные множества. Монотонные отображения. Непрерывные отображения. Связь монотонности и непрерывности.
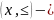 упорядоченное
множество
упорядоченное
множество
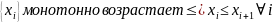
Множество вместе с заданным на нем отношением порядка называют упорядоченным множеством
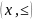 индуктивно
упорядочено, если
индуктивно
упорядочено, если
наименьший элемент последовательности
монотонная последовательность на
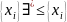
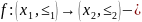 монотонно,
если
монотонно,
если

-
непрерывно, если
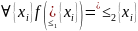
Теорема: Непрерывное отображение одного индуктивного упорядоченного множества в другое – монотонно
◄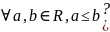

Образуем
последовательность
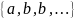 – монотонна
– монотонна

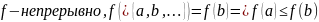
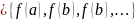 ►
►
13. Индуктивно упорядоченные множества. Теорема о наименьшей неподвижной точке непрерывного отображения.
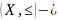 упорядоченное
множество
упорядоченное
множество
Множество вместе с заданным на нем отношением порядка называют упорядоченным множеством
индуктивно упорядочено, если
наименьший элемент последовательности
монотонная последовательность на
монотонно, если
- непрерывно, если
Теорема:
любое
непрерывное отображение f:
x->x
индуктивно упорядоченного множества
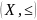 в себя имеет наименьшую неподвижную
точку, т.е
в себя имеет наименьшую неподвижную
точку, т.е
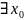 – неподвижная точка для f
– неподвижная точка для f
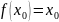
Доказательство:
Если 𝟘
– наименьший элемент в Х, то
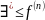 (𝟘)
– наименьшая неподвижная точка f.
(𝟘)
– наименьшая неподвижная точка f.
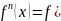
Лемма 0: Непрерывное отображение индуктивно упорядоченного множества монотонно
Лемма
1:
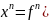 𝟘),
𝟘),
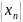 – монотонно возрастает
– монотонно возрастает
Лемма 2:
Л0 отображение непрерывно => монотонно
Л1
𝟘)
монотонно возрастает,
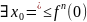
Лемма
3:
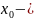 наименьшая
неподвижная точка
наименьшая
неподвижная точка
◄Пусть у – точка, неподвижная точка
𝟘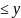 ,
𝟘
– наименьший элемент =>
,
𝟘
– наименьший элемент =>

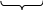
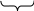
Если
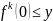 ,
,
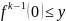 монотонно f
монотонно f
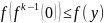
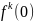 y
y
Т.е. у – верхняя грань
=>
последовательность
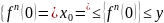
14. Замкнутые идемпотентные полукольца. Минимальное решение уравнения х = ах + b в замкнутом идемпотентном полукольце.
полукольцо, идемпотентно:
Замкнуто:
1)
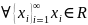
2)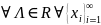
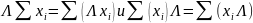
Наименьшее решение линейного уравнения в замкнутом полукольце:
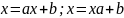
Теорема:
Наименьшими решениями уравнений выше
в замкнутых полукольцах являются
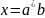 и
и
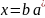 ,
где
,
где
 —
итерация элемента a.
—
итерация элемента a.
Доказательство:
◄По
теореме о наименьшей неподвижной точке
непрерывного отображения
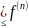 (𝟘)
= x,
записываем sup
как бесконечную сумму х =
(𝟘)
= x,
записываем sup
как бесконечную сумму х =
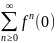

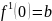
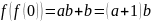
…