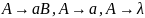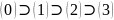- •4. Бинарные отношения: отношения эквивалентности, классы эквивалентности, теорема о разбиении на классы эквивалентности.
- •5. Бинарные отношения: отношения порядка, наибольший (наименьший) элемент, его единственность. Максимальный (минимальный) элемент, инфимум и супремум.
- •6. Равномощные множества. Счетные множества, их свойства. Пример бесконечного несчетного множества.
- •7. Теорема о мощности множества отображений из данного множества в двухэлементное.
- •8. Алгебраические системы: полугруппы, группы, подгруппы, группа перестановок, теорема Кэли.
- •9. Алгебраические системы: группы, подгруппы, циклическая группа, порядок элемента, теорема Лагранжа.
- •Обратный элемент:
- •11. Идемпотентные полукольца. Естественный порядок в идемпотентном полукольце. Супремум конечного множества и сумма его элементов.
- •12. Индуктивно упорядоченные множества. Монотонные отображения. Непрерывные отображения. Связь монотонности и непрерывности.
- •13. Индуктивно упорядоченные множества. Теорема о наименьшей неподвижной точке непрерывного отображения.
- •15. Булевы функции, способы задания, существенные и фиктивные переменные, отношение равенства, поиск существенных переменных.
- •16. Булевы функции, формулы над базисом функций, теорема о разложении, сднф.
- •17. Двойственная булева функция. Принцип двойственности ( теорема о суперпозиции), скнф.
- •18. Полиномы Жегалкина. Теорема о представлении булевой функции в виде полинома Жегалкина. Метод неопределенных коэффициентов
- •19. Задача о минимизации днф, сокращенные днф, алгоритм Блейка, карты Карно.
- •20. Задача о минимизации днф, тупиковые днф, их связь с минимальными днф, методы поиска тупиковых днф.
- •21. Замкнутые классы: классы функций, сохраняющих константу, класс самодвойственных функций, проверка их замкнутости, лемма о несамодвойственной функции.
- •22. Замкнутые классы: класс монотонных функций, класс линейных функций. Проверка замкнутости, лемма о немонотонной функции, лемма о нелинейной функции.
- •23. Теорема Поста о полноте
- •24. Графы, ориентированные графы, связность, слабая связность, сильная связность, компоненты связности.
- •25. Графы, изоморфизмы графов, группа автоморфизмов графа. Подграфы, пути, циклы, остовы, связный граф, количество остовных деревьев в связном графе.
- •26. Графы и матрицы: матрица смежности, её изменение при изменении нумерации вершин. Ранг графа. Проверка корректности определения ранга.
- •27. Деревья. Связь количества вершин и рёбер (неориентированного) дерева.
- •28. Взвешенный граф. Задача о минимальном остовном дереве в связном взвешенном графе. Алгоритм Краскала
- •29. Задача о достижимости в ориентированном графе. Связь матрицы достижимости и матрицы смежности.
- •30. Задача о кратчайшем пути в ориентированном взвешенном графе. Связь матрицы матрицы смежности (с весами) и матрицы стоимости кратчайших путей.
- •31. Алгоритм Дейкстры поиска кратчайшего пути во взвешенном ориентированном графе.
- •32. Алгоритм поиска в глубину в простом графе.
- •33. Алгоритм поиска в ширину в ориентированном графе.
- •34. Алфавит, слово, язык, множество языков над данным алфавитом, его мощность, операции над языками, полукольцо языков над данным алфавитом.
- •35. Регулярные операции и регулярные языки. Мощность множества регулярных языков. Образуют ли регулярные языки замкнутое полукольцо относительно регулярных операций?
- •36. Регулярные языки и автоматы распознаватели. Построение языка по автомату и автомата по языку. Теорема Клини.
- •37. Регулярные языки и автоматы—распознаватели. Поиск языка автомата распознавателя с помощью итерации матрицы смежности.
- •38. Лемма о разрастании для регулярных языков, пример нерегулярного языка.
- •39. Лемма о разрастании для регулярного языка, пример языка, не порождаемого автоматом—распознавателем.
- •40. Конечные детерминированные автоматы, способы задания, покрытия и морфизмы.
- •41. Конечные детерминированные автоматы, постановка задачи о минимизации, эквивалентные состояния, теорема о минимальном автомате.
- •43. Мощность множества языков, порожденных грамматиками. Существование языков, не порождаемых грамматиками.
- •44. Грамматики и автоматы-распознаватели. Место регулярных языков в Иерархии Хомского.
- •46. Задача распознавания в нк-грамматиках. Оценка высоты дерева вывода.
39. Лемма о разрастании для регулярного языка, пример языка, не порождаемого автоматом—распознавателем.
Пример нерегулярного языка.
L = L1*, где L1 = {anbn | n 0}. (стр. 541 Ткачев)
, к этому языку не применима лемма о разрастании.
Доказательство нерегулярности: Выберем достаточно большое и получим следующие варианты подцепочки v:
. Очевидно, что это целиком выведет за пределы языка, т.к. количество а растёт, а b — остаётся прежним.
. Аналогично.
. в данном случае возникнет вхождение подцепочки ba в слово, уже не принадлежащее нашему языку. Следовательно, язык L не регулярен.
(Язык
допускается КА тогда и только тогда,
когда он порождается регулярной
грамматикой). К языку
не применима лемма о разрастании.
Доказательство
приведено выше. Следовательно, в силу
своей нерегулярности,
 не порождается автоматом-распознавателем.
не порождается автоматом-распознавателем.
40. Конечные детерминированные автоматы, способы задания, покрытия и морфизмы.
Конечный
автомат называется детерминированным,
если в нем нет дуг с меткой λ и из любого
состояния по любому входному символу
возможен переход в точности в одно
состояние, т.е.
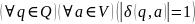
Конечный
автомат называется квазидетерминированным,
если в нем нет дуг с меткой λ и из любого
состояния по любому символу возможен
переход не более чем в одно состояние,
т.е.
Задание автомата:
Чтобы задать автомат, необходимо описать все его свойства (с помощью таблицы переходов и выходов, с помощью графа).
M
= (A,Z,S,q,f),
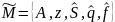
 покрывает
М, если существует ϕ: S->
покрывает
М, если существует ϕ: S-> ,
такое что
,
такое что
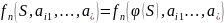
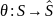 морфизм,
если что
морфизм,
если что
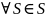 ,
что
,
что

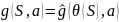
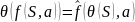
Утв. Существует морфизм – покрытие
Определение морфизма из Ткачева (не знаю, нужно или нет):
Пусть
V
и
W
–
некоторые алфавиты (в частности V
= W).
Морфизм
– это произвольное отображение
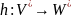 ,
такое, что h(
)
=
,
и
,
такое, что h(
)
=
,
и
(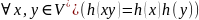
Иначе
говоря, морфизм – это гомоморфизм
свободного моноида
 в
свободный моноид
в
свободный моноид
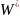 .
.
Морфизм h называется λ-свободным морфизмом, если для всякого слова
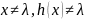 .
Если h:
.
Если h:
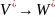 - морфизм, то соответствие h-1(обратное
к h)
из
в
называют инверсным
морфизмом.
- морфизм, то соответствие h-1(обратное
к h)
из
в
называют инверсным
морфизмом.
41. Конечные детерминированные автоматы, постановка задачи о минимизации, эквивалентные состояния, теорема о минимальном автомате.
Граф-автомат
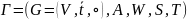 детерминизованный, если
детерминизованный, если
|S|=1
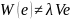
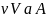 ребро
е с
началом в
v
и
W(
e) =
ребро
е с
началом в
v
и
W(
e) =
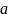 (с меткой
)
(с меткой
)
Дано: автомат М
Найти: минимизировать автомат, покрывающий данный
Опр.
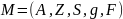
автомат
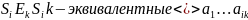
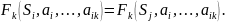

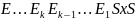
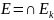
эквивалентн.
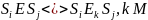
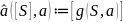
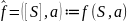

(Т) M/E –минимизированный автомат, покрывающий М
Лемма
1. 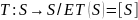 T-морфизм,
и, значит, покрытие
T-морфизм,
и, значит, покрытие
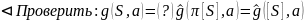 верно
по определению
верно
по определению
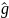
||
[f(S,a)]
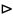
Лемма 1 => M/E покрывает М (осталось доказать, что min)
Лемма
0.
и
 корректно определены
корректно определены
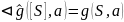
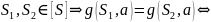
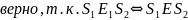
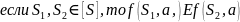
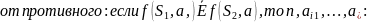
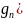
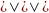
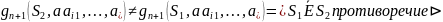
Лемма
2.
Пусть
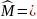 )
покрыв. М=(A,
Z,
S,
f,
g)
и
пусть |
)
покрыв. М=(A,
Z,
S,
f,
g)
и
пусть |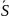 |
|S|,
то есть М
не минимизирован
|
|S|,
то есть М
не минимизирован
Тогда
E нетривиально на S,
то есть
неравное эквивалентное состояние:

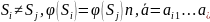
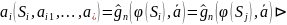
Лемма
3.
В автомате M/E
нет различных эквивалентных состояний
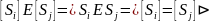
Вычисление
S/E 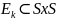
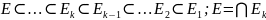


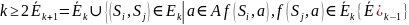
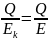
42.
Языки, порожденные грамматиками.
Иерархия Хомского.
(Иерархия
Хомского)
Порождающая
грамматика задается упорядоченной
четверкой G=(V,N,S,D),
где V
– алфавит, называемый терминальным, N
– алфавит, называемый нетерминальным,
причем V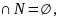
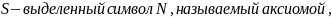
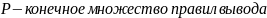

Язык,
порождаемый грамматикой G,
это множество L(G)
всех выводимых из аксиом грамматик
терминальных цепочек
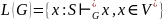
Иерархия Хомского — классификация формальных языков и формальных грамматик, согласно которой они делятся на 4 типа по их условной сложности. Регулярные языки порождаются регулярными грамматиками, которые, будучи частным случаем праволинейных грамматик, относятся к «наименьшему» типу грамматик в иерархии Хомского.
Сложность языка определяется его типом. Наиболее сложные — языки с фразовой структурой (сюда можно отнести естественные языки), далее — КЗ-, КС-языки и самые простые — регулярные языки.
Иерархия Хомского
произвольная грамматика порожд. рекурсивно – перечисляемые языки
контекстно-зависимые грамматики и языки все продукции имеют вид
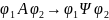
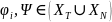
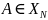
контекстно-свободные
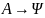
регулярные (правильная) грам.