
- •4. Бинарные отношения: отношения эквивалентности, классы эквивалентности, теорема о разбиении на классы эквивалентности.
- •5. Бинарные отношения: отношения порядка, наибольший (наименьший) элемент, его единственность. Максимальный (минимальный) элемент, инфимум и супремум.
- •6. Равномощные множества. Счетные множества, их свойства. Пример бесконечного несчетного множества.
- •7. Теорема о мощности множества отображений из данного множества в двухэлементное.
- •8. Алгебраические системы: полугруппы, группы, подгруппы, группа перестановок, теорема Кэли.
- •9. Алгебраические системы: группы, подгруппы, циклическая группа, порядок элемента, теорема Лагранжа.
- •Обратный элемент:
- •11. Идемпотентные полукольца. Естественный порядок в идемпотентном полукольце. Супремум конечного множества и сумма его элементов.
- •12. Индуктивно упорядоченные множества. Монотонные отображения. Непрерывные отображения. Связь монотонности и непрерывности.
- •13. Индуктивно упорядоченные множества. Теорема о наименьшей неподвижной точке непрерывного отображения.
- •15. Булевы функции, способы задания, существенные и фиктивные переменные, отношение равенства, поиск существенных переменных.
- •16. Булевы функции, формулы над базисом функций, теорема о разложении, сднф.
- •17. Двойственная булева функция. Принцип двойственности ( теорема о суперпозиции), скнф.
- •18. Полиномы Жегалкина. Теорема о представлении булевой функции в виде полинома Жегалкина. Метод неопределенных коэффициентов
- •19. Задача о минимизации днф, сокращенные днф, алгоритм Блейка, карты Карно.
- •20. Задача о минимизации днф, тупиковые днф, их связь с минимальными днф, методы поиска тупиковых днф.
- •21. Замкнутые классы: классы функций, сохраняющих константу, класс самодвойственных функций, проверка их замкнутости, лемма о несамодвойственной функции.
- •22. Замкнутые классы: класс монотонных функций, класс линейных функций. Проверка замкнутости, лемма о немонотонной функции, лемма о нелинейной функции.
- •23. Теорема Поста о полноте
- •24. Графы, ориентированные графы, связность, слабая связность, сильная связность, компоненты связности.
- •25. Графы, изоморфизмы графов, группа автоморфизмов графа. Подграфы, пути, циклы, остовы, связный граф, количество остовных деревьев в связном графе.
- •26. Графы и матрицы: матрица смежности, её изменение при изменении нумерации вершин. Ранг графа. Проверка корректности определения ранга.
- •27. Деревья. Связь количества вершин и рёбер (неориентированного) дерева.
- •28. Взвешенный граф. Задача о минимальном остовном дереве в связном взвешенном графе. Алгоритм Краскала
- •29. Задача о достижимости в ориентированном графе. Связь матрицы достижимости и матрицы смежности.
- •30. Задача о кратчайшем пути в ориентированном взвешенном графе. Связь матрицы матрицы смежности (с весами) и матрицы стоимости кратчайших путей.
- •31. Алгоритм Дейкстры поиска кратчайшего пути во взвешенном ориентированном графе.
- •32. Алгоритм поиска в глубину в простом графе.
- •33. Алгоритм поиска в ширину в ориентированном графе.
- •34. Алфавит, слово, язык, множество языков над данным алфавитом, его мощность, операции над языками, полукольцо языков над данным алфавитом.
- •35. Регулярные операции и регулярные языки. Мощность множества регулярных языков. Образуют ли регулярные языки замкнутое полукольцо относительно регулярных операций?
- •36. Регулярные языки и автоматы распознаватели. Построение языка по автомату и автомата по языку. Теорема Клини.
- •37. Регулярные языки и автоматы—распознаватели. Поиск языка автомата распознавателя с помощью итерации матрицы смежности.
- •38. Лемма о разрастании для регулярных языков, пример нерегулярного языка.
- •39. Лемма о разрастании для регулярного языка, пример языка, не порождаемого автоматом—распознавателем.
- •40. Конечные детерминированные автоматы, способы задания, покрытия и морфизмы.
- •41. Конечные детерминированные автоматы, постановка задачи о минимизации, эквивалентные состояния, теорема о минимальном автомате.
- •43. Мощность множества языков, порожденных грамматиками. Существование языков, не порождаемых грамматиками.
- •44. Грамматики и автоматы-распознаватели. Место регулярных языков в Иерархии Хомского.
- •46. Задача распознавания в нк-грамматиках. Оценка высоты дерева вывода.
37. Регулярные языки и автоматы—распознаватели. Поиск языка автомата распознавателя с помощью итерации матрицы смежности.
Регулярные языки порождаются регулярными грамматиками, для которых АаВ или Аа, где а — либо терминал, либо пустая цепочка (В — нетерминал).
Множество регулярных языков равномощно множеству натуральных чисел, т.е. оно счётное.
Автоматом-распознавателем называется упорядоченная четвёрка , где — ориентированный мультиграф, S — входы, а T — выходы.
Для
поиска
языка автомата достаточно
вычислить матрицу стоимостей автомата.
Вычислим итерации с помощью систем
линейных уравнений. Нам понадобится
решить n
= |Q|
систем вида Ej
= AEj
+ εj,
где А
– квадратная матрица n-го
порядка, элемент aij
которой является регулярным выражением,
служащим меткой дуги из вершины qi
в вершину qj,
если такая дуга существует, и равен
регулярному выражению
 ,
если нет такой дуги; Ej
– j-й
столбец единичной матрицы, т.е. столбец,
у которого все компоненты, кроме j-й,
равны
(нулю полукольца R(V)),
а j-я
компонента равна λ (единице полукольца
R(V)).
Решив указанные n
систем, найдем матрицу стоимостей C
= A*
заданного конечного автомата. Но нам
нужна не вся матрица стоимостей, а
только элементы вида cst,
где s
– номер начального, а t
– один из номеров заключительного
состояния. Поэтому, вместо того чтобы
решать несколько систем линейных
уравнений, достаточно решить одну: E
= AE
+
β, где β – столбец, все компоненты
которого равны
(нулю полукольца R(V)),
кроме компонент с номерами t1,…,tm,
которые являются номерами заключительных
состояний. Эти компоненты равны λ
(единице полукольца R(V)).
Другими словами, ко всем компонентам
системы, соответствующим заключительным
состояниям, добавляется слагаемое λ.
,
если нет такой дуги; Ej
– j-й
столбец единичной матрицы, т.е. столбец,
у которого все компоненты, кроме j-й,
равны
(нулю полукольца R(V)),
а j-я
компонента равна λ (единице полукольца
R(V)).
Решив указанные n
систем, найдем матрицу стоимостей C
= A*
заданного конечного автомата. Но нам
нужна не вся матрица стоимостей, а
только элементы вида cst,
где s
– номер начального, а t
– один из номеров заключительного
состояния. Поэтому, вместо того чтобы
решать несколько систем линейных
уравнений, достаточно решить одну: E
= AE
+
β, где β – столбец, все компоненты
которого равны
(нулю полукольца R(V)),
кроме компонент с номерами t1,…,tm,
которые являются номерами заключительных
состояний. Эти компоненты равны λ
(единице полукольца R(V)).
Другими словами, ко всем компонентам
системы, соответствующим заключительным
состояниям, добавляется слагаемое λ.
Решение системы будет иметь вид: E = A* β = A* , …, , λ, , …, , λ, , …, )T
(Элементы λ находятся в строках с номерами t1, …, tm). В этой формуле, умножая матрицу А*, равную матрице С стоимостей, на столбец β, получим столбец, s-я компонента которого xs будет равна произведению s-й строки матрицы С (cs1, …, cst1, …, cstm, …, csn) на столбец β в этой формуле, т.е. xs = cst1 + … + cstm. Это и есть регулярное выражение, обозначающее язык конечного автомата.
38. Лемма о разрастании для регулярных языков, пример нерегулярного языка.
Лемма о разрастании регулярных языков утверждает, что любой регулярный язык допускает представление всех своих достаточно длинных цепочек в виде соединения трех цепочек, причем средняя цепочка из этих трех не пуста, ограничена по длине, и ее “накачка” – повторение любое число раз – или выбрасывание не выводит за пределы языка (т.е. дает цепочки, принадлежащие данному регулярному языку).
Лемма:
Если L
– регулярный язык, то существует
натуральная константа kL
(зависящая от L),
такая что для любой цепочки x
L,
длина которой не меньше kL,
x
допускает представление в виде x
= uvw,
где v
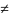 λ и |v|
λ и |v|
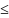 kL,
причем для любого n
kL,
причем для любого n
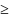 0
цепочка xn
=
uvnw
L.
0
цепочка xn
=
uvnw
L.
Док-во:
Поскольку
язык L
регулярен, то, согласно теореме Клини,
существует конечный автомат M
= (V,
Q,
q0,
F,
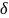 ),
допускающий его, т.е. L
= L(M).
Положив kL
= |Q|,
т.е. введя константу kL
как число состояний конечного автомата
М, фиксируем произвольно цепочку x
L,
длина l
которой не меньше kL.
Так как l
> 0,
то цепочка x
не является пустой, и мы можем положить
x
= x(1)…x(l),
l
> 0.
),
допускающий его, т.е. L
= L(M).
Положив kL
= |Q|,
т.е. введя константу kL
как число состояний конечного автомата
М, фиксируем произвольно цепочку x
L,
длина l
которой не меньше kL.
Так как l
> 0,
то цепочка x
не является пустой, и мы можем положить
x
= x(1)…x(l),
l
> 0.
С![]() огласно
теореме о детерминизации, автомат M
является детерминированным, следовательно,
существует единственный путь, ведущий
из начального состояния q0
в одно из заключительных состояний qf,
на котором читается x.
огласно
теореме о детерминизации, автомат M
является детерминированным, следовательно,
существует единственный путь, ведущий
из начального состояния q0
в одно из заключительных состояний qf,
на котором читается x.
Так
как длина l
цепочки x
не меньше числа состояний M,
то есть числа всех вершин графа M,
то, поскольку число вершин в любом пути
ровно на единицу больше числа дуг в
этом пути (т.е. длины пути), число вершин
в рассмотренном выше пути будет больше,
чем число всех вершин графа. Это значит,
что хотя бы одна из вершин данного пути
повторяется и она, таким образом,
содержится в некотором контуре.
Обозначим
эту вершину через p.
Тогда путь, несущий цепочку x,
разбивается на три части: 1) путь из q0
в p;
2) контур, проходящий через p;
3) путь из p
в qf.
Обозначим через u цепочку, читаемую на первой части пути, через v – цепочку, читаемую на контуре, а через w - цепочку, читаемую на третьей части, получим x = uvw, причем поскольку любой контур есть простой путь, то |v| kL (длина простого пути не может быть больше, чем число вершин графа) и v λ, так как контур имеет ненулевую длину. Но теперь совершенно очевидно, что контур можно пройти любое число n раз или ни разу. В первом случае на этом пути будет прочитана цепочка uvnw при n > 0, а во втором цепочка uw. Таким образом, любая цепочка xn = uvnw (n 0) содержится в языке L.
Пример нерегулярного языка.
L = L1*, где L1 = {anbn | n 0}. (стр. 541 Ткачев)
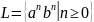 ,
к этому языку не применима лемма о
разрастании.
,
к этому языку не применима лемма о
разрастании.
Доказательство
нерегулярности:
Выберем достаточно большое
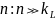 и получим следующие варианты подцепочки
v:
и получим следующие варианты подцепочки
v:
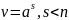 .
Очевидно, что это целиком выведет за
пределы языка, т.к. количество а
растёт, а b
—
остаётся прежним.
.
Очевидно, что это целиком выведет за
пределы языка, т.к. количество а
растёт, а b
—
остаётся прежним.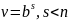 .
Аналогично.
.
Аналогично.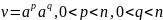 .
в данном случае возникнет вхождение
подцепочки ba
в слово, уже не принадлежащее нашему
языку. Следовательно, язык L
не регулярен
.
в данном случае возникнет вхождение
подцепочки ba
в слово, уже не принадлежащее нашему
языку. Следовательно, язык L
не регулярен
