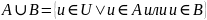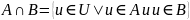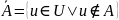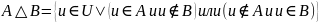- •4. Бинарные отношения: отношения эквивалентности, классы эквивалентности, теорема о разбиении на классы эквивалентности.
- •5. Бинарные отношения: отношения порядка, наибольший (наименьший) элемент, его единственность. Максимальный (минимальный) элемент, инфимум и супремум.
- •6. Равномощные множества. Счетные множества, их свойства. Пример бесконечного несчетного множества.
- •7. Теорема о мощности множества отображений из данного множества в двухэлементное.
- •8. Алгебраические системы: полугруппы, группы, подгруппы, группа перестановок, теорема Кэли.
- •9. Алгебраические системы: группы, подгруппы, циклическая группа, порядок элемента, теорема Лагранжа.
- •Обратный элемент:
- •11. Идемпотентные полукольца. Естественный порядок в идемпотентном полукольце. Супремум конечного множества и сумма его элементов.
- •12. Индуктивно упорядоченные множества. Монотонные отображения. Непрерывные отображения. Связь монотонности и непрерывности.
- •13. Индуктивно упорядоченные множества. Теорема о наименьшей неподвижной точке непрерывного отображения.
- •15. Булевы функции, способы задания, существенные и фиктивные переменные, отношение равенства, поиск существенных переменных.
- •16. Булевы функции, формулы над базисом функций, теорема о разложении, сднф.
- •17. Двойственная булева функция. Принцип двойственности ( теорема о суперпозиции), скнф.
- •18. Полиномы Жегалкина. Теорема о представлении булевой функции в виде полинома Жегалкина. Метод неопределенных коэффициентов
- •19. Задача о минимизации днф, сокращенные днф, алгоритм Блейка, карты Карно.
- •20. Задача о минимизации днф, тупиковые днф, их связь с минимальными днф, методы поиска тупиковых днф.
- •21. Замкнутые классы: классы функций, сохраняющих константу, класс самодвойственных функций, проверка их замкнутости, лемма о несамодвойственной функции.
- •22. Замкнутые классы: класс монотонных функций, класс линейных функций. Проверка замкнутости, лемма о немонотонной функции, лемма о нелинейной функции.
- •23. Теорема Поста о полноте
- •24. Графы, ориентированные графы, связность, слабая связность, сильная связность, компоненты связности.
- •25. Графы, изоморфизмы графов, группа автоморфизмов графа. Подграфы, пути, циклы, остовы, связный граф, количество остовных деревьев в связном графе.
- •26. Графы и матрицы: матрица смежности, её изменение при изменении нумерации вершин. Ранг графа. Проверка корректности определения ранга.
- •27. Деревья. Связь количества вершин и рёбер (неориентированного) дерева.
- •28. Взвешенный граф. Задача о минимальном остовном дереве в связном взвешенном графе. Алгоритм Краскала
- •29. Задача о достижимости в ориентированном графе. Связь матрицы достижимости и матрицы смежности.
- •30. Задача о кратчайшем пути в ориентированном взвешенном графе. Связь матрицы матрицы смежности (с весами) и матрицы стоимости кратчайших путей.
- •31. Алгоритм Дейкстры поиска кратчайшего пути во взвешенном ориентированном графе.
- •32. Алгоритм поиска в глубину в простом графе.
- •33. Алгоритм поиска в ширину в ориентированном графе.
- •34. Алфавит, слово, язык, множество языков над данным алфавитом, его мощность, операции над языками, полукольцо языков над данным алфавитом.
- •35. Регулярные операции и регулярные языки. Мощность множества регулярных языков. Образуют ли регулярные языки замкнутое полукольцо относительно регулярных операций?
- •36. Регулярные языки и автоматы распознаватели. Построение языка по автомату и автомата по языку. Теорема Клини.
- •37. Регулярные языки и автоматы—распознаватели. Поиск языка автомата распознавателя с помощью итерации матрицы смежности.
- •38. Лемма о разрастании для регулярных языков, пример нерегулярного языка.
- •39. Лемма о разрастании для регулярного языка, пример языка, не порождаемого автоматом—распознавателем.
- •40. Конечные детерминированные автоматы, способы задания, покрытия и морфизмы.
- •41. Конечные детерминированные автоматы, постановка задачи о минимизации, эквивалентные состояния, теорема о минимальном автомате.
- •43. Мощность множества языков, порожденных грамматиками. Существование языков, не порождаемых грамматиками.
- •44. Грамматики и автоматы-распознаватели. Место регулярных языков в Иерархии Хомского.
- •46. Задача распознавания в нк-грамматиках. Оценка высоты дерева вывода.
Оглавление
7. Теорема о мощности множества отображений из данного множества в двухэлементное. 9
8. Алгебраические системы: полугруппы, группы, подгруппы, группа перестановок, теорема Кэли. 10
9. Алгебраические системы: группы, подгруппы, циклическая группа, порядок элемента, теорема Лагранжа. 11
10. Алгебраические системы: кольца, поля, делители нуля, доказательство того, что конечное коммутативное кольцо с отличной от нуля единицей и без делителей нуля является полем, примеры конечных полей. 12
11. Идемпотентные полукольца. Естественный порядок в идемпотентном полукольце. Супремум конечного множества и сумма его элементов. 13
12. Индуктивно упорядоченные множества. Монотонные отображения. Непрерывные отображения. Связь монотонности и непрерывности. 14
13. Индуктивно упорядоченные множества. Теорема о наименьшей неподвижной точке непрерывного отображения. 15
14. Замкнутые идемпотентные полукольца. Минимальное решение уравнения х = ах + b в замкнутом идемпотентном полукольце. 16
15. Булевы функции, способы задания, существенные и фиктивные переменные, отношение равенства, поиск существенных переменных. 17
16. Булевы функции, формулы над базисом функций, теорема о разложении, СДНФ. 19
17. Двойственная булева функция. Принцип двойственности ( теорема о суперпозиции), СКНФ. 20
18. Полиномы Жегалкина. Теорема о представлении булевой функции в виде полинома Жегалкина. Метод неопределенных коэффициентов 21
19. Задача о минимизации ДНФ, сокращенные ДНФ, алгоритм Блейка, карты Карно. 22
20. Задача о минимизации ДНФ, тупиковые ДНФ, их связь с минимальными ДНФ, методы поиска тупиковых ДНФ. 23
21. Замкнутые классы: классы функций, сохраняющих константу, класс самодвойственных функций, проверка их замкнутости, лемма о несамодвойственной функции. 24
22. Замкнутые классы: класс монотонных функций, класс линейных функций. Проверка замкнутости, лемма о немонотонной функции, лемма о нелинейной функции. 25
23. Теорема Поста о полноте 27
24. Графы, ориентированные графы, связность, слабая связность, сильная связность, компоненты связности. 28
25. Графы, изоморфизмы графов, группа автоморфизмов графа. Подграфы, пути, циклы, остовы, связный граф, количество остовных деревьев в связном графе. 29
26. Графы и матрицы: матрица смежности, её изменение при изменении нумерации вершин. Ранг графа. Проверка корректности определения ранга. 30
27. Деревья. Связь количества вершин и рёбер (неориентированного) дерева. 31
28. Взвешенный граф. Задача о минимальном остовном дереве в связном взвешенном графе. Алгоритм Краскала 32
29. Задача о достижимости в ориентированном графе. Связь матрицы достижимости и матрицы смежности. 33
30. Задача о кратчайшем пути в ориентированном взвешенном графе. Связь матрицы матрицы смежности (с весами) и матрицы стоимости кратчайших путей. 34
31. Алгоритм Дейкстры поиска кратчайшего пути во взвешенном ориентированном графе. 35
32. Алгоритм поиска в глубину в простом графе. 36
33. Алгоритм поиска в ширину в ориентированном графе. 37
34. Алфавит, слово, язык, множество языков над данным алфавитом, его мощность, операции над языками, полукольцо языков над данным алфавитом. 38
35. Регулярные операции и регулярные языки. Мощность множества регулярных языков. Образуют ли регулярные языки замкнутое полукольцо относительно регулярных операций? 39
36. Регулярные языки и автоматы распознаватели. Построение языка по автомату и автомата по языку. Теорема Клини. 40
41. Конечные детерминированные автоматы, постановка задачи о минимизации, эквивалентные состояния, теорема о минимальном автомате. 46
43. Мощность множества языков, порожденных грамматиками. Существование языков, не порождаемых грамматиками. 49
44. Грамматики и автоматы-распознаватели. Место регулярных языков в Иерархии Хомского. 50
45. НК-грамматики. Языки, порожденные НК-грамматиками в иерархии Хомского. 51
46. Задача распознавания в НК-грамматиках. Оценка высоты дерева вывода. 52
Равенство множеств, операции над множествами, их свойства: ассоциативность, коммутативность, дистрибутивность, идемпотентность, законы поглощения и законы де Моргана. Доказательство последних методом характеристических функций.
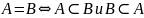 или
или
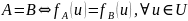
Операции (на подмножествах универсального множества U).
Свойства:
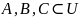
Ассоциативность:
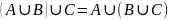 или
или
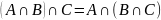 или
или
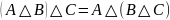
Коммутативность:
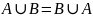 или
или
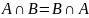 или
или

Дистрибутивность:
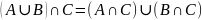 или
или
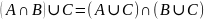
Идемпотентность:
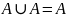 или
или
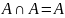
Закон поглощения:
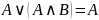 или
или

Закон де Моргана:
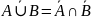 или
или
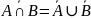
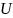 – универсальное
множество.
– универсальное
множество.
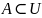 .
Характеристическая функция
.
Характеристическая функция
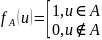
Доказательство:
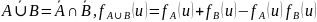
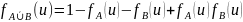
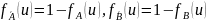
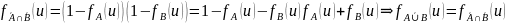
,
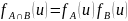
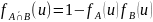
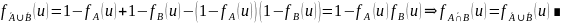
2.
Отображения множеств, характеристическая
функция множества.
Свойства характеристических функций
(связь с элементарными операциями).
Характеристическая функция симметрической
разности.
X,
Y
– множества.
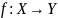 – отображение,
– отображение,
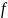 – закон, по которому
– закон, по которому
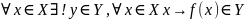 .
U
– универсальное множество.
.
U
– универсальное множество.
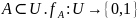 – отображение, характеристическая
функция.
Свойства:
1)
– отображение, характеристическая
функция.
Свойства:
1)
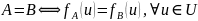 2)
3)
2)
3)
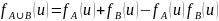 4)
4)
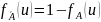 5)
5)
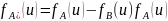 6)
6)
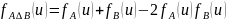 Доказательство:
Доказательство:
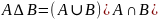
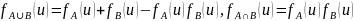
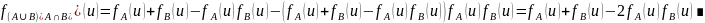
3. Понятие отображения множеств. Сюръективные, инъективные и биективные отображения. Композиция отображений. Ассоциативность композиции. Обратное отображение. Теорема существования обратного отображения. Отображение, обратное к композиции отображений.
X,
Y
– множества.
– отображение,
– закон, по которому
– образ элемента
 .
.
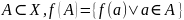 – образ
множества.
– образ
множества.
– сюръективное

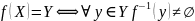
– инъективное
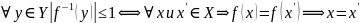
– биективно инъективное и сюръективное
Композиция
отображений
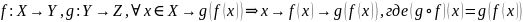 Ассоциативность
композиции
Ассоциативность
композиции
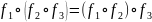
Доказательство:
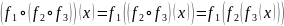
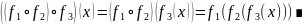 Обратное
отображение
Обратное
отображение
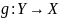 обратное
к
,
если
обратное
к
,
если
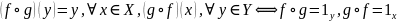
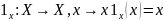 – тождественное отображение
– тождественное отображение
Теорема существования обратного отображения
– обратимо
(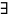 обратное к нему)
биективно
обратное к нему)
биективно
Доказательство:
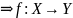 обратимо.
обратимо.
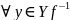 – обратное отображение
– обратное отображение
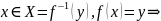 сюръекция
сюръекция
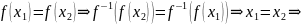 инъекция
инъекция
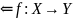 биекция.
биекция.
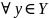 сюръекция
сюръекция
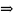
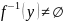 ,
инъекция
,
инъекция
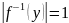 ,
т.к.
,
т.к.
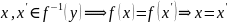
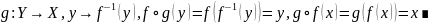 Отображение,
обратное к композиции отображений
Отображение,
обратное к композиции отображений
 .
.
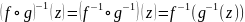
4. Бинарные отношения: отношения эквивалентности, классы эквивалентности, теорема о разбиении на классы эквивалентности.
Бинарное
отношение
на X
и Y
– это
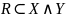 .
.
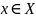 находится в отношении R
к
находится в отношении R
к
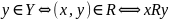 .
.
 – отношение эквивалентности, если оно
рефлексивно, симметрично, транзитивно.
– отношение эквивалентности, если оно
рефлексивно, симметрично, транзитивно.
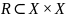 рефлексивно,
если
рефлексивно,
если
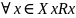 .
.– симметрично,
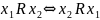 .
.– транзитивно,
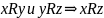 .
.
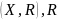 – отношение
эквивалентности.
– отношение
эквивалентности.
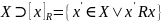 – класс эквивалентности элемента
.
– класс эквивалентности элемента
.
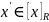 – представитель класса
– представитель класса
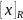 .
.
Теорема о разбиении на классы эквивалентности.
R – отношение эквивалентности на X, тогда все различные классы эквивалентности – разбиение множества X (т.е. не пусты, не пересекаются и их объединение = X).
Пусть
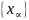 – разбиения множества X,
тогда
отношение эквивалентности R
на X.
– разбиения множества X,
тогда
отношение эквивалентности R
на X.
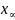 - классы эквивалентности на R.
- классы эквивалентности на R.
Доказательство:
1)
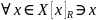 (рефлексивность).
(рефлексивность).
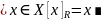 .
.
Лемма
1.
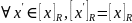 .
.
Доказательство:
1)
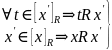 транзитивность
транзитивность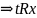 ,
т.е.
,
т.е.
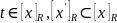 .
.
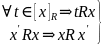 транзитивность
транзитивность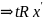 ,
т.е.
,
т.е.
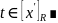
Лемма
2.
Если
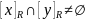 ,
то
,
то
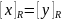 .
.
Доказательство:
1)
 .
Лемма 1
.
Лемма 1
 .
2)
.
2)
 .
.
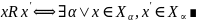
Лемма
3.
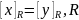 – отношение эквивалентности.
– отношение эквивалентности.
Доказательство:
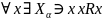 .
Симметричность:
.
Симметричность:
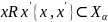 .
Транзитивность:
.
Транзитивность:
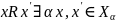 ;
;
 ;
;
 не пусто
не пусто
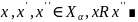
Лемма
4.
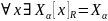
Доказательство:
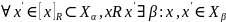 .
.
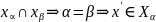 ,
т.е.
,
т.е.
 .
.
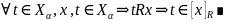
5. Бинарные отношения: отношения порядка, наибольший (наименьший) элемент, его единственность. Максимальный (минимальный) элемент, инфимум и супремум.
Бинарное отношение на X и Y – это . находится в отношении R к .
– отношение порядка, если оно рефлексивно, антисимметрично, транзитивно.
рефлексивно, если .
– антисимметрично,
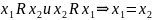 .
.– транзитивно, .
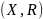 – упорядоченное множество.
– упорядоченное множество.
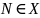 наибольший,
если
наибольший,
если

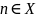 наименьший,
если
наименьший,
если
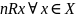
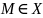 максимальный,
если
максимальный,
если
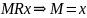
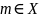 минимальный,
если
минимальный,
если
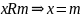
Теорема. Если наибольший (наименьший) элемент, то он единственен.
Доказательство:
(от противного)
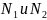 – наибольшие элементы.
– наибольшие элементы.
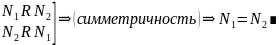
– упорядоченное множество.
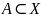 .
– верхняя грань для A,
если
.
– верхняя грань для A,
если
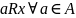 .
.
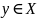 – нижняя грань для A,
если
– нижняя грань для A,
если
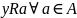 .
.
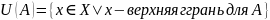 .
.
 – упорядоченное множество. Наименьший
элемент
– упорядоченное множество. Наименьший
элемент
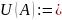 наименьшая (точная) верхняя грань =
наименьшая (точная) верхняя грань =
 .
.
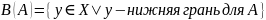 .
Наибольший элемент множества
.
Наибольший элемент множества
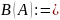 наибольшая
(точная) нижняя грань =
наибольшая
(точная) нижняя грань =
 .
.
6. Равномощные множества. Счетные множества, их свойства. Пример бесконечного несчетного множества.
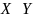 равномощные множества
равномощные множества
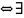 биекция
биекция
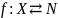 ,
где
,
где
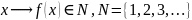 .
.
Свойства:
 бесконечное
множество
бесконечное
множество
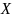 содержит счетное подмножество.
содержит счетное подмножество.
Доказательство:
– бесконечное,
,
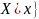 – бесконечное.
– бесконечное.
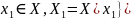 .
.
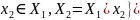 .
.
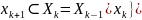 .
.
 -
счетное
подмножество в
-
счетное
подмножество в
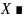 .
.
– счётно,
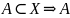 конечно или счётно.
конечно или счётно.
Доказательство:
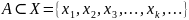 .
.
 первый
первый
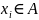 ;
;
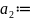 второй
.
второй
.
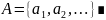
– счётно,
 – конечно или счётно
– конечно или счётно
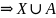 счётно.
счётно.
Доказательство:

– бесконечно, – конечно или счётно
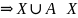 .
.
Доказательство:
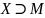 счётное.
счётное.
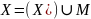 .
.
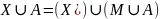 ,
где
,
где
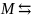 (биекция по свойству 3))
(биекция по свойству 3))
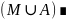 .
.
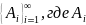 – конечно
или счётно
– конечно
или счётно
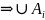 – счётно.
– счётно.
Доказательство аналогично 3).
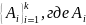 – счётно
– счётно
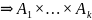 – счётно.
– счётно.
Доказательство:
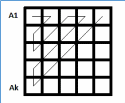 ■
■
Пример:
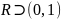 – бесконечное несчётное.
– бесконечное несчётное.
 .
.
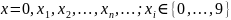
Докажем,
что
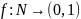 не сюръекция, т.е.
не сюръекция, т.е.
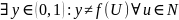 .
.
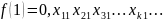 ;
;
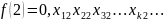 ;
;
 .
Новый
.
Новый
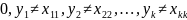 – у него нет номера.
– у него нет номера.