Шейкерне сортування.

Обидва алгоритми згідно із визначаючим принципом вимагають досить великої кількості обмінів. Тому виникає питання, чи не вдасться підвищити їх ефективність хоча б за рахунок зменшення операцій порівняння? Цього можна добитися при допомозі наступних покращень :

1) фіксувати, чи були перестановки в процесі деякого етапу. Якщо ні, то - кінець алгоритму;

2) фіксувати крім факту обміну ще і положення (індекс) останнього обміну. Очевидно, що всі елементи перед ним або після нього відповідно для сортування “бульбашкою” або “камінцем” будуть впорядковані ;

3) почергово використовувати алгоритми “бульбашки” і “камінця”. Тому що для чистої “бульбашки” за один прохід “легкий” елемент виштовхується на своє місце, а “важкий” опускається лише на один рівень. Аналогічна ситуація з точністю до навпаки і для “камінця”. Такий алгоритм називається “шейкерним” сортуванням.

5. Швидкі алгоритми сортування масивів. Алгоритм Шелла, Quick Sort, Heap Sort. Сортування включенням із зменшуваними відстаннями - алгоритм Шелла (1959).

Шелл вдосконалив пряме включення. Він запропонував проводити послідовне впорядкування підмасивів з елементів, які знаходяться на великих відстанях. При цьому на кожному наступному етапі відстані між елементами в групах мають зменшуватися.

Для ілюстрації алгоритму розглянемо його покрокове описання. Не обмежуючи загальності, в якості прикладу спочатку зупинимося на масиві з кількістю елементів, що є степенем двійки, тобто :

1. на першому етапі окремо групуються і сортуються елементи, розміщені на відстані 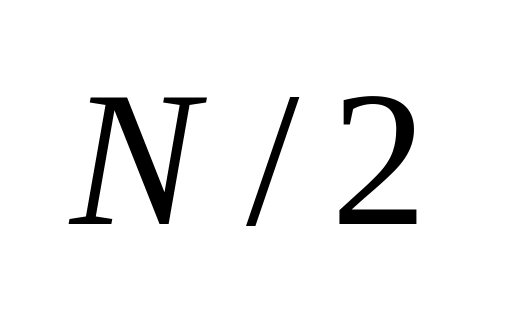. Це є впорядкування підмасивів по 2 елементи, яке називатимемо N/2-сортування.

2. на другому етапі виконується впорядкування підмасивів по 4 елементи на відстані - -сортування і т.д.

На останньому етапі виконується одинарне сортування (впорядкування на відстані

Наприклад :

Кількість етапів сортування t як і відстані на кожному з них можна вибирати довільно. Зокрема, це може буди кількість цілочисельних поділів числа N на 2. тобто t=[log(N)].

Сортування обміном на великих відстанях - алгоритм Quick Sort.

Природно попробувати пришвидшити процес сортування сусідніх пар, порівнюючи пари елементів, що знаходяться далеко один від одного в масиві. К. Хоор розробив алгоритм Quick Sort із середнім часом роботи порядку .

Припустимо, що перший елемент масиву, що сортується, є хорошим наближенням елемента, який вкінці опиниться на своєму місці у відсортованій послідовності. Приймемо його значення в якості ведучого елемента, відносно якого ключі будуть мінятися місцями. Для зручності реалізації алгоритму використаємо два вказівники І, J, перший з яких вестиме відлік вздовж розглядуваної частини масиву зліва, а друтий - справа. Початково їх значення будуть відповідно 1=1, J=N.

Таким чином ведучим елементом буде значення а[І]. Перестановки ключів проводяться за такими принципами:

1) порівнюються елементи а[І] та a[J]; якщо , то здійснюється крок вліво J:=J-1; і порівняння повторюється; зменшення J продовжується доти, поки не виконається умова а[І]> a[J];

2. якщо при порівнянні елементів досягнута умова а[І]> a[J], то проводиться обмін місцями ключів а[І] та a[J] і здійснюється крок вправо І:=І+1; таким чином ведучий елемент перейшов в позицію J; порівняння ключів із збільшенням І продовжується доти, поки знову не виконається умова а[І]> a[J];

3. у випадку виконання умови а[І]> a[J] проводиться обмін місцями ключів а[І] та a[J] і здійснюється крок вліво J:=J-1; при цьому ведучий елемент знову повертається в позицію І.

Цей процес із почерговим зменшенням J та збільшенням І повторюється з обох кінців послідовності до "середини" до тих пір, поки не досягнеться I=J.

Тепер мають місце два факти. По-перше, ключ, що був першим у вихідній послідовності, в результаті такого впорядкування опиняється на "своєму" місці. По-друге, всі елементи зліва будуть меншими за нього, а всі ключі справа - більшими.

Ту ж саму процедуру можна використати для впорядкування лівої і правої підпослідовностей і т. д. до повного сортування всього масиву. Найкращий результат матиме місце, коли на кожному етапі ведучий елемент опинятиметься приблизно посередині сортованої частини масиву.