Задание 1.
Рассматриваем вариационный ряд, соответствующий Вашему варианту.
Найти:
Составить интервальный ряд распределения.
Построить гистограмму частот, кумуляту.
Найти и построить эмпирическую функцию распределения.
Вычислить выборочную среднюю, выборочную и исправленную выборочную дисперсии, выборочное и исправленное СКО, моду, медиану, асимметрию, эксцесс.
Порядок выполнения работы.
Составьте исходную таблицу рассматриваемого признака.
Найдите размах варьирования.
Рассчитайте длину интервала по формуле . Число промежутков гистограммы равно , где . За значение левого конца первого промежутка принимают , за значение правого конца . Все остальные значения концов промежутков получаются по формуле , .
Составьте статистическое распределение частот интервального вариационного ряда признака X.
Вычислите частоту значений , относительную частоту значения : накопленную частоту , накопленную относительную частоту . Заполните следующую таблицу:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Построить прямоугольники, основаниями которых служат частичные интервалы длиной , а высоты равны отношениям
.
Получим гистограмму относительных
частот.Найдите и постройте эмпирическую функцию распределения признака . Результаты вычислений представим в виде таблицы:
В системе координат
построить ломаную, соединяющую точки
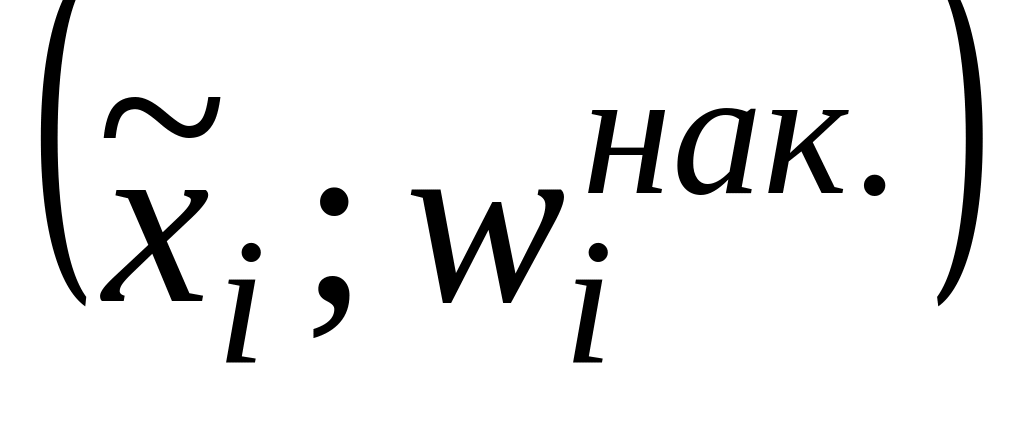.Найдите точечные оценки параметров распределения признака (выборочная средняя, выборочная и исправленная выборочная дисперсия, выборочное и исправленное СКО, мода, медиана, асимметрия, эксцесс).