2.4.3. Расчет основных метрологических характеристик результатов прямых равноточных измерений (Булатов м.И., 1986)

2.4.3.1. Оценка воспроизводимости результатов измерений

Среднее выборки. Пусть x₁, х₂, ..., х_п обозначают п результатов измерений величины, истинное значение которой . Предполагается, что все измерения проделаны одним методом и с одинаковой тщательностью.

В теории ошибок доказывается, что при условии выполнения нормального закона (закона распределения Гаусса) при п измерениях одинаковой точности среднее арифметическое из результатов, полученных при всех измерениях, является наиболее вероятным и наилучшим значением измеряемой величины:

Это среднее значение принимают за приближенное и пишут

Единичное отклонение – отклонение отдельного измерения от среднего арифметического:

Алгебраическая сумма единичных отклонений равна нулю:

Дисперсия, стандартное отклонение и относительное стандартное отклонение. Рассеяние результатов измерений относительно среднего значения принято характеризовать дисперсией s²

или

стандартным отклонением (средним квадратическим отклонением – СКО) – s,

,

которое обычно приводят при представлении результатов измерений и которым характеризуют их воспроизводимость. Стандартное отклонение, деленное на среднее выборки, называют относительным стандартным отклонением

.

В общем случае метод анализа оптимален в той области содержаний, в которой и абсолютное (s), и относительное (s_r) стандартное отклонения имеют минимальные значения.

Дисперсия среднего арифметического, стандартное отклонение среднего арифметического. При оценке воспроизводимости полученных результатов вычисляют также дисперсию среднего арифметического

и стандартное отклонение среднего арифметического (СКО среднего арифметического):

2.4.3.2. Оценка правильности результатов измерений

Доверительный интервал ( ). Если воспроизводимость результатов измерений характеризуют стандартным отклонением, то сами результаты измерений характеризуют доверительным интервалом среднего значения , который рассчитывают по формуле:

где t_Р,f – коэффициент распределения Стьюдента при числе степеней свободы f = п – 1 и двусторонней доверительной вероятности Р. Обычно для расчетов доверительного интервала пользуются значением Р = 0,95.

2.4.4. Расчет уравнения градуировочного графика, его метрологических

характеристик и метрологических характеристик результатов

анализа

2.4.4.1. Вычисление метрологических характеристик линейного графика

Вычисление параметров а и b. В общем случае линейная зависимость выражается уравнением:

.

Значения параметров а и b вычисляют методом регрессионного анализа. Если имеется п взаимосвязанных пар значений (x_i, y_i), то можно записать:

где п – число измерений, х_i – известное содержание (концентрация) определяемого компонента в i-м стандартном растворе; y_i – результат прямых измерений аналитического сигнала i-гo стандартного раствора.

В левой части системы уравнений находятся измеренные значения у_i, а в правой – вычисленные значения Y_i = а + bх_i. Разность между обеими величинами дает погрешность. Аналитически задача метода наименьших квадратов может быть выражена в следующей форме:

.

Если тогда

, i = 1, . . . ., n (2)

Для того чтобы найти параметры а и b, удовлетворяющие минимуму S, берут частные производные выражения (2) относительно а, затем относительно b, полученные выражения приравнивают нулю и, решая уравнения, находят:

или

где и .

или .

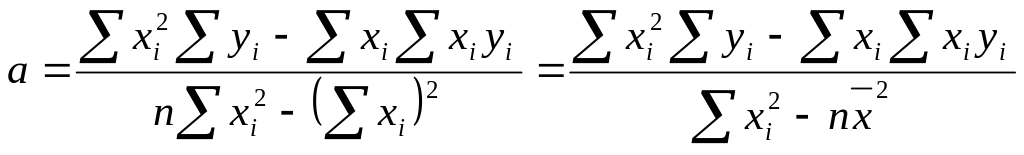Константы а и b являются случайными величинами, поэтому необходима оценка их доверительных интервалов.

Дисперсии констант а и b. Дисперсии констант а и b вычисляют по уравнениям

,

со степенями свободы f = п – 2.

Дисперсию s_yx, характеризующую рассеяние результатов относительно прямой, вычисляют по формуле

со степенями свободы f = п – 2.

Сумму квадратов в уравнении определяют, пользуясь следующим выражением:

.

Доверительный интервал для значений констант а и b. Доверительный интервал для а и b рассчитывают по уравнениям:

при f = п – 2 или. Зная b и а, определяют число необходимых знаков после запятой для b и а.

Доверительный интервал вычисляемых значений зависимой переменной Y_k. Полученную функцию у = a + bx используют для расчета Y_k и Y_k для одного заданного значения x_k. Доверительный интервал для вычисленного значения Y_k рассчитывают по формуле:

.
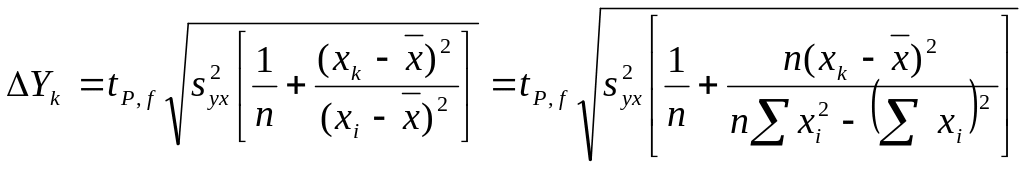