15. Дисперсионный анализ. Межгрупповая вариация. Внутри групповая вариация. Однофакторный дисперсионный анализ.

Дисперсионный анализ — это статистический метод оценки связи между факторными и результативным признаками в различных группах, отобранный случайным образом, основанный на определении различий (разнообразия) значений признаков. В основе дисперсионного анализа лежит анализ отклонений всех единиц исследуемой совокупности от среднего арифметического. В качестве меры отклонений берется дисперсия (В)— средний квадрат отклонений. Отклонения, вызываемые воздействием факторного признака (фактора) сравниваются с величиной отклонений, вызываемых случайными обстоятельствами. Если отклонения, вызываемые факторным признаком, более существенны, чем случайные отклонения, то считается, что фактор оказывает существенное влияние на результативный признак.

Факторная (межгрупповая) дисперсия характеризуется различием средних в каждой группе и зависит от влияния исследуемого фактора, по которому дифференцируется каждая группа. Например, в группах различных по этиологическому фактору клинического течения пневмонии средний уровень проведенного койко-дня неодинаков — наблюдается межгрупповое разнообразие.

Остаточная (внутригрупповая) дисперсия характеризует рассеяние вариант внутри групп. Отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неуточненных факторов и не зависящую от признака — фактора, положенного в основание группировки. Вариация изучаемого признака зависит от силы влияния каких-то неучтенных случайных факторов, как от организованных (заданных исследователем), так и от случайных (неизвестных) факторов.

Дисперсионный анализ, в котором проверяется влияние одного фактора, называется однофакторным (одномерный анализ). При изучении влияния более чем одного фактора используют многофакторный дисперсионный анализ (многомерный анализ).

Факторные признаки — это те признаки, которые влияют на изучаемое явление.

Результативные признаки — это те признаки, которые изменяются под влиянием факторных признаков.

Условия применения дисперсионного анализа:

Задачей исследования является определение силы влияния одного (до 3) факторов на результат или определение силы совместного влияния различных факторов (пол и возраст, физическая активность и питание и т.д.).

Изучаемые факторы должны быть независимые (несвязанные) между собой. Например, нельзя изучать совместное влияние стажа работы и возраста, роста и веса детей и т.д. на заболеваемость населения.

Подбор групп для исследования проводится рандомизированно (случайный отбор). Организация дисперсионного комплекса с выполнением принципа случайности отбора вариантов называется рандомизацией (перев. с англ. — random), т.е. выбранные наугад.

Можно применять как количественные, так и качественные (атрибутивные) признаки.

16. Временные ряды. Элементы временного ряда (тренд, сезонная вариация, ошибки mad и mse).

Временным рядом (рядом динамики, динамическим рядом) называется последовательность значений показателя (признака), упорядоченная в хронологическом порядке, т.е. в порядке возрастания временного параметра. Отдельные наблюдения временного ряда называются уровнями этого ряда.

Каждый временной ряд содержит два элемента:

1) значения времени;

2) соответствующие им значения уровней ряда.

В качестве показателя времени в рядах динамики могут указываться либо определенные моменты времени (даты), либо отдельные периоды (сутки, месяцы, кварталы, полугодия, годы и т.д.). В зависимости от характера временного параметра ряды делятся на моментные и интервальные.

Одним из важнейших условий, необходимых для правильного отражения временным рядом реального процесса развития, является сопоставимость уровней ряда. Для несопоставимых величин неправомерно проводить исследование динамики.

Под трендом понимают изменение, определяющее общее направление развития, основную тенденцию временного ряда. Это систематическая составляющая долговременного действия.

Если период колебаний не превышает одного года, то их называют сезонными. Чаще всего причиной их возникновения считаются природно-климатические условия..

При большем периоде колебания считают, что во временных рядах имеет место циклическая составляющая. Примерами могут служить демографические, инвестиционные и другие циклы.

Если из временного ряда удалить тренд и периодические составляющие, то останется нерегулярная компонента.

Экономисты разделяют факторы, под действием которых формируется нерегулярная компонента, на 2 вида:

• факторы резкого, внезапного действия;

• текущие факторы.

Факторы первого вида (например, стихийные бедствия, эпидемии и др.), как правило, вызывают более значительные отклонения. Иногда такие отклонения называют катастрофическими колебаниями.

Факторы второго вида вызывают случайные колебания, являющиеся результатом действия большого числа побочных причин. Влияние каждого из текущих факторов незначительно, но ощущается их суммарное воздействие.

В большинстве случаев значения переменных характеризуют не только тренд. Часто они подвержены циклическим колебаниям. Если эти колебания повторяются в течение небольшого промежутка времени, то они называются сезонной вариацией. Колебания, повторяющиеся в течение более длительного промежутка времени, называются циклической вариацией.

Среднее абсолютное отклонение (mean absolute deviation - MAD):

равное отношению суммы величин всех ошибок без учета их знака к общему числу наблюдений.

Среднеквадратическая ошибка (mean square error - MCE):

которая представляет собой отношение суммы квадратов ошибок к общему числу наблюдений.

17. Расчет сезонной вариации в аддитивной модели. Центрированная скользящая средняя.

Моделью с аддитивной компонентой называется такая модель, в которой вариация значений переменной во времени наилучшим образом описывается через сложение отдельных компонент.

Аддитивную модель: Х=Т+S+Е применяют в случае, когда амплитуда сезонных колебаний со временем не меняется.

 Сезонная вариация — краткосрочно регулярно повторяющееся колебания значений временного ряда вокруг тренда;

Введем обозначения.

Пусть имеется временной ряд – Х_ij,

 где i – номер сезона (периода времени внутри года, например месяца, квартала); i=1;L (L – число сезонов в году);

j – номер года, j=1;m (m – всего лет).

Тогда количество исходных уровней ряда равно L m=n.

В качестве сезонной компоненты для аддитивной модели применяют абсолютное отклонение – Sa_i, Сезонные компоненты должны отвечать определенным требованиям:

           в случае аддитивной модели сумма всех сезонных компонент должна быть равна нулю;

           в случае мультипликативной модели произведение всех сезонных компонент должно быть равно единице.

Перед расчетом сезонных компонент ряд динамики выравнивают. Чаще всего используют алгоритмическое (механическое) выравнивание (например, метод скользящей средней). В результате получают выровненный ряд:  , который не содержит сезонной компоненты.

Абсолютное отклонение в 1-ом сезоне определяется как среднее арифметическое из отклонений фактического и выровненного уровней ряда:

.

Индекс сезонности в i-м сезоне определяется как среднее арифметическое из отношений фактического уровня ряда к выровненному:

Скользящая средняя – это переменная значения которой равны среднему арифметическому значения исследуемой величины в точке для которой она вычисляется и значений всех точек, отстоящих от нее на 0.5*(L - 1) слева и справа в случае если L нечетное и 0.5L – если L четное. При вычислении значения скользящей средней для следующей точки временного ряда номера точек, участвующих в вычислении смещаются на единицу. 

Суть метода скользящей средней заключается в замене фактических данных расчетными - средними арифметическими из нескольких уровней временного ряда.

Так как временной ряд имеет периодические сезонные колебания с жесткой продолжительностью цикла (4 квартала), то их можно полностью устранить с помощью скользящей средней, если взять интервал сглаживания m = 4.

Первый член сглаженного ряда по 4-х членной скользящей средней рассчитывается по формуле:

Для определения 2-го сглаженного уровня подсчет сумм 4-х членов ряда начинается со 2-го члена и заканчивается 5-м, т. е. по формуле:

Для определения t-ro сглаженного уровня используется формула:

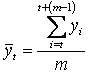
где m - число уровней в интервале сглаживания, m = 4: t - порядковый номер сглаженного уровня.

С целью получения средних, соответствующих тем же интервалам времени, что и фактические данные, производят операцию центрирования. Центрированные скользящие средние находят по формулам двучленной скользящей средней:

Полученное таким образом множество значений центрированных скользящих средних представляет наилучшую оценку тренда.

18. Расчет уравнения тренда в аддитивной модели.

Оцененное уравнение линейного тренда имеет вид:

где t - порядковый номер квартала: ао. ai - неизвестные параметры.

Параметры уравнения тренда оцениваются методом наименьших квадратов по формулам:

19. Расчет ошибок в аддитивной модели.

20. Прогнозирование в аддитивной модели.

21. Расчет сезонной вариации в мультипликативной модели. Центрированная скользящая средняя.

22. Прогнозирование в мультипликативной модели.

23. Экспоненциальное сглаживание. Простая модель экспоненциального сглаживания. Константа сглаживания.

24. Выборочные уравнения регрессии. Линейная корреляция. Корреляционная таблица. Выборочное уравнение прямой линии регрессии У на X.

25. Выбор метода прогнозирования.

При выборе метода прогнозирования надо учитывать два момента:

1. Нужно обеспечить полноту, точность и достоверность прогноза.

2. Необходимо снизить затраты на разработку прогноза.

Критериями выбора являются:

1. Особенности объекта прогнозирования.

2. Цели прогнозирования.

3. Срок упреждения.

4. Уровень управления, для которого разрабатывают прогноз.

Четыре класса задач прогнозирования:

1. Стандартные задачи – в этом случае изменение фактора приводит к однозначному результату. Зависимость между фактом и результатом можно выразить математической формулой.

2. Структурированные задачи – при изменении фактора результат определяется однозначно или может меняться в узком интервале значений.

3. Слабоструктурированные задачи – изменение фактора приводит к изменению результата в достаточно широком интервале значений.

4. Неструктурированные задачи – изменение фактора может приводить к непредсказуемому результату.

Класс проблем зависит от особенностей объекта прогнозирования, уровня управления и срока упреждения.

Чем выше уровень управления, тем ниже уровень структурированности задачи прогнозирования. Чем выше интервал прогнозирования, тем ниже уровень структурированности задачи прогнозирования.

Для стандартных задач применяют методы экстраполяции и трендовые модели. Для структурированных – трендовые и экономические. Для слабоструктурированных – эконометрические модели и методы экспертных оценок. Для неструктурированных – методы экспертных оценок.

26. Адаптивные методы прогнозирования в экономических исследованиях

Адаптивные методы позволяют учесть различную информационную ценность уровней временного ряда, степень «устаревания» данных. Адаптивными называются методы прогнозирования, позволяющие строить самокорректирующиеся (самонастраивающиеся) экономико-математические модели, которые способны оперативно реагировать на изменение условий путем учета результата прогноза, сделанного на предыдущем шаге, и учета различной информационной ценности уровней ряда.

Благодаря указанным свойствам адаптивные методы особенно удачно используются при краткосрочном прогнозировании (при прогнозировании на один или на несколько шагов вперед).

Указанное определение отражает основные характерные черты, присущие рассматриваемому подходу. В то же время деление на адаптивные и неадаптивные модели часто носит достаточно условный характер.

У истоков адаптивных методов лежит модель экспоненциального сглаживания.

27. Модели экономического прогнозирования

Экономическое моделирование основано на обработке статистической информации ретроспективного характера, оценке отдельных переменных величин, их параметров.

С учетом фактора времени модели могут быть статическими (т.е. когда ограничения в модели установлены для одного определенного отрезка времени в течение планового периода и при этом минимизируются затраты или максимизируется конечный результат), или динамическими (в этом случае ограничения установлены для нескольких отрезков времени при той же минимизации или максимизации эффекта за весь плановый период).

Принято различать следующие эконометрические модели: факторные, структурные и комбинированные. Один и тот же тип моделей может быть применим к различным экономическим объектам.

В зависимости от уровня агрегирования показателей развития народного хозяйства различают макроэкономические, межотраслевые, региональные микроэкономические модели.

По аспектам развития экономики различают модели воспроизводства основных фондов, трудовых ресурсов, системы финансов и ценообразования.

Факторные модели описывают зависимость уровня и динамики того или иного экономического показателя от уровня и динамики влияющих на него экономических показателей-аргументов.

Переменные эконометрической модели подразделяются на экзогенные (внешние) и эндогенные (внутренние). Например, экзогенный фактор в модели может представлять собой для предприятия ритмичность поставок; эндогенный - наличие трудовых ресурсов на предприятии.

Факторные модели могут включать различное количество переменных величин и соответствующих им параметров. Простейшими видами факторных моделей являются однофакторные, в которых фактором является какой-либо временной параметр. В этом случае анализ и прогноз какого-либо показателя осуществляется в зависимости от хронологического ряда времени, и тем самым выявляются тренды (зависимости, характеризующие общую тенденцию изменения какого-либо динамического ряда).

Многофакторные модели линейного, нелинейного типа позволяют одновременно учитывать воздействие нескольких факторов на уровень и динамику прогнозируемого показателя. Такими моделями могут быть модели, описывающие макроэкономические производственные функции, модели анализа спроса на отдельные предметы потребления в зависимости от доходов населения, цен, уровня насыщения, рациональных норм потребления и др.

Структурные модели описывают соотношения, связи между отдельными элементами, образующими одно целое или агрегат. Эти модели являются моделями структурно-балансового типа, где наряду с разбивкой какого-либо агрегата на составляющие элементы рассматриваются взаимосвязи этих элементов. Такие модели имеют матричную форму и применяются для анализа и прогноза межотраслевых и межрайонных связей. С их помощью описываются взаимосвязи потоков. В зависимости от номенклатуры продукции, сырья и других факторов различают однопродуктовые и многопродуктовые модели. К первым относятся модели, в которых установлено одно ограничение по спросу на продукцию, вырабатываемую отраслью в целом, либо одно ограничение на количество сырья или другого ресурса, потребляемого ею.

28. Трендовые модели

1. Модели

- постоянный рост:

– линейная;

- увеличивающийся рост:

– парабола,

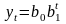– показательная;

- уменьшающийся рост:

- линейная логарифмическая;

при < 1 – степенная;

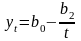- модифицированная гипербола;

– модифицированная экспонента;

- комбинированный рост:

с – логарифмическая парабола;

с - полином третьей степени.

- рост с качественным изменением динамических характеристик:

– кривая Гомпертца;

- логистическая кривая Перла – Рида.

2. Критерий Дарбина-Уотсона

(7.1)

(7.2)

где S_y – среднеквадратическая ошибка модели;

t₁ – время упреждения, для которого делается экстраполяция, t₁ = n + l;

t - порядковый номер уровней ряда, t= 1,2,…, n;

- порядковый номер уровня, стоящего в середине ряда

29. Регрессионные модели

Регрессионная модель — это параметрическое семейство функций, задающее отображение.

1. Оценки коэффициентов однофакторной регрессионной модели

(8.1)

(8.2)

где

, , , (8.3)

где х – независимая переменная,

у - зависимая переменная,

N – число элементов выборочной совокупности.

2. Коэффициент корреляции

, (8.4)

где , – среднеквадратические ошибки, вычисляемые по формулам

(8.5)

(8.6)

3. Коэффициент детерминации

(8.7)

4. Дисперсионное отношение Фишера (F – критерий)

, (8.8)

где – расчетное значение зависимой переменной (например, для случая линейной однофакторной модели ),

n - число элементов выборочной совокупности,

m - число факторов.

5. Стандартные ошибки параметров линейной регрессии

(8.9)

, (8.10)

где – остаточная дисперсия, рассчитываемая по формуле:

(8.11)

6. t-статистики Стьюдента

(8.12)

7. Доверительные интервалы для коэффициентов регрессии

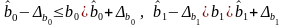(8.13)

где - предельные ошибки, рассчитываемые по формулам

(8.14)

где – табличное значение t-статистики.

8. Индекс корреляции

(8.15)

9. Усредненное значение коэффициента эластичности

(8.16)

10. Доверительные интервалы прогноза

(8.17)

где L – период упреждения, .

11. Оценки вектора коэффициентов регрессии

(8.18)

12. Стандартная ошибка -го коэффициента регрессии, равная корню квадратному из соответствующего диагонального элемента ковариационной матрицы векторной оценки

(8.19)

где рассчитывается по остаткам .

13. Множественный индекс корреляции

(8.20)

14. Бетта - коэффициенты

(8.21)

15. Парные коэффициенты корреляции

(8.22)

16. Множественный коэффициент корреляции

(8.23)

17. Скорректированный коэффициент множественной детерминации

(8.24)

18. Частный F-критерий

(8.25)

19. Стандартная ошибка прогноза среднего

(8.26)

20. Для проверки гипотезы о равенстве прогноза среднего значения заданной величине рассчитывается - статистика

(8.27)

30. Простые скользящие средние

Распространенным приемом при выявлении и анализе тенденции развития является сглаживание временного ряда. Суть различных приемов сглаживания сводится к замене фактических уровней временного ряда расчетными уровнями, которые в меньшей степени подвержены колебаниям. Это способствует более четкому проявлению тенденции развития.

Методы сглаживания можно условно разделить на два класса, опирающиеся на различные подходы:

• аналитический подход;

• алгоритмический подход.

Аналитический подход основан на допущении, что исследователь может задать общий вид функции, описывающей регулярную, неслучайную составляющую. Например, на основе визуального и содержательного экономического анализа динамики временного ряда предполагается, что трендовая составляющая может быть описана с помощью показательной функции:

Тогда на следующем этапе будет произведена статистическая оценка неизвестных коэффициентов модели, а затем определены сглаженные значения уровней временного ряда путем подстановки соответствующего значения временного параметра t в полученное уравнение (заданное в явном аналитическом виде). Процедуры моделирования, опирающиеся на этот подход, рассматриваются в следующей главе.

При использовании алгоритмического подхода отказываются от ограничительного допущения, свойственного аналитическому. Процедуры этого класса не предполагают описания динамики неслучайной составляющей с помощью единой функции, они предоставляют исследователю лишь алгоритм расчета неслучайной составляющей в любой заданный момент времени t. Методы сглаживания временных рядов с помощью скользящих средних относятся к этому подходу. ]

Иногда скользящие средние применяют как предварительный этап перед моделированием тренда с помощью процедур, относящихся к аналитическому подходу.

Скользящие средние позволяют сгладить как случайные, так и периодические колебания, выявить имеющуюся тенденцию в развитии процесса, и поэтому служат важным инструментом при фильтрации компонент временного ряда.

Алгоритм сглаживания по простой скользящей средней может быть представлен в виде следующей последовательности шагов:

1. Определяют длину интервала сглаживания l, включающего в себя l последовательных уровней ряда (l < n). При этом надо иметь в виду, что чем шире интервал сглаживания, тем в большей степени взаимопогашаются колебания, и тенденция развития носит более плавный, сглаженный характер. Чем сильнее колебания, тем шире должен быть интервал сглаживания.

2. Разбивают весь период наблюдения на участки, при этом интервал сглаживания как бы скользит по ряду с шагом, равным 1.

3. Рассчитывают средние арифметические из уровней ряда, образующих каждый участок.

4. Заменяют фактические значения ряда, стоящие в центре каждого участка, на соответствующие средние значения.

При этом удобно брать длину интервала сглаживания l в виде нечетного числа: l = 2p + 1, т.к. в этом случае полученные значения скользящей средней приходятся на средний член интервала.

Наблюдения, которые берутся для расчета среднего значения, называются активным участком сглаживания.

При нечетном значении l все уровни активного участка могут быть представлены в виде:

, (2.1)

где: - центральный уровень активного участка;

- последовательность из p уровней активного участка, предшествующих центральному;

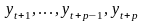- последовательность из p уровней активного участка, следующих за центральным.

Тогда скользящая средняя рассчитывается по формуле:

. (2.2)

где: - фактическое значение i–го уровня;

- значение скользящей средней в момент t;

- длина интервала сглаживания.

Процедура сглаживания приводит к устранению периодических колебаний во временном ряду, если длина интервала сглаживания берется равной или кратной периоду колебаний.

Для устранения сезонных колебаний часто требуется использовать четырех- и двенадцатичленные скользящие средние, но при этом не будет выполняться условие нечетности длины интервала сглаживания. Поэтому при четном числе уровней принято первое и последнее наблюдение на активном участке брать с половинными весами:

(2.3)

Тогда для сглаживания сезонных колебаний при работе с временными рядами квартальной или месячной динамики можно использовать 4-членные (2.3) и 12-членные (2.4) скользящие средние:

, (2.4)

. (2.5)

В (2.3) каждый активный участок содержит 5 уровней, в (2.4) —13, при этом крайние уровни имеют половинные весовые коэффициенты.

При использовании скользящей средней с длиной активного участка l = 2p + 1 первые и последние p уровней ряда сгладить нельзя, их значения теряются. Очевидно, что потеря значений последних точек является существенным недостатком, так как для исследователя последние «свежие» данные обладают наибольшей информационной ценностью.

Рассмотрим один из приемов, позволяющих восстановить потерянные значения временного ряда при использовании простой скользящей средней. Для этого необходимо:

1) Вычислить средний абсолютный прирост на последнем активном участке

, (2.6)

, (2.7)

где - длина активного участка;

- значение последнего уровня на активном участке;

- значение первого уровня на активном участке;

- средний абсолютный прирост на последнем активном участке.

2) Получить p сглаженных значений в конце временного ряда путем последовательного прибавления среднего абсолютного прироста к последнему сглаженному значению.

Аналогичную процедуру можно реализовать для оценивания первых уровней временного ряда.

Метод простой скользящей средней применим, если графическое изображение динамического ряда напоминает прямую. Когда тренд выравниваемого ряда имеет изгибы и для исследователя желательно сохранить мелкие волны, то применение простой скользящей средней нецелесообразно.

Если для процесса характерно нелинейное развитие, то простая скользящая средняя может привести к существенным искажениям. В этих случаях следует обратиться к взвешенной скользящей средней.

31. Взвешенные скользящие средние

Взвешенное скользящее среднее - скользящее среднее, при вычислении которого вес каждого члена исходной функции, начиная с меньшего, равен соответствующему члену арифметической прогрессии.

P – это цена актива в определенном периоде, значение W – удельный вес. Взвешенные скользящие средние - это средние, которые придают больший вес новым данным и меньший - старым. Взвешенная скользящая средняя вычисляется умножением данных каждого предыдущего дня на определенный вес. Чтобы рассчитать этот вид скользящей средней, мы должны придать вес 1 самым старым данным, затем 2 - следующим данным и так далее, до текущей цены. Применяемый вес основан на сумме числа дней в скользящей средней. Для расчета 5-дневной WMA вес первого дня вычисляют так: Дата Цена актива

1 мая 102

2 мая 105

3 мая 107

4 мая 106

5 мая 109

32. Модели кривых роста в экономическом прогнозировании

Под кривой роста понимают функцию, аппроксимирующую заданный динамический ряд. Разработка прогноза с использованием кривых роста включает следующие этапы:

1. выбор одной или нескольких кривых, форма которых соответствует динамике временного ряда; 2. оценка параметров выбранных кривых; 3. проверка адекватности выбранных кривых прогнозируемому процессу и окончательный выбор кривой; 4. расчет точечного и интервального прогнозов.

Кривые роста обычно выбираются из трех классов функций. К первому классу относятся кривые, которые используются для описания процессов с монотонным характером развития и отсутствием пределов роста. Ко второму классу относятся кривые, имеющие предел роста в иссле­дуемом периоде. Такие кривые называют кривыми насыщения. Если кривые насыщения имеют точки перегиба, то они относятся к кривым третьего класса. Их называют S - образными кривыми. Среди кривых роста первого типа выделяют класс полиномов:

уt = а0 + а1t + а2t2 + а3t3 + ... Параметр а0 является начальным уровнем рядапри t = 0, а1 - линейный прирост, а2 — ускорение роста, а3 — изменение ускорения роста. В эконометрических исследованиях в большинстве случаях применяются полиномы не выше третьего порядка.

33. Методы выбора кривых роста

Наиболее простой метод – визуальный, опирающийся на графическое изображение временных рядов. Подбирают такую кривую роста, форма которой соответствует фактическому развитию процесса. Если тенденция на графике просматривается недостаточно четко, то проводят преобразование исходного ряда. В литературе описан также метод последовательных разностей (помогает в выборе кривых параболического типа).

Этот метод применяют при выполнении следующих предположений:

1) уровни ряда могут быть представлены в виде суммы трендовой составляющей и случайной компоненты, подчиненной закону нормального распределения с математическим ожиданием, равным нулю и постоянной дисперсией; метод последующих разностей предполагает вычисление первых, вторых и т.д. разностей уровней ряда:

Расчет ведется до тех пор, пока разности не будут примерно равными. Порядок разностей принимается за степень выравнивающего полинома.

В отдельных случаях используют метод характеристик прироста. Процедура выбора кривых роста с использованием этого метода включает:

1) выравнивание ряда по скользящей средней;

2) определение средних приростов;

3) вычисление производных характеристик прироста

34. Доверительные интервалы прогноза, проверка адекватности выбранных моделей

Прогнозные значения исследуемого показателя вычисляют путем подстановки в уравнение кривой значений времени t, соответствующих периоду упреждения. Полученный таким образом прогноз называется точечным прогнозом. На практике в дополнение к точечному определяют границы возможного значения прогнозированного показателя, то есть вычисляют интервальный прогноз.

Доверительный интервал прогноза определяется в следующем виде:

 

Ширина доверительного интервала зависит от уровня значимости, периода упреждения, среднего квадратического отклонения от тренда и степени полинома. Чем выше степень полинома, тем шире доверительный интервал при одном и том же значении Sр, так как дисперсия уравнения тренда вычисляется как взвешенная сумма дисперсий соответствующих параметров уравнения. Доверительные интервалы прогнозов, полученных с использованием уравнения экспоненты, определяют аналогичным образом.

Проверка адекватности выбранных моделей реальному процессу строится на анализе случайной компоненты. Случайная (остаточная) компонента получается после выделения из исследуемого ряда тренда и периодической составляющей.

35. Модель регрессии: с автокоррелированными остатками

При построении регрессионных моделей чрезвычайно важно соблюдение четвертой предпосылки МНК – отсутствие автокорреляции остатков, т. е. значения остатков распределены независимо друг от друга. Автокорреляция остатков означает наличие корреляции между остатками текущих предыдущих(последующих) наблюдений. Коэффициент корреляции между и , где -остатки текущих наблюдений, - остатки предыдущих наблюдений (например, j= i -1), может быть определен как

,

Т.е. по обычной формуле линейного коэффициента корреляции. Если этот коэффициент окажется существенно отличным от нуля, то остатки автокоррелированы и функция плотности вероятности F(ε) зависит от j-й точки наблюдения и от распределения значений остатков в других точках наблюдения.

Наиболее желательным решением при наличии автокорреляции является попытка выявить ответственный за нее фактор и ввести его в уравнение регрессии. Как правило автокорреляция встречается, когда переменные изменяются со временем, и введение фактора времени в уравнение регрессии в этих случаях решает проблему.

В экономике отрицательная автокорреляция может появляться при преобразовании первоначальной спецификации модели в форму, подходящую для регрессионного анализа.

Отсутствие автокорреляции остаточных величин обеспечивает состоятельность и эффективность оценок коэффициентов регрессии. Особенно актуально соблюдение данной предпосылки МНК при построении регрессионных моделей по рядам динамики, где ввиду наличия тенденции последующие уровни динамического ряда, зависят от своих предыдущих уровней. О специфике исследования остаточных величин по регрессионным моделям по временным рядам.

36. Авторегрессионные модели

Авторегрессия – модель временных рядов, в которой значение временного ряда в данный момент времени может быть выражено в виде линейной комбинации предыдущих значений этого же ряда и случайной ошибки, обладающей свойством «белого шума».

Модель – марковский случайный процесс – случайный процесс, протекающий в системе, если вероятность любого состояния системы в будущем зависит только от её состояния в настоящий момент и не зависит от её состояний в прошлом:

37. Модель динамической регрессии

38. Многофакторные адаптивные модели

39. Модель прогнозирования стабильности цен

Расчетные формулы

Адаптивная авторегрессионная модель

(13.1)

где - фактическое значение цены в момент времени ;

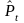- расчетное значение цены в момент времени t;

- вектор коэффициентов авторегрессионной модели;

- значение коэффициента стабильности (авторегрессии) в момент времени t (если , то процесс стабилен, в противном случае – нет);

- вектор текущих значений независимых переменных;

- настраиваемые параметр, регулирующий уровень реакции модели;

-настраиваемый параметр сглаживания.

40. Матричные модели прогнозирования

Расчетные формулы

Модель с детерминированным матричным мультипликатором

(14.1)

где I – единичная матрица;

x_t = - вектор значений показателя в момент времени t;

V= - матрица косвенных темпов роста, внедиагональные элементы которой рассчитываются по формуле

(14.2)

где - матричный мультипликатор.

Модель с настраиваемым параметром матричного мультипликатора

(14.3)

где - матрица темпов роста;

- матрицы косвенных темпов роста, элементы которой рассчитываются по формуле - прямой рост);

- матрицы косвенных темпов роста, элементы которой рассчитываются по формуле ( - косвенный рост); - настраиваемый параметр

Модель с адаптивным матричным мультипликатором

(14.4)

где А_t – начальное значение мультипликатора на момент t, определяемое по формуле

( ) – операция блочного умножения

- корректирующая матрица мультипликатора с элементами ,

- матрица, определяющая соотношение прямых и косвенных темпов роста,

- матрица весовых коэффициентов;

(14.5)

где a^* - параметр адаптации, настраиваемый по критерию минимизации максимальной ошибки

- скорректированное значение матричного мультипликатора.

41. Модели многомерных классификаций в прогнозных расчетах

Определенные виды моделей экономического и социального прогнозирования могут классифицироваться в зависимости от критерия оптимизации или наилучшего ожидаемого результата. Так, например, различают экономико-математические модели, в которых минимизируются затраты, и модели, в которых желательно получить, например, максимум прибыли.

С учетом фактора времени модели могут быть статическими (т.е. когда ограничения в модели установлены для одного определенного отрезка времени в течение планового периода и при этом минимизируются затраты или максимизируется конечный результат), или динамическими (в этом случае ограничения установлены для нескольких отрезков времени при той же минимизации или максимизации эффекта за весь плановый период).

Принято различать следующие эконометрические модели: факторные, структурные и комбинированные. Один и тот же тип моделей может быть применим к различным экономическим объектам.

В зависимости от уровня агрегирования показателей развития народного хозяйства различают макроэкономические, межотраслевые, региональные микроэкономические модели.

По аспектам развития экономики различают модели воспроизводства основных фондов, трудовых ресурсов, системы финансов и ценообразования и др.

Факторные модели описывают зависимость уровня и динамики того или иного экономического показателя от уровня и динамики влияющих на него экономических показателей-аргументов.

Переменные эконометрической модели подразделяются на экзогенные (внешние) и эндогенные (внутренние). Например, экзогенный фактор в модели может представлять собой для предприятия ритмичность поставок; эндогенный - наличие трудовых ресурсов на предприятии.

42. Модель прогнозирования по неполным данным

Хольт развил модель простого экспоненциального сглаживания и добавил в неё тренд.

Метод Хольта используется для прогнозирования временных рядов, когда есть тенденция к росту или падению значений временного ряда. А также для рядов, когда данные есть не за полный цикл, и сезонность еще не выделить (например, за неполный год для прогноза по месяцам).

Если временной ряд имеет тенденцию к росту или падению, то вместе с оценкой текущего уровня ряда (как в простом экспоненциальном сглаживании) стоит выделить тренд. Для управления уровнем и наклоном в модели Хольта вводится 2 коэффициента сглаживания – коэффициент сглаживания ряда и тренда.

1. Рассчитываем экспоненциально-сглаженный ряд:

L_t=k*Y_t+(1-k)*(L_t-1-T_t-1), где

• L_t  – сглаженная величина на текущий период;

• k – коэффициент сглаживания ряда;

• Y_t – текущие значение ряда (например, объём продаж);

• L_t-1 – сглаженная величина за предыдущий период;

• T_t-1 – значение тренда за предыдущий период;

2. Определяем значение тренда

T_t=b*(L_t - L_t-1)+(1-b)*T_t-1,  где:

• T_t – значение тренда на текущий период;

• b – коэффициент сглаживания тренда;

• L_t – экспоненциально сглаженная величина за текущий период;

• L_t-1 – экспоненциально сглаженная величина за предыдущий период;

• T_t-1 – значение тренда за предыдущий период.

3. Делаем прогноз по методу Хольта

Прогноз на p периодов вперед равен:

Ŷt+p = Lt + p *Tt, где

• Ŷt+p – прогноз по методу Хольта на p период;

• Lt – экспоненциально сглаженная величина за последний период;

• p – порядковый номер периода, на который делаем прогноз;

• Tt – тренд за последний период.

43. Модели сезонных колебаний

Расчетные формулы

1. Модель с аддитивной сезонной составляющей

y_t = f(t) + S(t) + ε_t, (17.1)

где f(t) – тренд;

S(t) – сезонная составляющая;

ε_t – случайная компонента.

2. Модель с мультипликативной сезонной составляющей:

y_t = f(t) S(t) ε_t (17.2)

3. Модель временного ряда с циклическими колебаниями периодичностью k:

y_t = b₀ + b₁t + c₁x₁ + c₂x₂ + … + c_k-1x _k-1 + ε_t (17.3)

где xj =

{

1 для j + nk, n = 0, 1, 2, … 0 для всех остальных случаев

44. Критерий настройки параметра адаптации

Как уже неоднократно отмечалось, для проведения расчетов по адаптивным моделям необходимо задать начальные значения   ,   ,   и определить оптимальные в некотором смысле параметры   ,   ,   , а для моделей с многошаговым алгоритмом адаптивного механизма и параметр   .В принципе, для достаточно длинных временных рядов выбор начальных значений может быть произвольным. С течением времени влияние начальных значений на прогнозные расчеты в результате многократного сглаживания перестает ощущаться. Однако в экономике часто приходится иметь дело с короткими временными рядами и, поэтому, от выбора начальных значений зависит точность окончательных результатов. Кроме того, при задании начальных значений мы должны учитывать то обстоятельство, что в самонастраивающейся структуре адаптивного механизма предусмотрен вариант построения адаптивной модели с постоянными коэффициентами, которые по схеме построения такого варианта полагаются равными начальным значениям. Если же выбор начальных значений осуществлять произвольным образом, например, положить все компоненты вектора   равными нулю, то, очевидно, что модель с нулевыми коэффициентами не может представлять по точности предсказания альтернативу модели с переменными коэффициентами. Следовательно, процедура, основанная на произвольном выборе начальных значений, исключает из схемы построения модели важный вариант ее возможной структуры, ухудшая в конечном итоге наследственные свойства адаптивного механизма. Поэтому, в силу приведенных здесь доводов, а также учитывая, что рассматриваемые адаптивные алгоритмы являются рекуррентными вариантами взвешенного МНК, будем для ускорения сходимости к оптимальным оценкам в качестве   задавать матрицу, обратную матрице системы нормальных уравнений обычного МНК  В Вкачестве   и   выбираются векторы коэффициентов регрессионной модели, вычисленные с помощью МНК по данным одних и тех же временных рядов  , (5.69)  , (5.70)где   вектор-столбец оценок коэффициентов регрессионной модели;  вектор-столбец значений зависимой переменной в момент времени   ;  матрица значений независимых переменных из   строк  .Начальные значения, задаваемые в виде (6.68)–(6.70), позволяют в структуре возможных вариантов адаптивной модели предусмотреть регрессионную модель с постоянными коэффициентами, определяемыми по МНК, как альтернативную модели с переменными коэффициентами. Это является убедительным аргументом в пользу такого способа определения начальных значений. Кроме того, известно, что именно этот способ обеспечивает быструю сходимость к оптимальным оценкам МНК.Для определения оптимальных значений   ,   ,   ,   проще всего применить общеизвестный метод перебора. Применение этого метода предполагает наличие критерия, с помощью которого можно из двух наборов   ,   ,   ,   и   ,   ,   ,   различных значений параметров адаптации выбрать наилучший в некотором смысле. В принципе, критерий настройки не обязательно должен быть идентичным по своей структуре функционалу экстремальной задачи. Учитывая это замечание, критерии можно строить таким образом, чтобы они ориентировали настройку параметров адаптации на повышение определенных характеристик точности прогнозных расчетов. Рассмотрим три возможных варианта:

 

 где     .

Первый критерий представляет собой сумму модулей ошибок прогнозирования и используется в тех случаях, когда за счет настраиваемых параметров необходимо получить минимально допустимую в рамках данной модели сумму прогнозных ошибок по всей обучающей последовательности наблюдений. Второй критерий – это сумма модулей максимальных ошибок прогнозирования. Причем, максимальная ошибка выбирается среди ошибок прогнозирования, рассчитанных для скользящего интервала длиной   . Третий критерий аналогичен второму, но только в нем суммируются относительные максимальные ошибки прогнозирования. Применение двух последних критериев следует рекомендовать в тех случаях, когда   и требуется, чтобы уровень ошибки предсказания построенной модели был по возможности равномерно минимальным для всего периода упреждения.Для всех трех критериев в качестве обучающей последовательности используются первые   наблюдений, а в качестве контрольной – группа из   последних наблюдений. Возможны и другие способы формирования обучающей и контрольной последовательности, например, деление всего выборочного множества наблюдений на две равных части – обучающую и контрольную. Настройка параметров адаптивного механизма заключается в определении оптимального набора значений   путем решения экстремальной задачи  , (5.74)в которой в качестве целевого функционала используется любой из выше- приведенных критериев. В  представляет собой прямое произведение множеств  , где   (   – достаточно малая положительная величина),  ,  .Для решения этой задачи методом прямого перебора на множестве значений   строится сетка

 , (5.76)  , (5.77)  , (5.78)  , (5.79)

Для каждого узла   сетки (5.76)–(5.79) по рекуррентным формулам настраиваемого адаптивного алгоритма при заданных начальных значениях   ,   ,   вычисляется последовательность оценок   , используемых в расчетах прогнозных серий   ,   по   значений в каждой. Определенные таким образом серии прогнозных расчетов используются далее для расчета величины выбранного критерия   . Все полученные значения критерия (их число определяется количеством узлов сетки) сравниваются между собой, что позволяет среди узлов   ,   (   – множество порядковых номеров, присвоенных узлам сетки) определить такой   , для которого   для всех   . Так определенный вектор параметров   считается оптимальным. Его точность определяется задаваемым при построении сетки шагом изменения настраиваемых параметров.

45. Многофакторная регрессионная модель с адаптивным механизмом

46. Дисперсионное отношение

47. Адаптивная многорегрессионная модель

48. Расстояние Махаланобиса

49. Взвешенное Евклидово расстояние. Евклидова метрика

Выбор метрики, или меры близости, является узловым моментом исследования, от которого в значительной степени зависит окончательный вариант разбиения объектов на классы при данном алгоритме разбиения. В каждом конкретном случае этот выбор должен производиться по-своему, в зависимости от целей исследования, физической и статистической природы наблюдений, априорных сведений о характере вероятностного распределения X.

Рассмотрим наиболее широко используемые в задачах кластерного анализа расстояния и меры близости.

Обычное евклидово расстояние определяется по формуле

 

где x_ij, х_kj — значения j-го признака у i-го (j-го) объекта (j= 1, 2, ..., m, i,j = 1, 2, .... п).

Оно используется в следующих случаях:

а) наблюдения берутся из генеральной совокупности, имеющей многомерное нормальное распределение с ковариационной матрицей вида σ²E_k, где Е_k — единичная матрица, т.е. исходные признаки взаимно независимы и имеют одну и ту же дисперсию;

б) исходные признаки однородны по физическому смыслу и одинаково важны для классификации.

 Естественное с геометрической точки зрения евклидово пространство может оказаться бессмысленным (с точки зрения содержательной интерпретации), если признаки измерены в разных единицах. Чтобы исправить положение, прибегают к нормированию каждого признака путем деления центрированной величины на среднее квадратическое отклонение и переходят от матрицы Хк нормированной матрице с элементами

где x_il — значение l-го признака у i-го объекта;

 — среднее значение l-го признака;

 — среднее квадратическое отклонение l-го признака.

Однако эта операция может привести к нежелательным последствиям. Если кластеры хорошо разделимы по одному признаку и не разделимы по другому, то после нормирования дискриминирующие возможности первого признака будут уменьшены в связи с усилением «шумового» эффекта второго.

Взвешенное Евклидово расстояние определяется из выражения

(15.5)

где - весовой коэффициент.

Оно применяется в тех случаях, когда каждой l-й компоненте вектора наблюдений Х удается приписать некоторый «вес» ω₁, пропорциональный степени важности признака в задаче классификации. Обычно принимают 0 ≤ ω_l  ≤ 1, где l = 1,2, ..., k.

Определение весов, как правило, связано с дополнительными исследованиями, например с организацией опроса экспертов и обработкой их мнений. Определение весов ω_l только по данным выборки может привести к ложным выводам.

50. Модели с аддитивными и мультипликативными составляющими

Временным рядом называется ряд наблюдаемых значений изучаемого показателя, расположенных в хронологическом порядке или в порядке возрастания времени.

Временные ряды могут содержать два вида компонент – систематическую и случайную составляющие.

Систематическая составляющая временного ряда является результатом воздействия постоянно действующих факторов.

Выделяют три основных систематических компоненты временного ряда:

1) тренд;

2) сезонность;

3) цикличность.

Модели, где временной ряд представлен в виде суммы перечисленных компонентов называются аддитивными, если в виде произведения – мультипликативными моделями.

Общий вид аддитивной модели следующий: Y = T + S + E. Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (T), сезонной (S) и случайной (E) компонент.

Общий вид мультипликативной модели выглядит так: Y = T * S * E. Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (T), сезонной (S) и случайной компонент (E). Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.

Построение аддитивной и мультипликативной моделей сводится к расчету значений трендовой, циклической и случайной компонент для каждого уровня ряда.

Процесс построения модели включает в себя следующие шаги:

1)Выравнивание исходного ряда методом скользящей средней.

2)Расчет значений сезонной компоненты.

3)Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных в аддитивной или мультипликативной модели.

4)Аналитическое выравнивание уровней и расчет значений тренда с использованием полученного уравнения тренда.

5)Расчет полученных по модели значений.

6)Расчет абсолютных и относительных ошибок.

Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок для анализа взаимосвязи исходного ряда и других временных рядов.

51. Логистическая кривая Перла-Рида

Логистическая кривая (кривая Перла-Рида), имеющая асимптоту, применяется, когда существует ограничение на рост показателя (уровней динамического ряда).

Логистическая кривая, или кривая Перла - Рида, - возрастающая функция, наиболее часто выражаемая в виде

 

другие виды этой кривой:

В этих выражениях а и b - положительные параметры; k - предельное значение функции при бесконечном возрастании времени.

Если взять производную данной функции, то можно увидеть, что скорость возрастания логистической кривой в каждый момент времени пропорциональна достигнутому уровню функции и разности между предельным значением k и достигнутым уровнем. Логарифм отношения первого прироста функции к квадрату ее значения (ординаты) есть линейная функция от времени.

Конфигурация графика логистической кривой близка графику кривой Гомперца, но в отличие от последней логистическая кривая имеет точку симметрии, совпадающую с точкой перегиба.

52. Кривая Гомпертца

Кривая Гомперца имеет аналитическое выражение:

где а, b - положительные параметры, причем b меньше единицы; параметр k - асимптота функции.

В кривой Гомперца выделяются четыре участка: на первом - прирост функции незначителен, на втором - прирост увеличивается, на третьем участке прирост примерно постоянен, на четвертом - происходит замедление темпов прироста, и функция неограниченно приближается к значению k. В результате конфигурация кривой напоминает латинскую букву S.

Логарифм данной функции является экспоненциальной кривой; логарифм отношения первого прироста к самой ординате функции - линейная функция времени.

На основании кривой Гомперца описывается, например, динамика показателей уровня жизни; модификации этой кривой используются в демографии для моделирования показателей смертности и т.д.