2.5 Уравнения Бернулли для струйки и потока реальной жидкости

В отличие от идеальной жидкости при движении реальной жидкости часть энергии, которой она располагает, расходуется на преодоление гидравлических сопротивлений. Поэтому начальная общая энергия жидкости не остается постоянной по длине струйки или потока, а уменьшается от сечения к сечению. При этом происходит необратимое преобразование гидромеханической энергии в тепловую форму. Тогда уравнение Бернулли для реальной жидкости должно учитывать энергию, затраченную на преодоление гидравлических сопротивлений h_n. Эту составляющую вносят в правую часть уравнения. Уравнение запишется в виде:

.

При выводе этого уравнения принято, что скорости движения отдельных частиц жидкости в пределах живого сечения одинаковы и равны средней скорости. Однако если обратиться к потоку реальной жидкости, то необходимо учесть, что скорости в разных точках живого сечения потока не одинаковы вследствие действия сил трения, за счет чего происходит торможение жидкости у стенок, и поле скоростей изменяется (рис. 29).

Рисунок 29 − Распределение скоростей в живом сечении идеальной и реальной жидкости

Подсчитав энергии потока, выразим интеграл кинетической энергии через среднюю скорость.

,

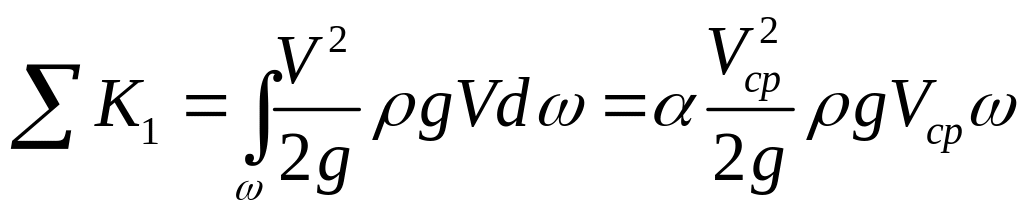где − коэффициент Кориолиса, учитывающий, что кинетическая энергия потока, подсчитанная по средней скорости в сечении V_cp, не равна сумме кинетических энергий элементарных струек , подсчитанной по действительным скоростям V, и выражает отношение этих величин:

.

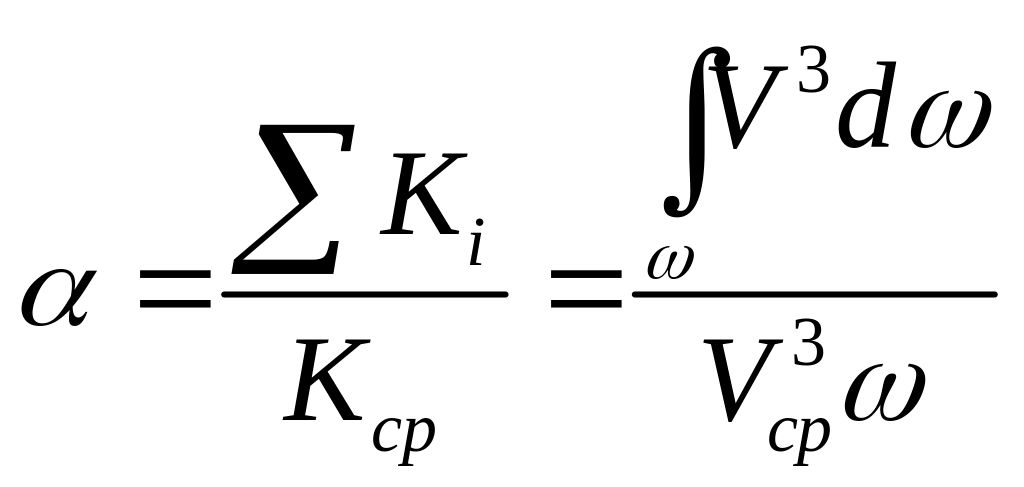Для ламинарного режима , для турбулентного α=1,02 - 1,12.

С учетом сказанного уравнение Бернулли для потока имеет вид:

.

Уравнение Бернулли имеет геометрический и энергетический смысл.

Энергетический смысл: каждый из членов уравнения выражает величину удельной энергии потока, т. е. энергию, приходящуюся на единицу массы движущейся жидкости:

• z − удельная потенциальная энергия положения,

• p/ρg − удельная потенциальная энергия давления,

• z +p/ρg − удельная потенциальная энергия,

• V²/2g − удельная кинетическая энергия,

• h_n − потери удельной энергии.

Сумма всех составляющих − полная удельная энергия. Следовательно, энергетический смысл можно выразить так: при установившемся движении потока реальной жидкости сумма четырех удельных энергий остается неизменной вдоль потока.

Геометрический смысл: каждый из членов уравнения выражает высоту (напор), что легко доказать проанализировав размерность каждого члена:

• z − геометрический напор [z] = м,

• p/ρg − пьезометрический напор [p/ρg] = (Н/м²) / (Н/м³) = м,

• z +p/ρg − гидростатический напор,

• V²/2g − скоростной напор [V²/2g] = (м²/с²)/ (м/с²) = м,

• h_n − потери напора [h_n] = м.

Сумма всех составляющих − полный напор.

Рассмотрим построение пьезометрической и напорной линии для случая реальной жидкости. При построении пьезометрической и напорной линии для потока реальной жидкости необходимо учитывать не только взаимную трансформацию потенциальной и кинетической энергий, но и убывание полной энергии по длине потока из-за потерь напора. Расположим в нескольких сечениях пьезометрические и гидродинамические трубки. Соединим уровни жидкости в пьезометрах, получим пьезометрическую линию. А соединив уровни жидкости в гидродинамических трубках, получим напорную линию. Напорная линия по длине потока реальной жидкости всегда понижается из-за потерь (рис. 30). Падение напорной линии на единицу длины называется гидравлическим уклоном i и характеризует величину потерь напора на единицу длины.

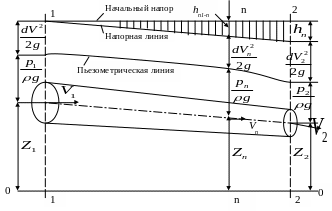
Рисунок 30 − Пример построения пьезометрической и напорной линии для реальной жидкости