17. Линейное неоднородное дифференциальное уравнение (лнду). Отыскание частного решения в случае с квазиполиномом.

Структура общего решения ЛНДУ 2-го порядка :

y’’ + (x) y’ + (x) y = f (x) (5.1) - ЛНДУ (x) , (x) С (a, b) - непрерывная функция

y’’ + (x) y’ + (x) y = 0 (5.2) - соответствующее однородное уравнение

Теорема (5.1) структура общего решения ЛНДУ

Общее решение уравнение (5.1) является сумма его произвольного частного решения и общего решения

= y = (5.3) Доказательство:

y = + y’ = ( ) ‘ + ’ y’’ = ( ) ‘’ + ’’ y’’ = ( ) ‘’ + ’’ + (x) ( )’ ’ + (x) ( + ) = f (x)’ ( ) ‘’ + (x) ( )’ + (x) ( ) + + (x) + (x) ) + ( ’’ + (x) ’ + (x) =f(x,y) y= + (5.4)

Для этого нужно доказать, что из решения (5.4) можно выделить единственную частное решение удовлетворяющее начальным условиям. Дифференцируем (5.4) и подставляем условия (5.5) y ( ) = y ‘( ) = (5.5)

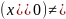= W 0 ! ,

Интегрирование ЛНДУ 2-го порядка и правой частью специального вида:

Рассмотрим ЛНДУ 2-го порядка с постоянными коэффициентами : y’’ + p y’ + q y = f(x) (5.7)

Можно искать частное решение методом Лагранжа, однако можно найти проще. Рассмотрим эти случаи:

f(x) =

f(x) = ( cos b x + (x) sin b x)

Квазиполином Эйлера

В этих случаях записываем ожидаемую форму решения с неопределенными коэффициентами и подставляем в уравнение (5.1) Из получения тождества находим значения коэффициентов

Случай 1 : правая часть (5.7) имеет вид : f(x) = α R y’’ + p y’ + q y = (5.8)

В этом случае : = Qn (x) (5.9)

Где n – число = кратности α как корня характеристического уравнения. При этом Qn (x) = x ‘’ + + …. + A ‘’ Ai (i= 0, 1, 2,…) А) Пусть α – не является корнем характеристического уравнения:

+ p k + q = 0 α r = 0 = Q u (x) *

Б) Пусть α является 2-ух однократным корнем характеристического уравнения:

α = + p k + q = 0 r = 1 = * Q n (x) *

В) Пусть α является 2-ух кратным корнем характеристического уравнения :

α = + p k + q = 0 r = 2 = * Q n (x) *

Случай 2:

Правая часть (2.7) или вид:

f(x) = ( ) cosβx + Q m (x) sin β (x )

Где )и Qm (x) многочлен степени nиm соответствуют α и β действительного числа

Уравнение (5.7) тогда запишется в виде

y’’ + py’ + qy = ( ) cosβx + Qm (x) sinxβ ) (5.10)

= * * (Me (x) * cosβx + Ne (x) * sin βx ) (5.11)

r-число равное кратности (α + βi) как корня уравнения :

+ pk + q = 0 Многочлены степени е с неопределенным коэффициентом Me (x)Ne (x) е - max (n, m)

Замечание 1 :После подстановки функции из (5.11) в (5.10) приравниваем многочлен перед одноименной тригонометрической функциейв левой и правой частях уравнения

Замечание 2 : Формула (5.11) сохраняется и при ) 0 или + Qm (x) 0

Замечание 3 : Если правая часть уравнения (5.7) есть сумма вида 1 или 2 то для нахождения используется теорема (5.2)

Интегрирование ЛНДУ п-го порядка (n постоянным коэффициентом и правой частью специального вида

Рассмотрим линейное неоднородное дифференциальное уравнениеn-го порядка

+ (x) + (x) + … + (x)y = (x) , …, (x) , f(x) , x (а, в) = f(x)

+ (x) + … + (x)y = 0

Теорема (5.3) : ( О структуре общего решения ЛНДУ n-го порядка)

Общее решение yЛНДУ n-го порядка = сумме частного решения НУ и общего решения ОУ y=

может быть найдено если известно общее решение ОУ

= + + … +

y(x) – частное решение образующее фундаментальную систему решений ОУ

+ + … + = 0 + + … + = 0 + + … + = 0

+ + … + = f (x)

Однако для ЛНДУ n-го порядка с постоянными коэффициентами, правая часть f(x) которая имеет специальный вид, можно найти методом неопределенных коэффициентов

Метод подбора частного решения для уравнения:

y’’ + + … + y = f (x) R