7.Уравнение в полных дифференциалах.

Дифференциальное уравнение вида , называется уравнением в полных дифференциалах, если существует такая функция двух переменных u(x,y) с непрерывными частными производными, что справедливо выражение :

Общее решение уравнения в полных дифференциалах определяется формулой где C − произвольная постоянная.

Необходимое и достаточное условие

Пусть функции P(x,y) и Q(x,y) имеют непрерывные частные производные в некоторой области D. Дифференциальное уравнение P(x,y)dx + Q(x,y)dy = 0 будет являться уравнением в полных дифференциалах тогда и только тогда, если справедливо равенство:

Алгоритм решения уравнения в полных дифференциалах:

1. Сначала убедимся, что дифференциальное уравнение является уравнением в полных дифференциалах, используя необходимое и достаточное условие:            

2. Затем запишем систему двух дифференциальных уравнений, которые определяют функцию u(x,y):

           

3. Интегрируем первое уравнение по переменной x. Вместо постоянной C запишем неизвестную функцию, зависящую от y:            

4. Дифференцируя по переменной y, подставим функцию u(x,y) во второе уравнение:   

Получим:            

5. Интегрируя последнее выражение, находим функцию φ(y) и функцию u(x,y):            

6. Общее решение уравнения в полных дифференциалах записывается в виде:

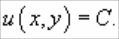
8. Уравнения, допускающие интегрирующий множитель.

Для того чтобы левая часть уравнения (2.8) является полным дифференциалом некоторой функции U (x , y) необходимо и достаточно условие Эйлера

(2.10)

dU(х,у)=

Если условие Эйлера выполняется, то уравнение (2.8) легко интегрировать

dU = Mdx + Ndy

dU=

При вычиcлении интеграла величина у рассматривается как const , поэтому c(y) является произвольной функцией y. Для определения функции C(y) дифференцируем найденную функцию U(x, y) по y и так как , получим:

(

В некоторых случаях, когда левая часть уравнения (2.8) не является полным дифференциалом, легко удается подобрать функцию после умножения на которую левая часть уравнения (2,8) превращается в полный дифференциал, то есть dU = Mdx + Ndy и в этом уравнение эти функции удовлетворяют условию Эйлера.

Такая функция µ называется интегрируемым множеством. Заметим, что умножение может привести к появлению посторонних решений , обращающих µ(x, y) в 0

В общем случае не всегда так легко удаётся найти интегрир. множитель.

Вообще, надо подобрать хотя бы одно ненулевое решение уравнения:

(2.11)

Вообще задача интегрирования (2.11) ничуть не проще задачи интегрирования (2.10)

Однако, если мы можем считать µ функцией только одной переменной будь то x, y, х²+у² и т.д., то задача существенно упрощается .

Например, найдём условие, когда µ можно найти как функцию от х

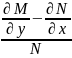; считаем это выражение непрерывной функцией х.

Проинтегрируем и получим

Ln µ =

M= C * 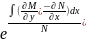(2.12)

Можно считать c=1, так как нам нужен хотя бы один интегрирующий множитель

Если является функцией только x, то интегрирующий множитель найдется по формуле(2.12)

Аналогично можно выписать условие при которых интегрирующий множитель зависит от другой выбранной переменной.