1. Виды дифференциальных уравнений. Интеграл дифференциального уравнения. Общий интеграл. Интегральная кривая.

При изучении химии, физики, экологии, экономики, биологии и иных явлений, часто возникает уравнения связывающие неизвестную функцию и ее производные. Такие уравнения называются дифференциальными уравнениями.

dx/dt=-kx—уравнение радиоактивного распада, где k-постоянная распада, x-количество неразложившегося вещества в момент времени t. Скорость распада dx/dt пропорц. количеству нераспавшегося вещества. 2) —Уравнение движения точки массой m под действием силы F ,

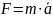
3) Нахождение неизвестных функций, определяемых дифференциальными уравнениями, является основной задачей теорий дифференциальных уравнений. Если в дифференциальном уравнении неизвестные функция является функциями одной переменной, то дифференциальное уравнение называется обыкновенным. Например уравнения 1 и 2. Если неизвестная функция зависит от двух и более переменных, то уравнение называется уравнением частных производных. Например уравнение 3. Порядком дифференциального уравнения называется максимальный порядок, входящий в уравнение производной неизвестной функции. Решением дифференциального уравнения называется функция, которая при подстановке в дифференциальное уравнение, обращает его в тождество.

Например уравнение радиоактивного распада: dx/dt=-kx (1.1) (1.2)

где c- произвольная постоянная

Уравнение (1.1) не вполне определяет закон распада x=x(t).

Нужно также знать количество вещества x( в момент времени . Тогда закон Распада примет вид:

x=

Процесс нахождения решений дифференциальных уравнений, называется интегрированием дифференциальных уравнений. Не всегда решение находится в явном виде, как в этом примере.

Однако, используя компьютеры, можно решить уравнение приближенно с большой точностью.

Пусть математическая точка массой m движения под действием силы F:

Уравнение движения примет вид: m = F(t, (1,3)

Для нахождения закона движения (t)необходимо знать начальное положение точки и скорость: ( = (1.4)

( ) = (1.5)

Задача нахождения (t) при заданных начальных условиях (1.4) и (1.5) называется задачей Коши.

Вектор уравнения 2-ого порядка (1.3) можно переписать в виде системы 2-ух векторных уравнений 1-го порядка, если рассмотреть скорость как вторую неизвестную формулу:

(1.6)

Каждое векторное уравнение в трёхмерном пространстве может быть заменено системой из 3-х скалярных уравнений для проекции векторов на оси координат. При интегрировании дифференциального уравнения обычно ставят цель найти все его решения. Например: в уравнение (1.1) все решения получаются из решения (1.2) при некотором выборе постоянной C. Решение (1.2) – общее решение уравнения (1.1) Решения дифференциального уравнения , получившиеся из общего решения называется частными. Однако иногда не удаётся включить в общее решение все решения уравнения. Решения, не являющиеся частными, называются особыми. Говорят, что для дифференциального уравнения поставлена задача, если заданы некоторые дополнительные условия. В простейшем случае задаются начальные значения искомой функции и её производных. То есть, ставится задача Коши. Например: в задаче (1.1) задаётся начальное количество вещества . Не всегда удаётся найти решение в явном виде y=y(x) Иногда оно задаётся неявно соотношением Ф (x,y)=0 , наз. интегралом уравнения. Соответственно при неявном задании общего решения уравнения, получается общий интеграл уравнения Ф (x,y,с)=0

Рассмотрим уравнение 1-го порядка y’=f(x,y) (1.7)разрешённого относительно 1-ой производной. Пусть функция f(x,y) имеет некоторую область определений D область из ,которая также является областью определения уравнения (1.7) Обычно предполагается, что f непрерывна в D Функция y= (x) , x [a,b] , непрерывная и непрерывно дифференцируема на [a,b] такая, что точка (x, у(x)) D при x [a,b] и при этом выполняется равенство ‘ (x)= f (x , (x)) , x [a, b] называется решением уравнения (1.7) на [a, b]

Пример 5. = 3 = 3 y * = 3 y + c =3x y=

Областью определения является вся плоскость . Заметим, что это уравнение имеет решение y(x)=0,которое нельзя получить из общего решения при выборе константы C. Это решение является особым. Геометрическое решение уравнения (1.7) y= (x) соответствует линия, лежащая в области D в плоскости и представляющая собой график функции (x). Эта линия называется интегральной линией уравнения (1.7) Так как функция (x) имеет непрерывную производную (x) интегральная линия имеет в каждой точке (x , (x)) касательную, угловой коэффициент которой определяется из уравнения (x) =f (x, (x)) Очевидно угловой коэффициент можно вычислить в любой точке (x,y) D не находя самой интегральной кривой. Выбрав направляющий вектор касательной, сопоставим каждой точке области D некоторый ненулевой вектор. Так в области D получим поле направлений. И так уравнению (1.7) соответствует в области D векторное поле касательных направлений. Задача решения этого уравнения имеет следующую геометрическую интерпретацию: через каждую точку области D требуется провести кривую называемую интегральной, касательная которой в каждой точке определяется векторным полем уравнения (1.7) Заметим, что общему решению соответствует семейство кривых, а решению задачи Коши - интегральная кривая, проходящая через точку ( , ) D

При геометрическом решении уравнения (1.7) можно воспользоваться методом изоклин.

Изоклином называется некоторое геометрическое место точек, в каждой точке которого векторное поле задаёт параллельное направление. f(x, y)= k=const Различным значениям K соответствуют различные изоклины. B точках пересечения с изоклинами интегральная линия имеет касательную с угловым коэффициентом K.