Задание 5

1. Проверим идентификацию каждого уравнения и системы в целом.

Модель имеет три эндогенные ( , , ) и три экзогенные ( , , ) переменные.

Проверим каждое уравнение системы на необходимое (Н) и достаточное (Д) условия идентификации.

Первое уравнение.

Н: эндогенных переменных – 2 ( , ),

отсутствующих экзогенных – 1 ( ).

Выполняется необходимое равенство: 1 + 1 = 2, следовательно, уравнение точно идентифицируемо.

Д: в первом уравнении отсутствуют и . Построим матрицу из коэффициентов при них в других уравнениях системы:

Уравнение	Отсутствующие переменные
Второе	-1
Третье		0

Вычислим определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в первом уравнении:

.

Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и первое уравнение точно идентифицируемо.

Второе уравнение.

Н: эндогенных переменных – 3 ( , , ),

отсутствующих экзогенных – 2 ( , ).

Выполняется необходимое равенство: 2 + 1 = 3, следовательно, уравнение точно идентифицируемо.

Д: во втором уравнении отсутствуют и . Построим матрицу из коэффициентов при них в других уравнениях системы:

Уравнение	Отсутствующие переменные
Первое
Третье

Вычислим определитель матрицы, составленной из коэффициентов при переменных, отсутствующих во втором уравнении:

.

Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и первое уравнение точно идентифицируемо.

Третье уравнение.

Н: эндогенных переменных – 2 ( , ),

отсутствующих экзогенных – 1 ( ).

Выполняется необходимое равенство: 1 + 1 = 2, следовательно, уравнение точно идентифицируемо.

Д: в первом уравнении отсутствуют и . Построим матрицу из коэффициентов при них в других уравнениях системы:

Уравнение	Отсутствующие переменные
Второе	-1	0
Третье

Вычислим определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в третьем уравнении:

.

Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и первое уравнение точно идентифицируемо.

Таким образом, исследуемая система точно идентифицируема и может быть решена косвенным методом наименьших квадратов.

2. Найдем приведенную форму модели.

(1)

Подставим первое уравнения системы (1) во второе и получим:

,

. (2)

Уравнение (2) подставим в третье уравнение системы (1) и выразим :

,

(3)

В первое уравнение системы (1) подставим уравнение (3) и выразим :

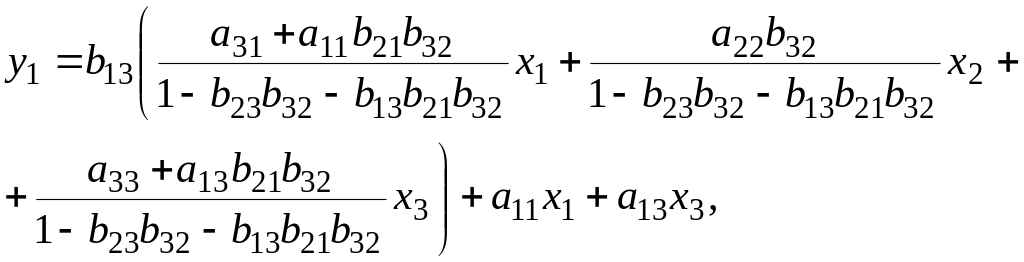
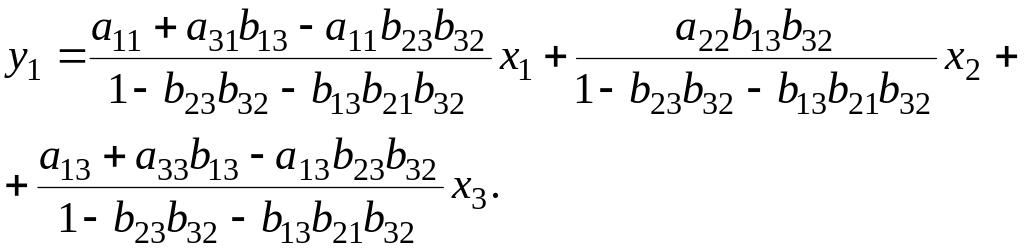
Уравнение (3) подставим в (2) и выразим :

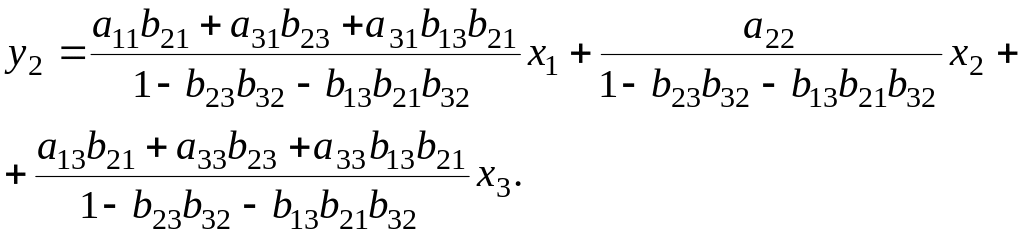
Таким образом, приведенная форма модели имеет вид:

где

, ,

, ,

, ,

, ,

.