Задание 2
Xi |
1 |
1 |
1 |
2 |
2 |
2 |
3 |
3 |
3 |
2 |
Yi |
3 |
5 |
5 |
5 |
8 |
9 |
5 |
9 |
9 |
7 |
Для расчетов параметров уравнения линейной регрессии строим расчетную таблицу 2.
Таблица 2
|
x |
y |
xy |
x2 |
y2 |
yx |
y-yx |
(y-yx)2 |
1 |
1 |
3 |
3 |
1 |
9 |
4,8333 |
-1,8333 |
3,3611 |
2 |
1 |
5 |
5 |
1 |
25 |
4,8333 |
0,1667 |
0,0278 |
3 |
1 |
5 |
5 |
1 |
25 |
4,8333 |
0,1667 |
0,0278 |
4 |
2 |
5 |
10 |
4 |
25 |
6,5000 |
-1,5000 |
2,2500 |
5 |
2 |
8 |
16 |
4 |
64 |
6,5000 |
1,5000 |
2,2500 |
6 |
2 |
9 |
18 |
4 |
81 |
6,5000 |
2,5000 |
6,2500 |
7 |
3 |
5 |
15 |
9 |
25 |
8,1667 |
-3,1667 |
10,0278 |
8 |
3 |
9 |
27 |
9 |
81 |
8,1667 |
0,8333 |
0,6944 |
9 |
3 |
9 |
27 |
9 |
81 |
8,1667 |
0,8333 |
0,6944 |
10 |
2 |
7 |
14 |
4 |
49 |
6,5000 |
0,5000 |
0,2500 |
Итого |
20 |
65 |
140 |
46 |
465 |
65,0000 |
0,0000 |
25,8333 |
Среднее значение |
2,0000 |
6,5000 |
14,0000 |
4,6000 |
46,5000 |
|
|
|
|
0,7746 |
2,0616 |
|
|
|
|
|
|
|
0,6000 |
4,2500 |
|
|
|
|
|
|
Вычислим оценки коэффициентов регрессии:
,
.
Получено уравнение
регрессии:
.
С увеличением количества продавцов на
1 чел. количество проданных автомобилей
возрастает в среднем на 1,6667 машин.
Тесноту линейной связи оценит коэффициент корреляции:
.
Оценку статистической значимости параметров регрессии проведем с помощью t-статистики Стъюдента.
Выдвигаем гипотезу
о статистически незначимом отличии
показателей от нуля.
для числа степеней
свободы
и
составит 2,3060 (приложение 2).
Определим случайные
ошибки
,
,
:
,
,
,
.
Тогда
,
,
.
Так как
,
то гипотеза
не отклоняется и признается случайная
природа формирования
,
или
.
Проведем анализ дисперсии зависимой переменной.
Остаточная сумма
квадратов отклонений
исходя из таблицы 2 равна 25,8333,
а сумма квадратов отклонений, обусловленная
регрессией, вычисляется по формуле:
Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака Y характеризует коэффициент детерминации:
.
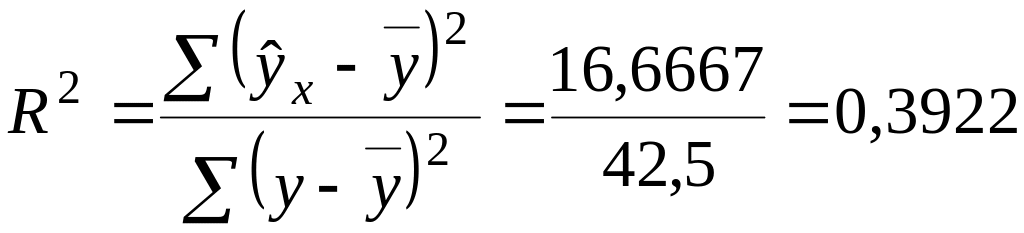Это означает, что 39% вариации количества проданных автомобилей (Y) объясняется вариацией фактора X – количества продавцов.
Проверим на уровне значимости 5% гипотезу о линейной зависимости числа продаж от числа продавцов с помощью F-критерия Фишера.
Выдвигаем гипотезу о статистической незначимости уравнения регрессии и показателя тесноты связи.
для уровня значимости
и
,
составит 5,32 (приложение 1).
.
Так как
,
то гипотеза
не отклоняется. Этот результат можно
объяснить невысокой теснотой выявленной
зависимости и небольшим числом наблюдений.