53. Выберите предикат: а) (верно) б) Разделить на х в) г) Все простые числа нечетны

54. Выберите истинное высказывание:

    1. 

    2. (Верно)

    3. 

    4. 

55. Установите соответствие

1) Квантор общности	А)
2) Квантор существования	В)
3) Ограниченный квантор общности	С)
4) Ограниченный квантор существования	D)
	E)

Ответ: 1-С; 2-А; 3-В; 4-D

56. Множество истинности предиката , заданного на множестве

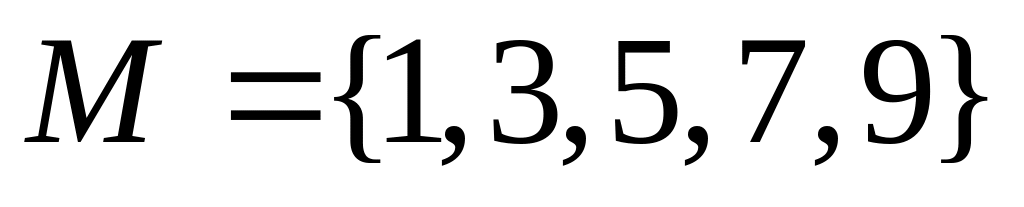
1) 2)

3) (Верно) 4)

57. Множество истинности предиката , заданного на множествах

1) 2) (Верно)

3) 4)

58. Укажите тождественно истинный предикат

    1. (Верно)

    2. 

    3. 

    4. 

59. Установите соответствие между предикатами и их множествами истинности

1)	А)
2)	В)
	С)
	D)

Ответ: 1-С; 2-В

60. Для тождественно предиката , заданного на множествах установите соответствие

1) Тождественно истинный предикат	А)
2) Тождественно ложный предикат	В)
3) Выполнимый предикат	С)
4) Опровержимый предикат	D)
	E)

Ответ: 1-В; 2-А; 3-D; 4-E

61. Установите соответствие

1) Тождественно истинный предикат	А)
2) Тождественно ложный предикат	В)
3) Выполнимый предикат	С)
	D)

Ответ: 1-D; 2-A; 3-B

62. Упорядочить предикаты по количеству свободных переменных

1) 2)

3) 4)

Ответ: с; а; b; d

63. Установите соответствие

1) Предикаты P и Q – равносильны	А)
2) Предикат Q является следствием предиката Р	В)
	С)
	D)

Ответ: 1-С; 2-А

64. Установите соответствие между равносильными предикатами

1)	А)
2)	В)
	С)

Ответ: 1-В; 2-С

65. Укажите пару предикатов, равносильных на множестве Z

1) , 2) ,

3) , (верно) 4) ,

66. Выберите множество так, чтобы над ним предикаты «х – простое число», «х – четное число» были равносильны

    1. Множество натуральных числе

    2. Множество четных чисел

    3. Множество простых чисел

    4. (верно)

    5. 

67. Следствием предиката , заданного на множестве целых чисел является предикат, заданный на множестве целых чисел

1) (верно) 2)

3) 4)

68. Из приведенных выражений выберите формулу логики предикатов

1) 2) (верно)

3) 4)

69. Если формула логики предикатов содержит только операции конъюнкции, дизъюнкции и кванторные операции, а операция отрицания отнесена к элементарным формулам, то говорят, что она имеет …

1) Нормальную форму (верно) 2) Совершенную нормальную форму

3) Предваренную нормальную форму 4) Общезначимую форму

70. Если в нормальной форме формулы логики предикатов кванторные операции или отсутствуют, или используются после всех операций алгебры высказываний, то говорят, что она имеет …

    1. Нормальную форму

    2. Совершенную нормальную форму

    3. Предваренную нормальную форму (верно)

    4. Общезначимую форму

71. Формула логики предикатов называется общезначимой, если

    1. Существует область, на которой эта формула выполнима

    2. Она принимает истинные значения для всех значений переменных, входящих в эту формулу и отнесенных к конкретной области М

    3. Она тождественно истинная на всякой области (верно)

    4. Она выполнима на всякой области

Математические теории

72. Длина слова 010001 в алфавите равна …

Ответ: 6

73. Пусть T – некоторая теория. Пару , состоящую из алфавита и множества выражений теорииТ называют …

    1. Языком теорииТ (верно)

    2. ТеориейТ

    3. Алфавитом теорииТ

    4. Множеством выражений теорииТ

74. Конечная последовательность 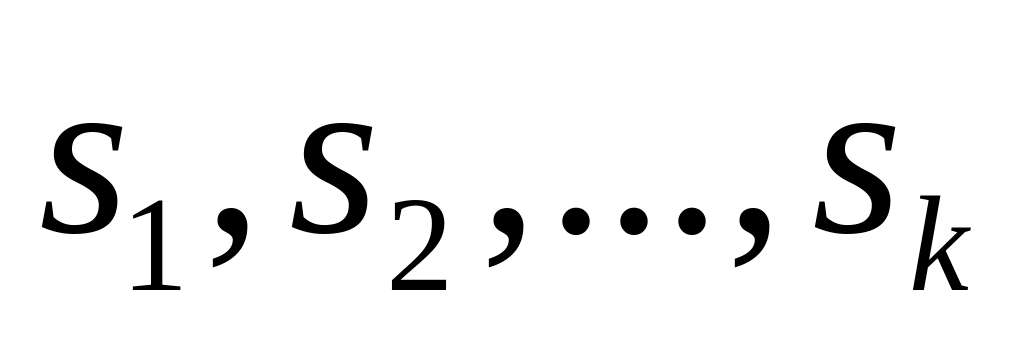высказываний рассматриваемой теории, каждое из которых либо является аксиомой, либо выводится из одного или более предыдущих высказываний этой последовательности по логическим правилам вывода называется …

Ответ: доказательством (доказательств#$#)