реферат

Технічний коледж національного університету

“Львівська політехніка”

Реферат

На тему:” Логіка мінімізації булевих функцій”

Виконав:

Студент 31КІ

Кобринович Р. В.

Викладач:

Ногач М. М.

Львів 2019

Зміст

Логіка мінімізації булевих функцій

Способи мінімізації

1.Аналітичний спосіб мінімізації

2.Метод Блейка-Порецького

3.Метод Нельсона

4.Метод дужкових форм

5.Метод карт Карно

Література

Логіка мінімізації булевих функцій

Мінімізація (спрощення форми запису) функції є важливою операцією при синтезі логічної схеми, так як завдяки попередньо проведеній мінімізації схема реалізується з найменшим числом елементів.

Метою мінімізації є зменшення вартості технічної реалізації логічних функцій незалежно від використовуваних апаратних засобів.

Виявити і виділити надлишковість в записі функції можливо шляхом перетворень з використанням аксіом, законів, тотожностей та теорем алгебри логіки. Однак такі перетворення потребують громіздких викладок і пов’язані з великою витратою часу.

Логічні функції апаратно реалізуються за допомогою мікросхем, орієнтованих на виконання тих чи інших операцій. Мікросхеми загального використання у більшості випадків можуть реалізовувати кілька простих одиночних операцій.

Тому справедливо стверджувати, що, чим простіше аналітична форма запису логічної функції, тим менше використовується логічних елементів і, як результат, тим менше мікросхем необхідно для її реалізації. Складність логічних функцій визначається кількістю логічних змінних, які входять до їхнього складу в прямому й інверсному вигляді, та кількістю простих логічних операцій над ними.

Будь-яка логічна функція може записуватися різними аналітичними виразами різного рівня складності. Серед них є такі, які містять мінімальну кількість логічних змінних і операцій над ними. Задача знаходження таких аналітичних виразів називається мінімізацією логічних функцій.

Для мінімізації функції з числом змінних до п’яти-шести найбільш зручними є два методи: метод Квайна і метод карт Карно.

Задача мінімізації – це задача неоднозначна, і розв'язуючи її різними способами, можна отримати різні вирази мінімізованої функції, які відрізнятимуться між собою кількістю змінних і операцій над ними.

Способи мінімізації

1. Аналітичний спосіб мінімізації.

Для зменшення складності логічних функцій найчастіше використовують операції склеювання:

та поглинання:

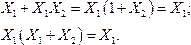
Як приклад розглянемо процедуру спрощення такої функції:

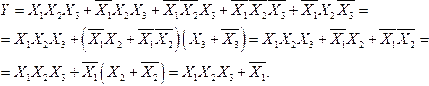
Одержана функція має мінімальну складність.

2. Метод Блейка-Порецького

Метод дозволяє отримувати скорочену ДНФ булевої функції f з її довільної ДНФ. Базується на застосуванні методу загального склеювання Ax v Bẍ = Ax v Bẍ v AB, правильність якого легко доводиться: Ax = Ax v ABx; Bẍ = Bẍ v ABẍ. З цього слідує: Ах v Вẍ = Ах v АВх v Вẍ v АВẍ = Ах V Вẍ V АВ. В основу методу покладено наступне твердження: якщо в випадковій ДНФ булевій функції f зробити всі можливі узагальнені склеювання, а потім виконати всі поглинання, то в результаті вийде скорочена ДНФ функція f.

Приклад: Булева функція f задана випадковою ДНФ: f = ẍ1ẍ2 v x1ẍ2ẍ3 v x1x2. Знайти методом Блейка — Порецкого скороченну ДНФ функцїї f. Проводимо узагальнені склеювання. Легко бачити, що перший і другий елемент заданої ДНФ допускають узагальнене склеювання по змінній х1. В результаті склеювання маємо:

ẍ1ẍ2 v x1ẍ2ẍ3 = ẍ1ẍ2 v x1ẍ2ẍ3 v ẍ2ẍ3

Перший і третій елемент вихідної ДНФ допускають узагальнене склеювання як по змінній х1, так і по х2. Після склеювання по x1 маємо:

ẍ1ẍ2 v x1x2 = ẍ1ẍ2 v x1x2 v ẍ2x2 = ẍ1ẍ2 v x1x2.

Після склеювання по x2 маємо:

ẍ1ẍ2 v x1x2 = ẍ1ẍ2 v x1x2 v ẍ1x1 = ẍ1ẍ2 v x1x2 .

Другий і третій елемент ДНФ допускають узагальнене склеювання по змінній х2 . Після склеювання отримуємо :

x1ẍ2ẍ3 v x1x2 = x1ẍ2ẍ3 v x1x2 v x1x3 .

Виконавши останнє узагальнене склеювання, приходимо до ДНФ :

f = ẍ1ẍ2 v x1ẍ2ẍ3 v ẍ2ẍ3 v x1x2 v x1ẍ3 .

Після виконання поглинань отримуємо :

f = ẍ1ẍ2 v ẍ2ẍ3 v x1x2 v x1ẍ3 .

Спроби подальшого застосування операції узагальненого склеювання і поглинання не дають результату. Отже, отримана скорочена ДНФ функції f. Далі завдання пошуку мінімальної ДНФ вирішується за допомогою імплікаційної матриці точно так само, як у методі Квайна."

3. Метод Нельсона

Метод дозволяє отримати скорочену ДНФ булевої функції f з її випадкової КНФ. Якщо у довільній КНФ булевої функції розкрити всі дужки і провести всі поглинання, то в результаті буде отримана скорочена ДНФ булевої функції.

Приклад:

f = (x1 v ẍ2)(ẍ1 v x3)(x1 v x2 v ẍ3)

f = (x1x3 v ẍ1ẍ2 v ẍ2x3)((x1 v x2 v ẍ3))=

Знайдемо скорочену ДНФ: = x1x3 v x1x2x3 v ẍ1ẍ2ẍ3 v x1ẍ2x3

Зробимо поглинання: f = x1x3 v ẍ1ẍ2ẍ3 і виходить скорочена ДНФ.

4. Метод дужкових форм

Якщо розглядати схемну реалізацію булевих функцій, представлених у вигляді ДНФ або КНФ, то, без урахування інверсій, вони представляють собою дворівневі схеми І-АБО (АБО-І). Але в реальній схемотехніці подібні схеми зустрічаються досить рідко. Зазвичай загальні частини різних імплікант на основі дистрибутивного закону "виносяться за дужки", в результаті чого виходить багаторівнева схема, аналітичний запис якої прийнято називати дужковою формою (ДФ). Іноді в літературі операція "винесення за дужки" називається факторизацією або виділенням загальних частин. В даному підрозділі описується структура і отримання дужкових форм булевих функцій на основі ДНФ, але абсолютно аналогічні викладки застосовні і до КНФ. Наприклад, для функції чотирьох змінних f (11, 13, 14, 15) = 1, ДНФ має вигляд f = x1x2x3 v x1x2x4 v x1x3x4. Якщо в перших двох імплікантах винести за скобки x1x2, то отримаємо дужкову форму f = x1x2 (x3 v x4) v x1x3x4, котра містить на дві букви (два входи) менше, ніж вихідна ДНФ. Даній дужковій формі відповідає трирівнева схема. Для безпосереднього запису ДФ булевої функції зазвичай використовують першу формулу розкладання:

f (x1, x2, ...xi,... xn) = ẍi • f (x1, x2, ...0, ... xn) v xi • f (x1, x2, ...1,... xn);

Для наочності часто використовують графічну форму представлення розкладання по змінній xi. При цьому кожне розкладання по змінної xi є вузол граф-схеми, всередині якого записується змінна, по якій проводиться розкладання. Нижнє ліве ребро (позначається "0") відповідає функції f^(ẍi), а нижнє праве ребро (позначається "1") - функції f^(xi). Вихід вузла (верхнє ребро) відповідає результуючої функції f(xi). При цьому якщо f є деякий булевий вираз, то його доцільно укладати в дужки. Звідси і випливає результуюче вираз у вигляді ДФ. Мінлива xi називається суттєвою для функції f, якщо f^(ẍi) ≠ f^(xi). В іншому випадку змінна вважається фіктивною. Нижче показана графічна інтерпретація розкладання функції f по змінній xi і запис результуючого виразу. Нижні ребра вузла (вершини) графа (на малюнку помічені 0 і 1), зазвичай називаються вхідними, а верхнє ребро – вихідним

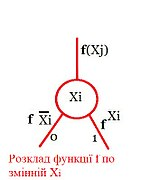
5. Метод карт Карно

Карта Карно (K-карта скорочено) - метод спрощення виразів булевої алгебри, зроблене Морісом Карно в 1953 поліпшення Діаграм Вейча, винайдених Едвардом Вейчем в 1952. Карта Карно зменшує потребу в обширних обчисленнях, використовуючи перевагу людської можливості розпізнання шаблонів, дозволяє швидке розпізнавання і виключення потенційних станів гонитви.

В карті Карно булеві змінні переносяться (зазвичай з таблиці істинності) і впорядковуються згідно з принципами кода Грея, в якому тільки одна змінна змінюється при переході між сусідніми квадратами. Коли таблиця згенерована, і у відповідні комірки записані вихідні значення, дані організовуються в найбільші можливі групи, що містять 2n комірок (n=0,1,2,3...)[1]. Далі, працюючи з цими групами, отримують мінімізовану ДНФ.

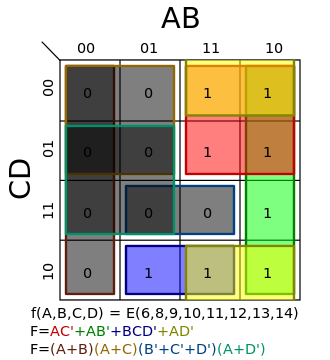
Література

Гаврилов Г. П.,Сапоженко А. А. Збірник завдань з дискретної математики. — М. : Наука, 1969.

Марченков С. С. Замкнуті класи булевих функцій. — М. : Фізматліт, 2000.

Яблонський С. В. Введення в дискретну математику. — М. : Наука, 1986.

Ігошин В. І. Математична логіка і теорія алгоритмів. — 2- е вид., Стереотип. — М., 2008. — 448 с. — ISBN 978-5-7695-4593-1.

Самофалов К. Г., Романкевич А. М., Валуйський В. Н., Канівський Ю. С., Пиневич М. М. Прикладна теорія цифрових автоматів. — Київ : Вища Школа, 1987. — С. 183-189.

Алексєєв В. Б. Дискретна математика (курс лекцій, II семестр). Упоряд. А. Д. Поспєлов

Бикова С. В., Буркатовський Ю. Б. , Булеві функції, навчально — методичний комплекс, Томськ, 2006