Расчёт теодолитного хода.

Абрис служит основным документом, по которым находятся на местности точки теодолитного хода.

А брис теодолитного хода

Изначально была задана точка (1) Х=200м ; Y=100м и дирекционный угол α_1-5=200º

Измеренные теодолитные углы, отсчёты по КП:

Ст1. Ст5 = 0° Ст2=253°55´ 360°-253°55´=106°05´

Ст2. Ст1 = 0° Ст3=260°34´ 360°-260°34´=99°26´

Ст3 Ст2=0° Ст4=239°12´ 360°-239°12´=120°48´

Измеренные теодолитные углы
Пункты		отсчеты		измеренный угол
станция	точка наблюдения	КП	КЛ
1	5	0°	0°	106° 03´
	2	106° 05´	106° 02´
2	1	0°	0°	99° 03´
	3	99° 26´	99° 23´
3	2	0°	0°	120° 03´
	4	120° 48´	120° 45´
4	3	0°	0°	126° 01´
	5	126° 11´	126° 10´
5	4	0°	0°	87° 03´
	1	87° 35´	87° 32´
				∑=538° 13´

Измерение теодолитных углов производилось со всех пяти станций.

Расчет вычисления координат вершин теодолитного хода.

1. Обработка угловых измерений.

Определяется алгебраическая сумма измеренных углов. Для расчетов пользуемся формулой Σβ_т=180⁰(n-2), где n- это количество измеряемых вершин. В данном случае их 5, соответственно:

Σβ_т=180⁰(n-2)= 180⁰(5-2)=540^о

Выполняем проверку: 106 ^o03'+99 ^o03'+120 ^o03'+126 ^o01'+87 ^o03'=538 ^o13'

Как видно, вычисленное значение не совпадает с теоретическим. Это вызвано тем,что измерения имеют погрешность. Разность алгебраической суммы измеренных углов и теоретических суммы называется фактической невязкой хода (f). Невязка хода рассчитывается по формуле:

f_βф=Σβ_изм – Σβ_т=538 ^o13'- 540 ^o=-1 ^o47'

Величина углов невязка характеризует точность измерений углов. Она не должна превышать предельно допустимой величину:

f_βдоп=1'* =1'* =2'14"

-1 ^o47'≤2'14"

Наша фактическая угловая невязка не превышает допустимую, значит, качество угловых измерений следует признать удовлетворительным. При этом угловые невязку распределяем по измеренным углам полигона равномерно с обратным знаком по формуле:

δ_β=fβф/n=1 ^o47'/5=0,29 0,3

Вычисленные значения вписываем в таблицу, в графу «исправленные горизонтальные углы».

2. Вычисление дирекционных углов.

Используя известный дирекционный угол и значение исправленных горизонтальных углов вычисляются значение дирекционных углов по формуле :

a_n+1=a­_n+180^o – β_n+1 – при условие движения по часовой стрелке, т.е измерены правые углы.

α _1-2=200^o+180^o-106 ^o 23'= 273^o37'

α _2-3=273^o37' +180^o-99^o23'=354^o14'

α _3-4=354^o14'+180^o-120^o23'=53^o51'

α _4-5=53^o51'+180 ^o-126^o28'=107^o23'

Контроль выполняется по той же формуле:

α _5-1= α _5-1+180^o-β₁

α _5-1=107 ^o23'+180 ^o-87^o27'=200^o

3) Вычисление румбов их направлений.

По найденным значениям дирекционных углов производим вычисления румбов. В зависимости от принадлежности дирекционного угла к тому или иному направлению используется 4 формулы:

r= CB: r=б r=ЮB: r=180o- б б1-2=273o37' б2-3=354o14' б3-4=53o21' б4-5=107o23' б5-1=200o

r=ЮЗ: r= б -180o r=СЗ:r=360 o- б rc-з=360o-273o37'=86o23' rc-з=360o-354o14'=5o46' rс-в=53o21' rю-в=180o-107o23' =72o37' rю-з=200 o-180 o=20 o

Определение проложений линий между станциями теодолитного хода. В связи с тем, что рельеф не горизонтальный, поэтому измеренные расстояния между станциями не соответствуют длине проложений между ними.

h

D

d

α

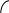
d=D*

cos(2°42')=0.9989

d=D*cos𝛼=25.50*0.9989=25.47 м – проложение между точками 2 и 3

4)Абрис теодолитного хода с измеренными углами и расстояниями между углами.

5) Вычисление приращений координат. При определении приращений координат необходимо учитывать знаки cosr и sinr.

Для этого используется 2 формулы:

∆х=d·cosr ∆х1-2=25,20·cos(86o23')=25,20*0,0590=+1,49 ∆х2-3=25,47·cos(5o46')=25,47*0,9958=+25,36 ∆х3-4=22,24·cos(53o21')=22,24*0,5927=+13,18 ∆х4-5=22,86·cos(72o37')=22,86*0,3027=-6,92 ∆х5-1=34,52·cos(20o)=34,52*0,9397=-32,44

∆y=d·sinr ∆y1-2=25,20*sin(26o23')=25,20*0,9980= -25,15 ∆y2-3= 25,47·sin (5o46') =25,20*0,1005=-2,56 ∆y3-4=22,24·sin(53o21')=22,24*0,8023=+17,84 ∆4-5=22,86·sin(72o37')=22,86*0,9543=+21,82 ∆y5-1=34,52·sin(20o)= 34,52*0,3420=-11,81

6)Вычисление исправленных значений приращений координат.

Данный полигон имеет форму замкнутого многоугольника. В связи с этим теоретическая алгебраическая сумма приращения координат х и у должна равняться нулю по каждой из осей. Однако если вычислить алгебраическую сумму координат, то получится иные значения. Данная разность называется невязкой хода ( f )

Невязка может повлиять на ход работы, поэтому надо определить входит ли она допустимые пределы. Сперва вычисляется абсолютная невязка хода ( f_абс ). Абсолютная невязка показывает, на какую величину разомкнулся полигон.

В нашем случае невязка хода при ∆х f_абс=0,67, а при ∆y f_абс=0,14. Чтобы ее увязать, мы распределили невязку равномерно к значениям с минусом, у нас так и при второй невязки:

∆х4-5=-7,09	∆y1-2=-25,23
∆х5-1=-32,94	∆y5-1=-11,87

Плановое обоснование теодолитного хода.

По исправленным значениям приращения координат х и у, а так же координат начальной точки вычисляются неизвестной координатой точек. Пользуются двумя формулами:

Хn=Xn-1+∆Xn+1исп Х1=200 м Х2=200+1,49=201,49 м Х3=201,49+25,36=226,85 м Х4=226,85+13,18=240,03 м Х5=240,03-7,09=232,94 м Х1=232,94-32,94=200 м

Уn=Уn-1+∆Уn+1исп У1=100 м У2=100-25,23=74,77 У3=74,77-2,56=72,21 У4=72,21+17,85=90,06 У5=90,06+21,82=111,88 У1=111,88-11,88=100

X=232,94 Y=111,88

X=201,49 Y=74,77

						270802
						Плановое обоснование теодолитного хода