24. Атомдардың электрондар арасындағы байланыс түрлері

Элементтердің оптикалық спектрлері толған қабықтардан тыс орналасқан электрондармен анықталады. Өйткені толған қабықтарды құрайтын электрондардың орбиталық және спиндік моменттері бірін-бірі теңгеріп, қорытқы орбиталық және спиндік моменттер нолге тең болады. Сілтілік метал атомдарының бірэлектронды қарапайым конфигурациясына (сыртқы жалғыз электронның n және l-і берілген) екі деңгей ( болғанда ) немесе бір деңгей ( болғанда ) сәйкес келеді. Тұйықталған ішкі қабықтардан тыс екі немесе бірнеше электрон болғанда жағдай едәуір күрделенеді. Егер де электрондар өзара әсерлеспейтін болса, және әрбір электронның спині осы электронның орбиталық моментімен әсерлеспейтін болса, онда берілген электрондық конфигурацияға бір энергия деңгейі сәйкес келген болар еді. Электрондардың өзара әсерлесуінің және әрбір электронның спиндік моментімен оның орбиталық моментінің әсерлесуінің салдарынан берілген электрондық конфигурацияға деңгейлердің бір топ жиынтығы сәйкес келетін болады. Күрделі спектрлерді жүйелегенде берілген электрондық конфигурацияға деңгейлердің бір топ жиынтығы сәйкес келетін болады. Күрделі спектрлерді жүйелегенде берілген электрондық конфигурацияға деңгейлердің дәл қандай жиынтығы сәйкес келетінін, яғни қанша деңгей болады, олар қандай кванттық сандармен сипатталады және олар қалай орналасатынын білу қажет.

Деңгейлердің санын және бұлардың кванттық сандарын анықтау үшін моменттерді векторлық қосудың кванттық заңын пайдалануға болады.

Ескерту: Бірақ эквивалентті, мысалы, р², р³, d², және т.т. электрондар жағдайында бұл әдіс жарамсыз болады да моментердің проекцияларын қосу әдісі қолданылады. және екі момент қана қосылатын бір электрон жағдайынан басқа жағдайларда моменттерді әр түрлі ретпен қосуға болады. Сонда атомдағы әр түрлі әсерлесудің салыстырмалы шамалары қандай болатындығына қарай моментерді белгілі ретпен қосу керек болады.

Жеке электрондардың орбиталық және спиндік моменттерін қосудың әр түрлі екі амалы бар.

1. Электрондардың орбиталық моменттері атомның толық орбиталық моментіне, спиндік моменттері атомның толық моментіне, бұдан кейін және бүтіндей атомның 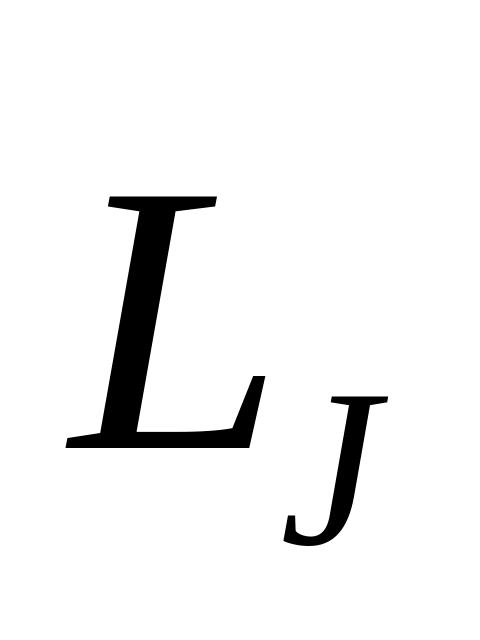толық моментіне қосылады:

, , (1.3.1)

Моменттердің қосудың осы амалы қалыпты (немесе LS-) деп аталатын байланыс жағдайына сәйкес келеді. Байланыстың осы түрі, әдетте, жеңіл және онша ауыр емес атомдарға тән.

Қалыпты байланыс электрондардың өзара электостатикалық әсерлесуі (бұлардың кулондық тебілісі) спин-орбиталық әсерлесумен (спиндық және орбиталық моменттердің магниттік әсерлесуі) салыстырғанда үлкен болғанда орын алады. Электростатикалық әсерлесу энергияның L және S кванттық сандарынан тәуелділігін анықтайды, ал бұған салыстырғанда кіші магниттік әсерлесу – L және S мәндері берілгенде энергияның J кванттық санынан тәуелділігін (мультиплеттік жіктелу) анықтайды.

2. Әрбір электрон үшін оның орбиталық және спиндік моменттері берілген электронның толық моментіне қосылады, бұдан кейін жеке электрондардың толық моменттері атомның толық моментіне қосылады:

, (1.3.2)

Моменттердің осылай қосылуы (jj) байланыс жағдайына сәйкес келеді. (jj) байланыс жеке электронның магниттік спин-орбиталық әсерлесуі әр түрлі электрондардың өзара электростатикалық әсерлесуіне салыстырғанда үлкен болғанда орын алады. Энергия алдымен мәндеріне тәуелді болады, бұдан кейін ғана берілген мәндерінде J мәндеріне тәуелді болады. Мұндай байланыс ауыр атомдарға тән, бірақ өте сирек кездеседі.

Біз қалыпты (немесе LS-) байланыс жағдайындағы моменттерді қосуды қарастырумен шектелеміз. Атомдық жүйенің қосынды орбиталық моменті мына өрнекпен анықталады

, (1.3.3)

мұндағы L қорытқы моменттің орбиталық кванттық саны. Орбиталық моменттері l₁ және l₂ кванттық сандарымен анықталатын екі электроннан тұратын жүйе жағдайында L кванттық саны мына бүтін, оң мәндерді қабылдайды:

, . (1.3.4)

Осыдан L (демек қорытқы момент) немесе әр түрлі мәндерге ие бола алады (екі мәннің кішісін алу керек). Қорытқы орбиталық моменттің қайсыбір Z бағытына проекциясы былай анықталады:

, (1.3.5)

Жүйенің қосынды спиндік моменті (1.3.3)-ке ұқсас анықталады

, (1.3.6)

мұндағы қорытқы спиндік моменттің s кванттық саны электрон санының жұп немесе тақ болуына байланысты бүтін немесе бүтіннің жартысы болуы мүмкін. Егер электронның N саны жұп болса, онда s=Ns, Ns-1,…,0, мұндағы s=1/2, яғни осы жағдайда S-бүтін сандар.

Мысалы, n=4 болғанда s=2,1,0.

Егер электронның N саны тақ болса, онда s барлық бүтіннің жарты мәндерін (Ns-тен s-ке дейінгі, мұндағы s=1/2) қабылдайды. Мысалы, n=5, s=5/2, 3/2 және ½ болады.

және моменттерінің әсерлесуі атомының толық моментін анықтайды:

, (1.3.7)

мұндағы толық J кванттық саны мына мәндердің біреуіне ие болады:

. (1.3.8)

Демек, егер s бүтін болса, (яғни электрондардың саны жұп), онда J бүтін сан болады, егер s бүтіннің жартысы болса (электрондар саны тақ), онда J бүтіннің жартысы болады.

Мысалы:

L	S	J-дің мүмкін мәндері
2	1	3, 2, 1
2	½	5/2, 3/2

Спектрлік белгілеулер. Қалыпты байланыс жағдайында термдер былай белгіленеді: немесе (1.3.9)

мұндағы -мультиплеттілік, J-толық моменттің кванттық саны, -орбиталық кванттық сан мәні бойынша термнің типі (S, P, D және т.т.) анықталады.

Сұрыптау ережелері. Қалыпты байланыс жағдайында L, S және J кванттық сандары үшін мына сұрыптау ережелері тағайындалған:

, , (1.3.10)