33. Шредингер теңдеуі.Стационарлық күйлер.Квантталу. Бір өлшемді потенциалдық шұңқырдағы бөлшек. Сызықтық гармоникалық осциллятор

Э. Шредингер (1926 ж.) – де–Бройльдың заттардың толқындық қасиеттері туралы идеясын ары қарай дамытып, өзінің атымен аталған теңдеуін алды

.

Стационарлық күйлер. Кванттық теорияда ерекше рольді стационарлық күйлер атқарады, бұларда барлық бақыланатын физикалық шамалар уақыт өткенде өзгермейді.

y-функцияның өзі негізінде бақыланбайды. координаттар мен уақытқа байланысты комплекстік функция, ол микробөлшектің күйін сыйпаттайды. Бұл релятивті емес кванттық механиканың негізгі теңдеуі. Стационарлық күйлер үшін ол былай жазылады: . (5,8)

Квантталу. Бордың теориясында квантталу жасанды түрде ендірілген болса, Шредингер теориясында ол өзінен-өзі шығады. Сонда (5.8) теңдеуінің шешімдері ішінен физикалық мағынаға табиғи немесе үлгі (стандарт) шарттарды қанағаттандыратын шешімдері ғана ие болатынын ескеру жеткілікті болады. Осы шарттарды қанағаттандыратын шешімдер Е энергияның кейбір мәндерінде ғана мүмкін болады екен. Бұларды меншікті мәндер деп, ал энергияның осы мәндерінде (5.8) теңдеуінің шешімдері болып табылатын y(r)-функциялары Е-нің меншікті мәндеріне сай меншікті функциялар деп аталады.

Бір өлшемді потенциалдық шұңқырдағы бөлшек Шексіз терең бір өлшемдік потенциалдық шұңқырда орналасқан бөлшектің энергиясының меншікті мәндерін және оларға сәйкес меншікті фунцияларын табайық. Бөлшек тек қана x осі бойымен қозғалсын дейік. Қозғалыс бөлшек үшін өтімсіз қабырғалармен шектелген болсын: x = 0 и x =l. Бұл жағдайда облысында потенциалдық энергия нөлге тең, ал x және x облыстарында шексіздікке тең (36.а-сурет). Шредингер теңдеуі бұл есеп үшін қарапайым түрде былай жазылады:

. (2.9)

Функциясы мына шартты қанағаттандырады

. (2.10)

l- шұңқырдың ені.

Бөлшектің энергиясының меншікті мәндері дискретті болатынын көрсетуге болады: (n = 1, 2, 3, . . .). (2.11)

Сонымен, «қабырғалары» шексіз биік «потенциалдық шұңқырдағы» бөлшек энергиясы тек белгілі дискретті мәндер қабылдай алады, яғни энергия квантталады (36.б -сурет.). Энергияның квантталған мәндері - энергия деңгейлері деп аталынады, ал, n – бөлшектің энергиясының деңгейін анықтайтын бүтін сан негізгі кванттық сан деп аталады.

Массасы m бөлшек х осі бойында бөлшектің тепе-теңдік қалыптан ауытқуына тура пропорционал F=-kx квазисерпімді күш әсерінен қозғалатын болсын. Мұндағы k – серпімділік коэффициенті. Осындай бөлшек сызықтық гармоникалық осциллятор деп аталады.

Гармоникалық осциллятордың потенциалдық энергиясы

Осциллятор үшін Шредингер теңдеуі:

м ұндағы Е – осцилятордың толық энергиясы. Е параметрі мына мәндерді

32. Бір электрондық атомдық жүйелер үшін Шредингер теңдеуі және атомның квантталуы. Энергия деңгейлерінің азғындалу дәрежесі Шредингер теңдеуі. Енді сутегі ядросының кулондық өрісінде электронның күйі жайындағы квант-механикалық есепті шығаруға көшейік. Заряды Ze ядроны координаттар жүйесінің басы деп қабылдаймыз. Сонда потенциалдық энергия сфералық симметриялық тартылыс өрісі (кулондық) түрінде болады:

Гамильтонның классикалық функциясы былайша жазылады: мұндағы m₀ – электрон массасы, P_x, P_y, P_z – импульс құраушылары.

Осы алынған өрнекті Гамильтонның операторына түрлендіреміз:

Осы операторды электронның y толқындық функциясына қолданғанда сутегі атомы үшін Шредингер теңдеуін аламыз:

мұндағы D – Лаплас операторы, Е – электронның толық энергиясы.

z=1 болғанда сутегі атомының энергетикалық деңгейлері үшін өрнек алынады

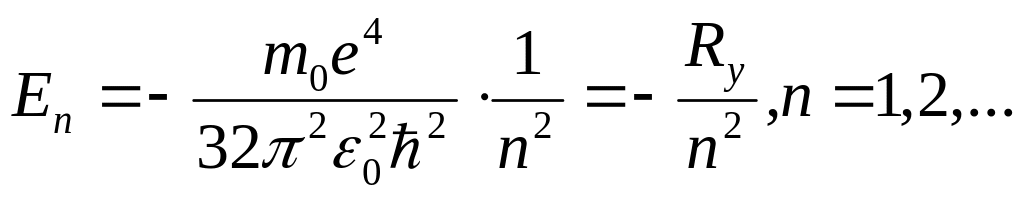(7.8)

R_y=1,79×10^-16 Дж»13,6 эВ.- атомның энергия шкаласының масштабын анықтайды

(7.8) теңдеуіне m кванттық саны енбеген, демек электронның энергия мәні бұған тәуелді емес. Сонда l мәні тұрақты, ал m әр түрлі болатын барлық күйлер (мұндай күйлердің толық саны 2l+1) бірдей энергияға ие болады. Демек бір энергия деңгейіне әртүрлі y-функциялармен бейнеленетін бірнеше күй сәйкес келеді. Осындай энергетикалық деңгейлер айныған, ал нақты энергия мәні бірдей күйлер саны сол энергия деңгейінің азғындалу дәрежесі деп аталады.

31. Сутегі атомының квантталуы. Бір электрондық атомның кванттық сандары және бұлардың физикалық мағынасыСутегі атомында электрон ядроның айналасында Кулондық тартылу күшінің әсерінен радиусы -ге шеңберлік орбитамен қозғалады. Сондықтан электронды осы орбитада ұстап тұратын центрге тартқыш күш электрон мен ядро арасындағы Кулондық күшке тең болады:

.

Импульс моментінің квантталу ережесін ескерсек, алатынымыз:

, мұндағы:

Сутегі атомындағы электронның орбитасы тек дискретті мәндерді қабылдайды, яғни квантталады.

тең болғанда сутегі атомындағы электронның бірінші орбитасының мәні алынады: . Бұл мән бірінші Бор радиусы деп аталады.

Сутегі атомының стационар күйінің энергиясы:

мұндағы: -бас кванттық сан. Бас кванттық сан атом энергиясының деңгейін анықтайды. n=1 атомның негізгі күйі, n>1 атомның қозған күйі деп аталады.

Сутегі атомының энергиясы тек дискретті мәндерді қабылдайды, яғни квантталады.

Кванттық сандар. Шредингер теңдеуінің меншікті функциялары, яғни -функциялар, -үш бүтін санды параметрлермен анықтайды

(1.2.8)

мұндағы n-бас кванттық сан, l-орбиталық, -магниттік кванттық сан деп аталады.

Бас кванттық сан n мәні энергетикалық деңгейдің нөмірімен дәл келеді, атомдағы электронның энергиясын анықтайды және тек бүтін оң мәндер қабылдайды: n=1,2,3,…..

Орбиталық кванттық сан l. Шредингер теңдеуінің шешіміне сәйкес электронның импульс моментінің модулі (механикалық орбиталық момент) мына өрнекпен анықталады:

(1.2.9)

тек дискретті мәндер қабылдай алады, яғни квантталады, l-орбиталық кванттық сан берілген n жағдайында барлығы n мән қабылдайды: l=0,1,2,….n-1.

Магниттік кванттық сан Шредингер теңдеуінің шешіміне сәйкес электронның импульс моментінің қайсыбір Z бағытына мысалы, сыртқы магнит өрісінің проекциясын

(1.2.10)

анықтайды, және атомдағы электронның импульс моментінің векторы кеңістікте квантталып әр түрлі бағдарлана алады (т_е барлығы әр түрлі мән қабылдайды).