56

содержание

1. Основные ПОНЯТИЯ и определения 1

2. Растяжение и сжатие 6

3. Сдвиг и кручение 15

4. Изгиб 20

5. НАПРЯЖЕННОЕ И ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ В ТОЧКЕ И ТЕОРИИ ПРОЧНОСТИ 29

6. Сложное сопротивление 34

7. Прочность при переменных напряжениях 39

8. Элементы теории пластин и оболочек 46

9. Устойчивость стержней 52

1. Основные понятия и определения

Наука, изучающая прочность и надежность элементов конструкций называется сопротивлением материалов.

Основные задачи решаемые в курсе сопротивления материалов:

1. Расчет элементов на прочность (способность элементов сопротивляться разрушению под действием приложенных сил).

2. Расчет на жесткость (способность элементов сопротивляться деформации).

3. Расчет на устойчивость (способность элементов и конструкций сохранять определенную форму равновесия).

Конструктивно элементы конструкций делятся на следующие основные виды (рис.1.1):

1. Брус (стержень) (рис.1.1,а) – тело, у которого два размера малы по сравнению с третьим.

2. Пластина (рис.1.1,б) – тело, ограниченное в основном 2-мя параллельными плоскостями.

3. Оболочка (рис.1.1,в) – тело, ограниченное криволинейными поверхностями, расположенными близко друг от друга.

4. Массив (рис.1.1,г) – тело, у которого все размеры одного порядка.

При решении задач сопротивления материалов вводятся следующие допущения:

1. Материал однороден, т.е. обладает во всех точках одинаковыми свойствами.

2. Материал имеет сплошное строение.

3. Материал изотропен, т.е. обладает во всех направлениях одинаковыми свойствами.

Внутренние силы. Под действием внешних сил элементы конструкции и сами конструкции могут испытывать смещения и изменять свою форму. При этом взаимодействие между частями внутри элемента конструкции характеризуется внутренними силами.

На практике внутренние силы могут характеризовать прочностную надежность детали или конструкции и их определение имеет важное значение.

Для нахождения внутренних сил используется метод сечений, при котором тело мысленно рассекается на 2 части и рассматривается равновесие какой-то части, а действие отброшенной части заменяется действием реакции. На рис.1.2 и рис.1.3 показаны основные типы сил, действующих в сечениях.

Составляющая N называется нормальной или продольной силой и вызывает деформацию растяжения или сжатия. Составляющие перпендикулярны нормалям и стремятся сдвинуть одну часть тела относительно другой. Такие силы называют поперечными. Составляющая М_Z =T скручивает тело и называется крутящим моментом. Моменты М, М_Y, М_X изгибают тело и называются изгибающими моментами.

Для определения внутренних силовых факторов составляются уравнения равновесия отсеченной части тела.

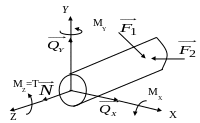
Рис. 1.3. Схемы внутренних и внешних сил для

пространственной расчетной схемы

Частные случаи действия внутренних усилий

1. Действует только продольная сила N (растяжение или сжатие).

1. Действует только поперечная сила Q_X или Q_Y (сдвиг).

2. Действует только М_Z=T (кручение).

3. Действует только изгибающий момент М_X или М_Y (изгиб).

Напряжения и деформации. Для оценки эффективности нагруженности деталей используются такие понятия как напряжение и деформация.

Интенсивность внутренних сил, действующих на элементарной площадке, будем характеризовать нормальным  и касательным  напряжениями (рис.1.4,а).

R_

Рис. 1.4. Схема действия внутренних сил в сечении

Рассмотрим сечение тела А (рис. 1.4,б). В сечении выделим элементарную площадку F. В силу ее малости считаем, что внутренние усилия, приложенные к различным точкам элемента, одинаковы по величине и направлению. Равнодействующей внутренних сил на рассматриваемой площадке будет R, а отношение будет иметь смысл вектора среднего напряжения Р на этой площадке. Переходя к пределу при F0, получаем вектор полного напряжения Р в точке 0, принадлежащей сечению F

.

Разложим силу R на две составляющие – касательную R_, лежащую в плоскости сечения F, и нормальную R_n расположенную перпендикулярно этой плоскости. Вектор полного напряжения Р разлагается на две составляющие – в плоскости сечения и по нормали к сечению. Модули нормального и касательного напряжений равны соответственно

(1.1)

В системе СИ напряжения выражаются в паскалях (1Па=1Н/м²). В технической литературе напряжение часто задают в мегапаскалях

1МПа=10⁶Па=10⁶Н/м²=1Н/мм².

Через любую точку упругого тела, подверженного действию внешней нагрузки можно провести бесчисленное множество сечений, причем в каждом из этих сечений напряжения в точке будут различными. Совокупность напряжений для множества площадок, проходящих через эту точку, определяет напряженное состояние в точке. Для полной характеристики напряженного состояния в точке необходимо знать величину и направление напряжения, а также ориентацию сечения, по которому они действуют (рис.1.5).

Деформацией называется изменение размеров тела. Различают линейную и угловую деформации. В зависимости от свойств тела и величин деформации можно выделить упругие и пластические деформации.

Закон Гука. В расчетах элементов конструкций широко используется закон, впервые сформулированный английским ученым Р. Гуком в конце XVI века: деформации материала элемента в каждой его точке прямо пропорциональны напряжениям в этой же точке.

Область применения закона Гука ограничивается некоторым предельным напряжением, называемым пределом пропорциональности. При напряжении, превышающем предел пропорциональности, линейная зависимость между напряжением и деформацией нарушается, появляется пластическая деформация.

Величину предела пропорциональности, так же как и других напряжений, характеризующих механические свойства материалов, определяют экспериментальными испытаниями образцов.