5.Приклади
1) Довести існування інтеграла
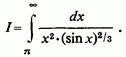
Особливих
точок безліч: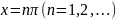
.
У будь-якому кінцевому проміжку їх
кінцеве число, і інтеграл сходиться.
Питання лише про збіжність інтеграла
в нескінченному проміжку.
Маємо:
2) Якщо в збіжний інтеграл
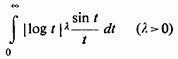
зробити
підстановку
прийдемо до інтеграла
останній,
таким чином, сходиться, незважаючи на
те, що підінтегральна функція при
безмежному зростанні
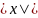коливається між
3) Ми бачили тільки що, що для збіжності інтеграла
(1)
зовсім не потрібно навіть, щоб було
(2)
Довести, що,
(а) якщо існує межа
то - в разі збіжності інтеграла (1) ця межа дорівнює 0; більш того,
(б) якщо існує межа
то і ця межа дорівнює 0
(3)
(в)
якщо інтегрована в проміжку
функція монотонно спадає, то ця умова
(3) необхідно виконується.
Доказ [для (б) і (в)] схоже з доказом аналогічних додатніх рядів.
Відзначимо ще (теж за аналогією з рядами), що навіть для монотонно спадної функції виконання умови (3) не гарантує збіжність інтеграла (1): прикладом може служити розбіжний інтеграл
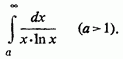
Висновки
Дана курсова робота присвячена особливим прийомам обчислення невласних інтегралів.
У першому пункті наведено деякі чудові інтеграли.
У другому обчислення невласних інтегралів за допомогою інтегральних сум.
У третьму інтеграли Фруллани.
У четвертому інтеграли від ріціональних функцій.
Список використаної літератури
Г.М. Фихтенгольц Курс дифференциального и интегрального исчисления, том II М., Москва, 1969р - 800 с.
І.І. Ляшко, В.Ф. Ємельянов, О.К. Боярчук Математичний аналіз, Підручник: У 2 ч. Ч. I. Вища школа., 1992р . - 495 с.
М.І.Шкіль Математичний аналіз: Підручник. У 2ч. Ч І. – 2-ге вид., перероб. І допов. – К.: Вища школа., 1994 – 423 с.: іл.