Курсовая по физической химии

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

СГТУ, ЭТИ СГТУ (филиал)

КАФЕДРА ФИЗИЧЕСКОЙ И ОРГАНИЧЕСКОЙ ХИМИИ

КУРСОВАЯ РАБОТА

ПО ДИСЦИПЛИНЕ ФИЗИЧЕСКАЯ ХИМИЯ

г.ЭНГЕЛЬС

2010 – 2011г.

Задача №5 (вариант 11)

Указать порядок и найти константу скорости данной реакции, протекающей при заданной температуре Т, пользуясь данными (табл.37) о ходе процесса во времени (с начала реакции).

Реакция	Время	Метод контроля за ходом реакции	Т, К
С12Н22О11 + Н2О С6Н12О6 + С6Н12О6 с – концентрация сахара в данный момент, гмоль/л с0 – начальная концентрация 0,65 , гмоль/л	0	1	298
	1435	1,081
	4315	1,266
	7070	1,464
	11360	1,830
	14170	2,117
	16935	2,466
	19815	2,857
	29925	4,962
		-

Решение:

С₁₂Н₂₂О₁₁ + Н₂О 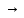С₆Н₁₂О₆ + С₆Н₁₂О₆ - данная реакция протекает по первому порядку, тогда константа скорости находиться по уравнению:

lg

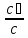
Составим таблицу:

	1435	4315	7070	11360	14170	16935	19815	29925
	1,081	1,266	1,464	1,830	2,117	2,466	2,857
10 – 5	5,41	5,46	5,54	5,32	5,298	5,33	5,299	5,35

Среднее значение константы скорости данной реакции:

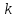= 5,32 10 ^{– 5} моль/лс

Ответ: = 5,32 10 ^{– 5} моль/лс

Задача №6 (вариант 11)

В табл. 38 приведены значения константы скорости k₁ и k₂ реакции при двух различных температурах Т₁ и Т₂ . вычислить энергию активации этой реакции, найти константу скорости при температуре Т₃ и определить, сколько вещества прореагировало к моменту времени 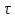, если начальная концентрация вещества с₀ (с₀ – начальные концентрации реагирующих веществ одинаковы). Определить температурный коэффициент скорости реакции и проверить применимость правила Вант – Гоффа на этих примерах. Порядок реакции считать по молекулярности.

Реакция	Т1,К	k1	Т2,К	k2	Т3,К		с0, кмоль/м3
SO2Cl2 SO2 + Cl2	552,2	0,60910-4	593,2	0,132110-2	688,2	35	2,5

Решение:

По уравнению Аррениуса можно найти зависимость константы скорости реакции от температуры: = А

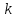где - константа скорости реакции; А – предэкспоненциальный множитель; Е – энергия активации реакции; Т – термодинамическая температура; R – универсальная газовая постоянная.

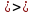ln = ln А ln А = ln +

так как нам дано две температуры составим уравнение для констант скорости и уравняем их:

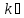ln + = ln+ отсюда находим энергию активации реакции:

Е_а = R ln 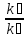подставив данные из таблицы получим:

Е_а = 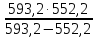ln = 24576 Дж/моль

А = = = 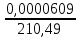2,8910^-7

А при Т₃ = 688,2 К ; = 0,60910^-4 моль/лс

Из уравнения для константы скорости второго порядка найдем количество прореагирующих веществ:

с₀ = 2,5 кмоль/м³ ;=0,58 ч

с = = = 2,5

Правило Вант – Гоффа: k₂ = k₁ = ^{10/(Т₂-Т₁)} = ^0,24 = 2,10

Правило Вант – Гоффа выполняется, так как значение температурного коэффициента лежат в области от 2 до 4.

Ответ: с = 2,5 ; правило Вант – Гоффа выполняется.

Задача № 7 (вариант 12)

Для реакции А, протекающей по n порядку, получены значения константы скорости при различных температурах (табл.39). Рассчитать:

а) энергию активации;

б) предэкспоненциальный множитель;

в) теплоту активации;

г) энтропию активации;

д) температурный коэффициент скорости реакции.

Реакция А	Т,К	К при n=1в с-1 , при n=2в см3-1-1
2HIH2 + I2 n = 2	500	2,93810-6
	510	7,09610-6
	520	1,652 10-5
	530	3,73210-5
	540	8,185 10-5
	550	1,742 10-4
	560	3,606 10-4

Решение:

а) Уравнение Аррениуса: = А

где - константа скорости реакции; А – предэкспоненциальный множитель; Е – энергия активации реакции; Т – термодинамическая температура; R – универсальная газовая постоянная.

Энергию активации можно найти зная хотя бы две константы равновесия и прологарифмировав уравнение Аррениуса : ln = ln А

В координатах ln - 1/Т данная зависимость прямолинейна с тангенсом угла наклона к оси абсцисс равным Е/ R, следовательно E = - tg

Предэкспоненциальный множитель находим по формуле: A = e ^{ln A}

Составим таблицу:

	Т	1/Т	ln
2,93810-6	500	2,00 Е - 03	- 12,7378
7,09610-6	510	1,96 Е – 03	- 11,856
1,652 10-5	520	1,92 Е – 03	- 11,011
3,73210-5	530	1,89 Е – 03	- 10,196
8,185 10-5	540	1,85 Е – 03	- 9,411
1,742 10-4	550	1,82 Е – 03	- 8,655
3,606 10-4	560	1,79 Е - 03	- 7,928

Строим график в координатах ln - 1/Т.

На графике находим а = 0,21 Е – 03 ; в = 6,73

tg- 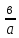= - = - 32048

E_а = - tg = 320488,314 = 266447 Дж/моль (где = 8,314Дж/мольК)

б) ln А = ln + = - 12,7378 + = 51,36

A = e ^{ln A} = 2,718^51,36 = 2 10²² (где е = 2,718)

в) Теплоту активации найдем по формуле для Т = 298 К:

= Е – = 266447 – 8,314298 = 263969Дж/моль

г) Энтропию активации находим =

где h - постоянная Планка (6,62Е – 34 Дж/с);

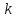- постоянная Больцмана (1,38Е - 23)

n – порядок реакции , n = 2

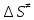= = 8,314 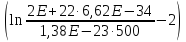= 218,49

д) По правилу Вант – Гоффа найдем температурный коэффициент:

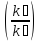= ^{10/(Т₂-Т₁)} = ¹ = 2,33

Ответ: E_а = 266447Дж/моль; A = 2 10²² ; = 263969Дж/моль; = 218,49; 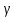=2,33