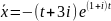§2. Оң жағы квазикөпмүшеліктер болатын сызықтық біртекті емес теңдеудің дара шешімін табу әдісі.
Коэффициенттері тұрақты сызықтық біртекті емес теңдеу қарастырайық:
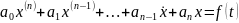
Мұнда
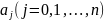нақты
сандар,
–
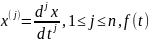қандай да бір
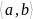аралығында
анықталған және үзіліссіз белгілі
функция.
арлығы тұйық немесе ашық, ақырлы немесе
ақырсыз. Бұл теңдеу қысқаша былай
жазылады:
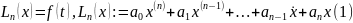
Ал оған сәйкес сызықтық біртекті теңдеу мына түрде болады
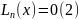
Біртекті (2) теңдеуді шешуге болатыны белгілі. Олай болса тұрақтыны вариациялау әдісін пайдаланып (1) теңдеуді шешуге (жалпы алғанда квадратурада шешуге) болады. Бірақ практикада интеграл алу амалы көбінесе күрделі есептеулерге әкеліп тірейді. Сондықтан квадратурасыз шешілетін, яғни интеграл алу алу амалына әкеліп тіремейтін әдістерді қарастырудың қажеттігі туындайды.
Біз
(1) теңдеудің дара шешімін алгебралық
амалдардың ғана көмегімен табуға мүмкін
болатын жағдайларды қарастырамыз.Табылған
дара шешім мен (2) теңдеудің жалпы
шешімінің қосындысы (1) теңдеудің жалпы
шешімін беретіні белгілі. (1) теңдеудің
оң жағында тұрған
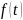функциясы
(қысқаша теңдеудің оң жақ бөлігі)
көпмүшелік пен көрсеткіштік функцияның
көбейтіндісі, яғни
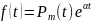
түрінде
болған жағдайды қарастырамыз. Бұл
жағдайда
функциясы көбінесе квазикөпмүшелік
деп
аталады. Мұнда
–
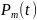коэффициенттері нақты немесе комплекс
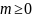дәрежелі көпмүшелік,
–
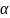нақты немесе комплекс (нөлге тең болуы
да мүмкін) сан.
Сонымен сызықтық біртекті емес
дифференциалдық теңдеуін қарастырамыз. Бұл теңдеудің дара шешімі оның оң жақ бөлігінің түрінен ғана емес, сол жақ бөлігінің түрінен де, атап айтқанда санының
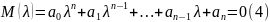
сипаттаушы теңдеуінің түбірі болу–болмауынан, түбірі болса еселігі қандай болатынынан тәуелді.
Дара шешімді құру барысында екі жағдай қарастырамыз.
1–ЖАҒДАЙ.
Көрсеткіштегі
саны
(4) сипаттаушы теңдеудің түбірі емес,
яғни
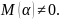
(3) теңдеудің дара шешімін мына түрде
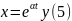
іздейміз. Бұл функцияны (3) теңдеуге апарып қойсақ, бойынша мынадай теңдеу аламыз:
мұндағы
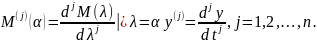
Мынадай белгілеу
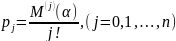
енгізейік.
Әлбетте
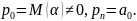Егер
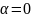болса,
онда
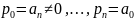болатыны
көрініп тұр. Белгілеуді ескеріп,
(6’)
теңдеуді мына түрде жазамыз:
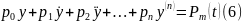
Енді
(6)
теңдеудің
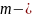дәрежелі бір көпмүшелік түрінде шешімі
болатынын, ол көпмүшеліктің (анықтық
үшін оны
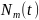деп белгілейік) өзі мен
ретке
дейінгі туындылары үшін мына тепе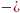
теңдік
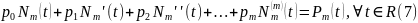
орындалатынын
көрсетелік. Мұнда егер
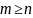болса,
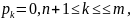ал егер
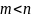болса,
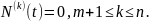
Шынында
да, (6) теңдеудің дара шешімін көпмүшелік
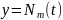түрінде ізделік. Онда (7)
тепе–теңдік
орындалады. Ол теңдікті
ретке дейін дифференциялдап, мынадай
жүйе құралық:
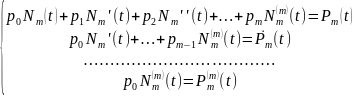
Бұл
үшбұрышты сызықтық біртекті емес
алгебралық жүйе, бұл жүйені Крамер әдісі
бойынша шешеміз. Мұнда
.
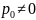Сондықтан
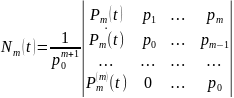
Табылған
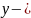тің мәнін (5)
формулаға
апарып қойып,
(3)
теңдеуің
дара шешімін аламыз:
Кейде
(3)
теңдеудің
дара шешімін (9)
түрде
іздейді. Ондағы
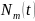көпмүшелігін белгісіз коэффициенттер
арқылы жазады. Ол коэффициенттерді
(9)
функцияны
(3)
теңдеуге
апарып қойып,
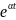көбейткішіне қысқартқаннан кейін
алынатын теңдіктің екі жағындағы
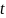айнымалысының бірдей дәрежелері
алдындағы коэффициенттерін теңестіру
арқылы анықтайды. Бұл әдісті анықталмаған
коэффициенттер әдісі деп
атайды. Бірақ бұл әдісті қолдану барысында
(9)
түрдегі
функциядан туындылар алу, оларды теңдеуге
апарып қойғаннан кейін сәйкес
коэффициенттерді жинақтау және ол
коэффициенттер бойынша алынатын
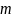
сызықтық теңдеулер жүйесін шешу керек болады. Бұл амалдар ұзақ уақыт алады және оларды орындау барысында техникалық қателер жіберілу мүмкіндігі мол. Ал (8) формула, бұған керісінше, дара шешімнің өзін бірден беріп тұр.
2–ЖАҒДАЙ.
Көрсеткіш
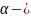саны (4)
сипаттаушы
теңдеудің
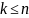еселі түбірі, яғни
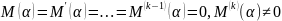
Теңдеудің дара шешімін (5) түрінде іздейміз де,
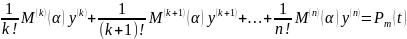
теңдеуін аламыз. Осыған орай (6) теңдеу мына түрде
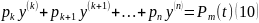
жазылады,
мұндағы
.
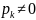Егер
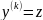белгілеуін енгізсек:
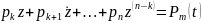
болады. Бұл (6) теңдеу тәріздес теңдеу. Сондықтан (8) формула бойынша оның мынадай
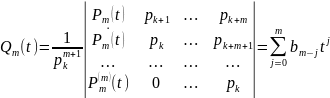
шешімі бар. Бұдан бізге дара шешімді табу жеткілікті болғандықтан,
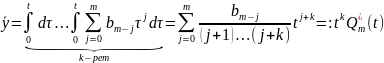
шешімін аламыз. Оны (5) формулаға қойып, (3) теңдеудің дара шешімін
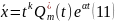
аламыз.
Кейде бұл жағдайда да анықталмаған
коэффициенттер әдісін пайдаланып, (3)
теңдеудің дара шешімін осы (11) түрде
іздейді. Ондағы
көпмүшелігін анықталмаған (белгісіз)
коэффициенттер арқылы жазады. Алайда
жоғарыда айтылған қиындық бұл жағдайда
арта түспесе кемімейді. Себебі бұл
формуланың түрі (9) формулаға қарағанда
күрделірек.
Көрсеткіш
саны сипаттаушы теңдеудің түбірі болатын
екінші жағдай, ол сан түбірі болмайтын
бірінші жағдайды да қамти алады. Ол үшін
бірінші жағдайда
саны сипаттаушы теңдеудің «нөл еселі»
(яғни
)
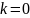түбірі деп алса жеткілікті. Бұл ұғым
саны сипаттаушы теңдеудің түбірі емес
деген жағдайды білдіреді.
Ескерту. Біз (1) теңдеудің оң жағы түріндегі квазикөпмүшелік болған жағдайды қарастырдық. Жалпы жағдайда (1) теңдеудің оң жағы
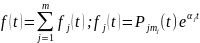
квазикөпмүшелігі
болуы мүмкін. Мұнда
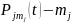- дәрежелі көпмүшеліктер,
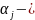өзара тең емес сандар. Бұл жағдайда
әрбір
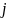үшін
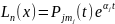
теңдеуінің
дара шешімін табамыз. Олардың қосындысы
суперпозиция қағидасы бойынша
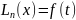теңдеуінің дара шешімін береді.
МЫСАЛДАР.Төмендегі теңдеулердің дара шешімдерін табу керек.
1.
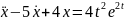сипаттаушы
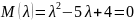теңдеудің екі түбірі бар:
.
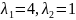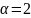сипаттаушы
теңдеудің түбірі емес. Теңдеуге (5)
ауыстыруды енгізсек, алынатын (6) теңдеу
мына түрде болады:
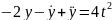,себебі
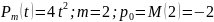
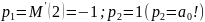
Алынған теңдеудің дара шешімі
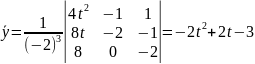
Олай болса, (5) формула бойынша берілген теңдеудің дара шешімі
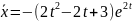
квазикөпмүшелігі болады.
2.
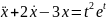сипаттаушы
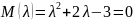теңдеуінің екі түбірі бар:
.
=1
саны сипаттаушы теңдеудің
еселі түбірі болады. Демек
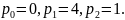(10)
теңдеу мына түрде болады:
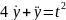
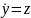
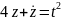
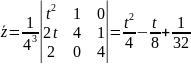
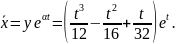
3.
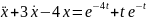теңдеуінің оң жағы екі функцияның
қосындысына тең:
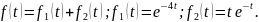
Сондықтан берілген теңдеуді екі жағдайда қарастырып:
1)
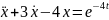
2)
,
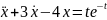соның нәтижесінде алынған теңдеулердің дара шешімдерін табатын болсақ, онда олардың қосындысы берілген теңдеудің дара шешімін береді. Бұл жерде әр қосылғыш функциядағы көрсеткіш саны әр түрлі болғандықтан теңдеуді сол жағдайларға сай, екіге бөліп қарастырып отырғанымызды ескерген жөн.
,
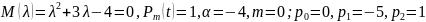
Сондықтан
(5) ауыстырудан кейін,
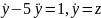белгілеуін енгізсек,
,теңдеуінің дара шешімі:
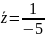
Олай
болса,
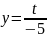болады
да,
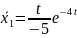бірінші
теңдеудің дара шешімін береді.
,
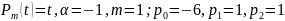
(5)
ауыстырудан
кейін,
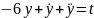
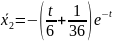
Сонымен берілген теңдеудің дара шешімі:
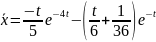
Біз қарастырған мысалдарда көпмүшеліктердің коэффициенттері мен көрсеткіші нақты сандар болды. Ол сандар әлбетте комплекс сандар да бола алады. Сонымен қатар дара шешімді табу барысында олардың нақты немесе комплекс екеніне назар аударғанымыз жоқ. Сондықтан әдістің ол сандар комплекс мәнді болғанда да өз күшін жоймайтыны белгілі.
4.
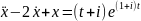теңдеуінің
дара шешімін табу керек.
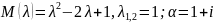сипаттаушы теңдеу түбірі емес. Бұл жерде
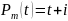. Енді (5) ауыстыру енгізсек,
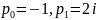болғандықтан,
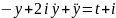теңдеуі алынады. Бұл теңдеудің дара
шешімін (8)
формула бойынша табамыз:
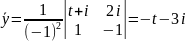
Сондықтан
берілген теңдеудің дара шешімі
