
- •Оглавление
- •Входной контроль
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Модуль 1. Нормативные основы работы эксперта предметной комиссии
- •Модуль 2. Методические рекомендации по оцениванию выполнения заданий с развернутым ответом
- •Вариант 1
- •Вариант 2
- •Пример 1.
- •Пример 2.
- •Пример 3.
- •Контрольные вопросы.
- •Вариант 1
- •Вариант 1
- •Вариант 1
- •Вариант 1
- •Вариант 2
- •Вариант 1
- •Вариант 1
- •Вариант 2
- •Модуль 3. Решение типичных проблемных ситуаций оценивания
- •Модуль 4. Тренинги вариант 1
- •Вариант 2, егэ-2015
- •Вариант 1, работа 1_1. Заполните таблицу своих оценок в баллах
- •Вариант №1, работа 1_2. Заполните таблицу своих оценок в баллах
- •Вариант №1, работа 1_3. Заполните таблицу своих оценок в баллах
- •Задание 19 Вариант №1, работа 1_3.
- •Вариант №1, работа 1_4. Заполните таблицу своих оценок в баллах
- •Вариант №2, работа 2_1. Заполните таблицу своих оценок в баллах
- •Вариант №2, работа 2_2. Заполните таблицу своих оценок в баллах
- •Вариант №2, работа 2_3. Заполните таблицу своих оценок в баллах
- •Вариант №2, работа 2_4. Заполните таблицу своих оценок в баллах
- •Вариант №3, работа 3_1. Заполните таблицу своих оценок в баллах
- •Вариант №3, работа 3_2. Заполните таблицу своих оценок в баллах
- •Вариант №3, работа 3_3. Заполните таблицу своих оценок в баллах
- •Вариант №3, работа 3_4. Заполните таблицу своих оценок в баллах
- •Вариант №4, работа 4_1. Заполните таблицу своих оценок в баллах
- •Вариант №4, работа 4_2. Заполните таблицу своих оценок в баллах
- •Вариант №4, работа 4_3. Заполните таблицу своих оценок в баллах
- •Вариант №4, работа 4_4. Заполните таблицу своих оценок в баллах
- •Модуль 4.
- •Итоговый контроль
ФЕДЕРАЛЬНАЯ СЛУЖБА ПО НАДЗОРУ В СФЕРЕ ОБРАЗОВАНИЯ И НАУКИ
_______________________________________________________________________
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ НАУЧНОЕ УЧРЕЖДЕНИЕ
«ФЕДЕРАЛЬНЫЙ ИНСТИТУТ ПЕДАГОГИЧЕСКИХ ИЗМЕРЕНИЙ»
Унифицированные учебные материалы для подготовки экспертов предметных комиссий ЕГЭ 2016 года
МАТЕМАТИКА
(профильный уровень)
Москва
2016
Унифицированные учебные материалы для подготовки экспертов региональных предметных комиссий ЕГЭ 2016 г. по математике (профильный уровень) предназначены для очной и дистанционной подготовки экспертов по оцениванию заданий с развернутым ответом, которые являются частью контрольных измерительных материалов единого государственного экзамена по математике (профильный уровень).
В учебных материалах дается схематичная информация о нормативных основах работы эксперта предметной комиссии, краткие инструкции по оцениванию выполнения отдельных заданий экзаменационной работы и действиям в типичных проблемных ситуациях оценивания. Материалы содержат вопросы для входного контроля, теоретические и практические задания, а также изображения экзаменационных работ для тренировки в оценивании ответов участников экзамена.
© Федеральный институт педагогических измерений, 2016
Оглавление
Входной контроль 4
Модуль 1. Нормативные основы работы эксперта предметной комиссии 9
Модуль 2. Методические рекомендации по оцениванию выполнения заданий с развернутым ответом 22
Задание 13 (=15 в 2015) 22
Задание 14 (=16 в 2015) 30
Задание 15 (=17 в 2015) 45
Задание 16 (=18 в 2015) 56
Задание 17 (=19 в 2015) 68
Задание 18 (=20 в 2015) 81
Задание 19 (=21 в 2015) 96
Модуль 3. Решение типичных проблемных ситуаций оценивания 108
Модуль 4. Тренинги 115
Итоговый контроль 249
Входной контроль
Ниже представлены четыре варианта входного контроля по математике. Каждый из них состоит из пяти заданий, соответствующих по тематике и уровню сложности заданиям 13-17 в ЕГЭ 2016 г.
При самостоятельной подготовке эксперта выполнять можно один, любой, из этих вариантов. При групповой работе распределение вариантов между экспертами организует и контролирует ответственный за проведение этой работы в конкретной аудитории. Ориентировочное время выполнения входного контроля 70-90 мин.
Вариант 1
1.
а) Решите
уравнение
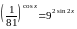 .
.
б) Укажите
корни этого уравнения, принадлежащие
отрезку
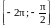 .
.
2.
В правильной
треугольной пирамиде
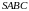 сторона основания
сторона основания
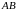 равна 60, а боковое ребро
равна 60, а боковое ребро
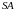 равно 37. Точки
равно 37. Точки
 и
и
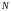 — середины рёбер
и
— середины рёбер
и
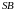 соответственно. Плоскость
соответственно. Плоскость
 содержит прямую
содержит прямую
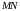 и перпендикулярна плоскости основания
пирамиды.
и перпендикулярна плоскости основания
пирамиды.
а) Докажите,
что плоскость
делит медиану
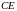 основания в отношении
основания в отношении
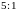 ,
считая от точки
,
считая от точки
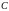 .
.
б) Найдите
расстояние от вершины
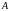 до плоскости
.
до плоскости
.
3.
Решите
неравенство
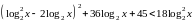 .
.
4.
Точка
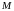 лежит на стороне
лежит на стороне
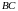 выпуклого четырёхугольника
выпуклого четырёхугольника
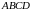 ,
причём
,
причём
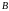 и
— вершины равнобедренных треугольников
с основаниями
и
— вершины равнобедренных треугольников
с основаниями
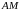 и
и
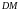 соответственно, а прямые
и
соответственно, а прямые
и
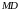 перпендикулярны.
перпендикулярны.
а) Докажите,
что биссектрисы углов при вершинах
и
четырёхугольника
пересекаются на стороне
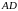 .
.
б) Пусть
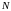 — точка пересечения этих биссектрис.
Найдите площадь четырёхугольника
,
если известно, что
— точка пересечения этих биссектрис.
Найдите площадь четырёхугольника
,
если известно, что
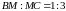 ,
а площадь четырёхугольника,
стороны которого лежат на прямых
,
,
,
а площадь четырёхугольника,
стороны которого лежат на прямых
,
,
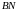 и
и
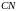 ,
равна 18.
,
равна 18.
5.
Строительство
нового завода стоит 75 млн рублей.
Затраты на производство
 тыс. ед. продукции на таком заводе равны
тыс. ед. продукции на таком заводе равны
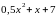 млн рублей в год. Если продукцию
завода продать по цене
млн рублей в год. Если продукцию
завода продать по цене
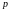 тыс. рублей за единицу,
то прибыль
фирмы (в млн рублей) за один год
составит
тыс. рублей за единицу,
то прибыль
фирмы (в млн рублей) за один год
составит
 .
Когда завод будет построен, фирма будет
выпускать продукцию в таком количестве,
чтобы прибыль была наибольшей. При
каком наименьшем значении
строительство завода окупится не более
чем за 3 года?
.
Когда завод будет построен, фирма будет
выпускать продукцию в таком количестве,
чтобы прибыль была наибольшей. При
каком наименьшем значении
строительство завода окупится не более
чем за 3 года?
Вариант 2
1.
а) Решите
уравнение
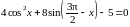 .
.
б) Укажите
корни этого уравнения, принадлежащие
отрезку
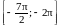 .
.
2.
В основании
четырёхугольной пирамиды
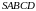 лежит прямоугольник
лежит прямоугольник
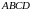 со сторонами
со сторонами
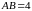 и
и
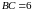 .
Длины боковых рёбер пирамиды
.
Длины боковых рёбер пирамиды
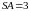 ,
,
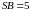 ,
,
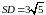 .
.
а) Докажите,
что
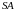 — высота пирамиды.
— высота пирамиды.
б) Найдите
расстояние от вершины
до плоскости
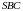 .
.
3.
Решите
неравенство
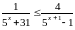 .
.
4. Дан
прямоугольный треугольник
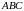 с прямым углом
.
На катете
с прямым углом
.
На катете
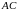 взята точка
.
Окружность с центром
взята точка
.
Окружность с центром
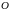 и диаметром
и диаметром
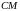 касается гипотенузы в точке
.
касается гипотенузы в точке
.
а) Докажите,
что прямые
и
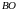 параллельны.
параллельны.
б) Найдите
площадь четырёхугольника
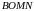 ,
если
,
если
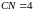 и
и
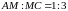 .
.
5. 15-го января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Какую сумму следует взять в кредит, чтобы общая сумма выплат после полного его погашения равнялась 1 млн рублей?
